Topologischer Isolator

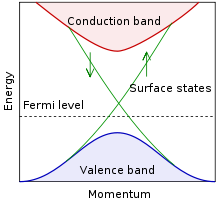Idealisierte elektronische Bandstruktur eines topologischen Isolators. Die Fermi-Energie liegt in der Bandlücke, welche von topologisch geschützten Oberflächenzuständen durchquert wird.

Ein topologischer Isolator ist ein Material welches sich in seinem Inneren als elektrischer Isolator verhält während es gleichzeitig die Bewegung von Ladungen auf seiner Oberfläche erlaubt.

Im Inneren eines topologischen Isolators ähnelt die elektronische Bandstruktur der eines gewöhnlichen Isolators mit der Fermi-Energie zwischen dem Leitungs- und dem Valenzband. Auf der Oberfläche des topologischen Isolators gibt es spezielle Zustände, deren Energie innerhalb der Bandlücke liegt und die Ladungstransport ermöglichen. Die Ladungsträger in diesen Zuständen haben einen Spin welcher senkrecht zu ihrer Bewegungsrichtung ausgerichtet ist. Bei einer gegebenen Energie gibt es nur einen weiteren Zustand mit entgegengesetztem Spin, so dass Streuung stark unterdrückt ist und der Transport an der Oberfläche beinahe dissipationslos ist.^[1] Diese Zustände sind durch einen Index ähnlich dem Geschlecht einer Fläche in der Topologie gekennzeichnet und sind ein Beispiel für einen topologisch geordneten Zustand.^[2]

Topologisch geschützte Randzustände (1D) wurden in Quantentöpfen (sehr dünnen Schichten) von Quecksilbertellurid zwischen Cadmiumtellurid vorhergesagt^[3] und kurz darauf experimentell beobachtet.^[4] Später wurden sie in dreidimensionalen Systemen aus binären Verbindungen mit Bismut vorhergesagt.^[5] Der erste experimentell realisierte dreidimensionale topologische Isolator wurde in Bismut-Antimon beobachtet.^[6] Kurze Zeit später wurden topologisch geschützte Oberflächenzustände auch in reinem Antimon, Bismutselenid, Bismuttellurid und Antimontellurid von verschiedenen Gruppen mittels ARPES nachgewiesen.^[7] Von verschiedenen anderen Materialsystemen wird inzwischen angenommen, dass sie sich wie ein topologischer Isolator verhalten.^[8] In einigen dieser Materialien liegt die Fermi-Energie im Valenz- oder Leitungsband aufgrund natürlich auftretender Defekte. In diesem Fall muss sie mittels Dotierung oder eine Gatterspannung in die Bandlücke geschoben werden.^[9][10]

Ähnliche Randströme treten auch im Quanten-Hall-Effekt auf. Dies erfordert aber große Magnetfelder, tiefe Temperaturen und zweidimensionale Systeme.

Ein helikales Dirac-Fermion, das sich wie ein masseloses relativistisches Teilchen verhält, wurde ebenfalls in einem topologischen Isolator beobachtet.^[11]

Literatur

• Joel Moore: The Birth of Topological Insulators. In: Nature. 464, Nr. 7286, 2010, S. 194. doi:10.1038/nature08916. PMID 20220837.
• C. L. Kane, Mele, E. J.: A New Spin on the Insulating State. In: Science. 314, Nr. 5806, 2006, S. 1692. doi:10.1126/science.1136573. PMID 17170283.
• C.L. Kane: Topological Insulator: An Insulator with a Twist. In: Nature. 4, Nr. 5, 2008, S. 348. doi:10.1038/nphys955.
• Alexandra Witze: Topological Insulators: Physics On the Edge. In: Science News. 2010.
• Geoff Brumfield: Topological insulators: Star material : Nature News. In: Nature. 466, 2010, S. 310-311. doi:doi:10.1038/466310a. Abgerufen am 6. August 2010.
• Shuichi Murakami: Focus on Topological Insulators. In: New Journal of Physics. 2010.

Einzelnachweise

1. ↑ Charles L. Kane, Eugene J. Mele: PHYSICS: A New Spin on the Insulating State. In: Science. 314, Nr. 5806, 2006-12-15, S. 1692-1693. doi:10.1126/science.1136573. Abgerufen am 25. März 2010.
2. ↑ C. L. Kane, Mele, E. J.: Z₂ Topological Order and the Quantum Spin Hall Effect. In: Physical Review Letters. 95, Nr. 14, 30. September 2005, S. 146802. doi:10.1103/PhysRevLett.95.146802.
3. ↑ B. Andrei Bernevig, Taylor L. Hughes, Shou-Cheng Zhang: Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. In: Science. 314, Nr. 5806, 2006-12-15, S. 1757-1761. doi:10.1126/science.1133734. Abgerufen am 25. März 2010.
4. ↑ Markus Konig, Steffen Wiedmann, Christoph Brune, Andreas Roth, Hartmut Buhmann, Laurens W. Molenkamp, Xiao-Liang Qi, Shou-Cheng Zhang: Quantum Spin Hall Insulator State in HgTe Quantum Wells. In: Science. 318, Nr. 5851, 2007-11-02, S. 766-770. doi:10.1126/science.1148047. Abgerufen am 25. März 2010.
5. ↑ Liang Fu, C. L. Kane: Topological insulators with inversion symmetry. In: Physical Review B. 76, Nr. 4, 2007-07-02, S. 045302. doi:10.1103/PhysRevB.76.045302. Abgerufen am 26. März 2010. Shuichi Murakami: Phase transition between the quantum spin Hall and insulator phases in 3D: emergence of a topological gapless phase. In: New Journal of Physics. 9, Nr. 9, 2007, S. 356-356. doi:10.1088/1367-2630/9/9/356. Abgerufen am 26. März 2010.
6. ↑ D. Hsieh, D. Qian, L. Wray, Y. Xia, Y. S. Hor, R. J. Cava & M. Z. Hasan: A Topological Dirac insulator in a 3D quantum spin Hall phase. In: Nature. 452, Nr. 9, 2008, S. 970-974. Abgerufen am 2010.
7. ↑ M. Z Hasan, C. L Kane: Topological Insulators. In: 1002.3895. 2010-02-20. Abgerufen am 27. April 2010.
8. ↑ Hsin Lin, L. Andrew Wray, Yuqi Xia, Suyang Xu, Shuang Jia, Robert J. Cava, Arun Bansil, M. Zahid Hasan: Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. In: Nat Mater. 9, Nr. 7, 2010-07, S. 546-549. doi:10.1038/nmat2771. Abgerufen am 5. August 2010.
9. ↑ D. Hsieh, Y. Xia, D. Qian, L. Wray, F. Meier, J. H. Dil, J. Osterwalder, L. Patthey, A. V. Fedorov, H. Lin, A. Bansil, D. Grauer, Y. S. Hor, R. J. Cava, M. Z. Hasan: Observation of Time-Reversal-Protected Single-Dirac-Cone Topological-Insulator States in Bi2Te3 and Sb2Te3. In: Physical Review Letters. 103, Nr. 14, 2009, S. 146401. doi:10.1103/PhysRevLett.103.146401. Abgerufen am 25. März 2010.
10. ↑ H.-J. Noh, H. Koh, S.-J. Oh, J.-H. Park, H.-D. Kim, J. D. Rameau, T. Valla, T. E. Kidd, P. D. Johnson, Y. Hu and Q. Li: Spin-orbit interaction effect in the electronic structure of Bi2Te3 observed by angle-resolved photoemission spectroscopy. In: EPL Europhysics Letters. 81, Nr. 5, 2008, S. 57006. doi:10.1209/0295-5075/81/57006. Abgerufen am 25. April 2010.
11. ↑ doi:10.1038/nature08234