Winkel-Tripel-Projektion

Winkel-Tripel-Projektion der Erde

Verzerrungen der Winkel-Tripel-Projektion verdeutlicht mit der Tissotschen Indikatrix

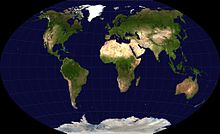
Die Winkel-Tripel-Projektion ist ein 1921 von Oswald Winkel (1874–1953) veröffentlichter Kartennetzentwurf für die gesamte Erdoberfläche.^[1] Sie stellt einen gelungenen Kompromiss zwischen Flächen- und Winkeltreue dar und gehört daher zu den am meisten verwendeten Weltkartenprojektionen. Im Vergleich zur ähnlichen Robinson-Projektion erzielt sie geringere Verzerrungen, gibt dafür jedoch die Lagetreue auf, so dass gekrümmte Breitenkreise entstehen. Im Vergleich zu flächentreuen Projektionen wie der Mollweide-Projektion oder der Eckert-IV-Projektion vermeidet sie deren relativ starke Form- und Winkelverzerrungen, erreicht aber keine vollständige Flächentreue.

Die Projektionsformel ist das arithmetische Mittel aus der rechteckigen Plattkarte und der Aitov-Projektion:

$x = \frac{1}{2}\left[\lambda \cos(\phi_1) + \frac{2 \cos(\phi)\sin\left(\frac{\lambda}{2}\right)}{\mathrm{sinc}(\alpha)}\right]$

$y = \frac{1}{2}\left[\phi + \frac{\sin(\phi)}{\mathrm{sinc}(\alpha)}\right]$

• λ ist der Längengrad (relativ zum Zentralmeridian)
• ϕ ist der Breitengrad
• $\alpha := \arccos\left(\cos(\phi_1) \cos\left(\tfrac{\lambda}{2}\right)\right)$
• ϕ₁ ist der Breitengrad der Standardparallelen der Plattkarte. Winkel wählte für seine Projektion $\phi_1 = \arccos \left( \tfrac 2 \pi \right)$.

Winkel stellte gleichzeitig zwei andere Kartennetzentwürfe vor. Diese werden als Winkel I^[2] (das arithmetische Mittel aus der Plattkarte und der Sinusoidal-Projektion) und Winkel II^[3] bezeichnet. Die Tripelprojektion wird daher auch Winkel III genannt.

Literatur

• Kurt Stüwe: Einführung in die Geodynamik der Lithosphäre. Springer, 2000, ISBN 9783540675167, S. 28 (Eingeschränkte Vorschau in der Google Buchsuche).

Weblink

• Winkel's Tripel Projection. In: Three Modifications for Azimuthal Projections. Carlos A. Furuti, 21. September 2002.
• Winkel Tripel Projection. In: Modified Azimuthal Projections. Carlos A. Furuti, 22. Dezember 2002.
• Beschreibung der inversen Lösung

Einzelnachweise

1. ↑ Oswald Winkel: Neue Gradnetzkombinationen. In: Petermanns Mitteilungen. 67, 1921, S. 248–252.
2. ↑ Deducing the Winkel I and Eckert V Projections. In: A Simple Projection plus Two Derived Works. Carlos A. Furuti, 21. September 2002.
3. ↑ Deducing the Winkel II Projection. In: A Simple Projection plus Two Derived Works. Carlos A. Furuti, 21. September 2002.