Church-Rosser-Theorem

Church-Rosser-Theorem

Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!

Das Church-Rosser-Theorem (benannt nach Alonzo Church und John Barkley Rosser) ist ein Satz aus der Berechenbarkeitstheorie. Es besagt, dass, wenn zwei Terme s und t konversionsäquivalent (bis auf Umbenennung von gebundenen Variablen gleich) sind und für die es eine Reduktion nach s' und t' gibt, dass diese Redukte s' und t' dann zueinander konfluenzäquivalent sind.

Interpretiert man das Lambda-Kalkül als Termersetzungssystem, dann ist das Church-Rosser-Theorem ein Beweis für die Konfluenz im Lambda-Kalkül. Auf der Menge aller Termersetzungssysteme ist Konfluenz unentscheidbar.

Als Konsequenz folgt aus dem Church-Rosser-Theorem, dass jeder Term im Lambda-Kalkül mindestens eine Normalordnungsreduktion besitzt.

Formale Definition

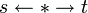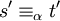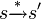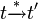Seien s und t zwei Terme im Lambda-Kalkül und s \leftarrow * \rightarrow t , dann existieren s' und t' mit s'\equiv_{\alpha} t' und s \xrightarrow{*} s' und t \xrightarrow{*} t' .

Literatur

  • Alonzo Church, J. Barkley Rosser: Some properties of conversion. In: Transactions of the American Mathematical Society. Band 39, Nr. 3, Mai 1936, Seiten 472-482.
  • Gustav Pomberger, Peter Rechenberg: Informatik Handbuch. Hanser Verlag 2006, ISBN 3446401857, S.84.

Weblinks


Wikimedia Foundation.

Игры ⚽ Нужно сделать НИР?

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Church–Rosser theorem — The Church–Rosser theorem states that if there are two distinct reductions starting from the same lambda calculus term, then there exists a term that is reachable from each reduct via a (possibly empty) sequence of reductions. This is symbolized… …   Wikipedia

  • Satz von Church-Rosser — Das Church Rosser Theorem (bewiesen im Jahr 1936 von Alonzo Church und John Barkley Rosser) ist ein wichtiges Resultat aus der Theorie des Lambda Kalküls. Eine Konsequenz dieses Theorems ist, dass jeder Term des Lambda Kalküls höchstens eine… …   Deutsch Wikipedia

  • Church–Turing thesis — Church s thesis redirects here. For the constructive mathematics assertion, see Church s thesis (constructive mathematics). In computability theory, the Church–Turing thesis (also known as the Church–Turing conjecture, Church s thesis, Church s… …   Wikipedia

  • Alonzo Church — This article is about the mathematician and logician. For the president of the University of Georgia, see Alonzo S. Church. Alonzo Church Alonzo Church (1903–1995) …   Wikipedia

  • J. Barkley Rosser — Infobox Scientist box width = name = John Barkley Rosser image size = caption = birth date = 1907 birth place = death date = 1989 death place = residence = citizenship = USA nationality = USA ethnicity = fields = Mathematical logic Number theory… …   Wikipedia

  • Rosser's trick — For the theorem about the sparseness of prime numbers, see Rosser s theorem. For a general introduction to the incompleteness theorems, see Gödel s incompleteness theorems. In mathematical logic, Rosser s trick is a method for proving Gödel s… …   Wikipedia

  • History of the Church–Turing thesis — This article is an extension of the history of the Church–Turing thesis. The debate and discovery of the meaning of computation and recursion has been long and contentious. This article provides detail of that debate and discovery from Peano s… …   Wikipedia

  • History of the Church-Turing thesis — This article is an extension of the history of the Church Turing thesis.The debate and discovery of the meaning of computation and recursion has been long and contentious. This article provides detail of that debate and discovery from Peano s… …   Wikipedia

  • Abstract rewriting system — In mathematical logic and theoretical computer science, an abstract rewriting system (also (abstract) reduction system or abstract rewrite system; abbreviation ARS) is a formalism that captures the quintessential notion and properties of… …   Wikipedia

  • List of mathematical logic topics — Clicking on related changes shows a list of most recent edits of articles to which this page links. This page links to itself in order that recent changes to this page will also be included in related changes. This is a list of mathematical logic …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”