Co-RP (Komplexitätsklasse)
- Co-RP (Komplexitätsklasse)
-
co-RP (random polynominal) bzw. co-RP(ε(n)) bezeichnet die Klasse der Entscheidungsprobleme, für die es einen randomisierten Algorithmus mit polynomineller maximaler Rechenzeit gibt, der jede zu akzeptierende Eingabe mit Wahrscheinlichkeit 1 annimmt und für jede nicht zu akzeptierende Eingabe der Länge n eine durch ε(n) beschränkte Fehlerwahrscheinlichkeit hat.
Dieser Fehlertyp wird als einseitiger Fehler (one-sided error) bezeichnet, im Gegensatz zu dem zweiseitigen Fehler (two-sided error) bei der Komplexitätsklasse BPP.
Geht man von der Sprache co-L zum Komplement L über, so erhält man die Komplexitätsklasse RP.
Die Klasse co-RP liegt zwischen den Klassen ZPP (= RP 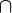 co-RP) und BPP, es gilt also ZPP ⊆ co-RP ⊆ BPP.
co-RP) und BPP, es gilt also ZPP ⊆ co-RP ⊆ BPP.
Außerdem gilt RP ⊆ NP und co-RP ⊆ co-NP.
Literatur
- Wegener, Ingo. Komplexitätstheorie: S.31-34
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Komplexitätsklasse P — In der Komplexitätstheorie ist P (auch: PTIME) diejenige Komplexitätsklasse, welche die Entscheidungsprobleme enthält, die in Polynomialzeit für deterministische Turingmaschinen lösbar sind. Diese Problemklasse wird allgemein als die Klasse der… … Deutsch Wikipedia
Komplexitätsklasse NP — NP (nichtdeterministisch polynomielle Zeit) ist eine Komplexitätsklasse aus dem Bereich der Komplexitätstheorie. Sie bezeichnet die Klasse aller Entscheidungsprobleme, die von einer nichtdeterministischen Turingmaschine bezüglich der Eingabelänge … Deutsch Wikipedia
Komplexitätsklasse — Zusammenhang verschiedener Komplexitätsklassen Eine Komplexitätsklasse ist in der Komplexitätstheorie eine Kategorie von Problemen beziehungsweise von Algorithmen, zusammengefasst nach einem gemeinsamen Maß der Komplexität. Definiert wird eine… … Deutsch Wikipedia
BQP (Komplexitätsklasse) — Die Komplexitätsklasse BQP (bounded error quantum polynomial time) ist ein Begriff aus der Komplexitätstheorie, einem Teilgebiet der Theoretischen Informatik. Zu BQP gehören alle Probleme, die auf einem Quantencomputer in Polynomialzeit mit einer … Deutsch Wikipedia
P (Komplexitätsklasse) — In der Komplexitätstheorie ist P (auch: PTIME) diejenige Komplexitätsklasse, welche die Entscheidungsprobleme enthält, die in Polynomialzeit für deterministische Turingmaschinen lösbar sind. Diese Problemklasse wird allgemein als die Klasse der… … Deutsch Wikipedia
SL (Komplexitätsklasse) — In der Komplexitätstheorie bezeichnet L die Klasse der Entscheidungsprobleme, welche von einer deterministischen Turingmaschine mit logarithmischem Platzverbrauch gelöst werden können. Um logarithmischen Platzverbrauch definieren zu können, muss… … Deutsch Wikipedia
Co-NP (Komplexitätsklasse) — Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung. In der Komplexitätstheorie bezeichnet Co NP eine Komplexitätsklasse … Deutsch Wikipedia
PH (Komplexitätsklasse) — Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung. Die Polynomialzeithierarchie (PH, auch: polynomielle Hierarchie)… … Deutsch Wikipedia
NP (Komplexitätsklasse) — NP (nichtdeterministisch polynomielle Zeit) ist in der Informatik eine Komplexitätsklasse aus dem Bereich der Komplexitätstheorie. Sie bezeichnet die Klasse aller Entscheidungsprobleme, die von einer nichtdeterministischen Turingmaschine… … Deutsch Wikipedia
RP (Komplexitätsklasse) — RP (random polynomial) bzw. RP( (n)) bezeichnet die Klasse der Entscheidungsprobleme, für die es einen randomisierten Algorithmus A mit polynomieller Laufzeit gibt, der jede nicht zu akzeptierende Eingabe mit Wahrscheinlichkeit 1 ablehnt und für… … Deutsch Wikipedia
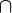 co-RP) und BPP, es gilt also ZPP ⊆ co-RP ⊆ BPP.
co-RP) und BPP, es gilt also ZPP ⊆ co-RP ⊆ BPP.