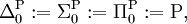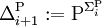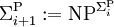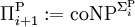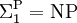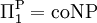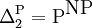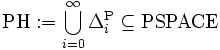PH (Komplexitätsklasse)

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Die Polynomialzeithierarchie (PH, auch: polynomielle Hierarchie) ist die vermutete Struktur von Komplexitätsklassen zwischen NP und PSPACE. Der Grundgedanke hinter der Polynomialzeithierarchie ist die Frage, ob durch die Hinzunahme von Orakeln, die Leistungsfähigkeit einer Turingmaschine gesteigert werden kann.

Orakel-Turingmaschine

Orakel sind Erweiterungen einer Turingmaschine. Eine Turingmaschine mit Orakel A (wobei A eine Sprache ist), kann in einem Schritt entscheiden, ob ein Wort w zu A gehört oder nicht.

Symbolisch wird eine solche Konstruktion wie folgt dargestellt:

• B^A bedeutet, dass eine Turingmaschine M mit L(M) = B ein Orakel A befragt.

Mit Blick auf Komplexitätsklassen ergibt sich die folgende Notation:

• P^NP (sprich: "P hoch NP") ist die Menge aller Probleme, die sich von einer Turingmaschine entscheiden lassen, die in Abhängigkeit von der Eingabelänge nur polynomiellen Zeitverbrauch aufweist, zur Lösung jedoch ein Orakel benutzen kann, das in der Lage ist, ein Problem aus NP zu entscheiden.

Mathematische Definition

Die Polynomialzeithierarchie wird mit Hilfe der drei Symbole Δ_i, Σ_i und Π_i definiert.

Für diese Symbole gilt:

$\Delta_0^{\rm P} := \Sigma_0^{\rm P} := \Pi_0^{\rm P} := \mbox{P},$

wobei P die Menge aller in Polynomialzeit lösbaren Entscheidungsprobleme ist. Für i ≥ 0 definiert man

$\Delta_{i+1}^{\rm P} := \mbox{P}^{\Sigma_i^{\rm P}}$

$\Sigma_{i+1}^{\rm P} := \mbox{NP}^{\Sigma_i^{\rm P}}$

$\Pi_{i+1}^{\rm P} := \mbox{coNP}^{\Sigma_i^{\rm P}}$

Es gilt also insbesondere:

$\Sigma_1^{\rm P}=\mbox{NP}$

$\Pi_1^{\rm P}=\mbox{coNP}$

$\Delta_2^{\rm P}=\mbox{P}^{\mbox{NP}}$

Eigenschaften

Anders als zunächst vermutet, können sich durch die Polynomialzeithierarchie nicht alle Komplexitätsklassen abbilden lassen. Zwar ist die genaue Struktur der Hierarchie weiterhin unbekannt, jedoch konnte sich bereits folgender Sachverhalt beweisen lassen:

• $\mbox{PH} := \bigcup_{i=0}^{\infty} \Delta_i^{\rm P} \subseteq \mbox{PSPACE}$

Ob PH = PSPACE gilt, ist bis heute unbekannt.

Zudem weiß man, dass im Falle der Gleichheit von P und NP die Polynomialzeithierarchie kollabiert, d.h. es gilt:

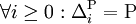$\forall i\geq 0 : \Delta_i^{\rm P} = \mbox{P}$ (Analog auch für Σ_i und Π_i)

oder allgemeiner:

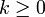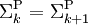• Falls für ein $k\geq 0$ gilt: $\Sigma_k^{\rm{P}}=\Sigma_{k+1}^{\rm{P}}$, so gilt für alle i > k: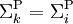 $\Sigma_k^{\rm{P}}=\Sigma_{i}^{\rm{P}}$

• In der deskriptiven Komplexitätstheorie beschreibt die Logik zweiter Stufe die Polynomialzeithierarchie.

Literatur

Michael Sipser: Introduction to the Theory of Computation. 2. Auflage. ISBN 053494728X.