- Cocktailsort
-
Der Begriff Shakersort bezeichnet einen stabilen Sortieralgorithmus, der eine Menge von linear angeordneten Elementen (z. B. Zahlen) der Größe nach sortiert. Weitere Namen für diesen Algorithmus sind Cocktailsort, Shearsort oder BiDiBubbleSort (bidirektionales Bubblesort).
Inhaltsverzeichnis
Prinzip
Das zu sortierende Feld wird abwechselnd nach oben und nach unten durchlaufen. Dabei werden jeweils zwei benachbarte Elemente verglichen und gegebenenfalls vertauscht.
Durch diese Bidirektionalität kommt es zu einem schnellerem Absetzen von großen bzw. kleinen Elementen. Anhand des Sortierverfahrens lässt sich auch der Name erklären, denn der Sortiervorgang erinnert an das Schütteln des Arrays oder eines Barmixers.
Komplexität
Der Algorithmus besitzt eine quadratische und daher im Vergleich zu vielen anderen Sortieralgorithmen schlechte Worst-Case-Laufzeit, die jedoch in der einfachen Version gleichzeitig auch der normalen Laufzeit entspricht. In der Informatik drückt man dies mittels Landau-Symbol durch
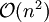 aus. Dafür bietet dieser Algorithmus den Vorteil eines geringen Speicherbedarfes. Da der Algorithmus ein In-place-Verfahren ist, braucht er keinen zusätzlichen Speicher.
aus. Dafür bietet dieser Algorithmus den Vorteil eines geringen Speicherbedarfes. Da der Algorithmus ein In-place-Verfahren ist, braucht er keinen zusätzlichen Speicher.Beispiel
Eine Reihe von sechs Zahlen soll aufsteigend sortiert werden. Die fett markierten Zahlenpaare werden verglichen. Wenn die rechte Zahl hierbei kleiner ist als die linke, so werden die Zahlen vertauscht (blau markiert).
55 07 78 12 42 33 1. Durchlauf 07 55 78 12 42 33 07 55 78 12 42 33 07 55 12 78 42 33 07 55 12 42 78 33 07 55 12 42 33 78 2. Durchlauf 07 55 12 33 42 78 07 55 12 33 42 78 07 12 55 33 42 78 07 12 55 33 42 78 3. Durchlauf 07 12 55 33 42 78 07 12 33 55 42 78 07 12 33 42 55 78 4. Durchlauf 07 12 33 42 55 78 07 12 33 42 55 78 5. Durchlauf 07 12 33 42 55 78 Fertig sortiert.
Implementierungen
Ruby
def bidibubblesort!(arr) t = arr.size - 1 for i in 1..arr.size for j in (i-1)..arr.size-1-i if (arr[t-j] < arr[t-(j+1)]) arr[t-j], arr[t-(j+1)] = arr[t-(j+1)], arr[t-j] end if (arr[j] > arr[j+1]) arr[j], arr[j+1] = arr[j+1], arr[j] end end end endJava 5
static <E extends Comparable<E>> void shakerSort(E[] sammlung) { boolean austausch; int links = 1; // Start beim zweiten Element int rechts = sammlung.length-1; int fertig = rechts; do { austausch = false; for (int ab = rechts; ab >= links; ab--) { // abwärts if (sammlung[ab].compareTo(sammlung[ab-1]) < 0) { austausch = true; fertig = ab; final E temp = sammlung[ab-1]; sammlung[ab-1] = sammlung[ab]; sammlung[ab] = temp; } } links = fertig + 1; for (int auf = links; auf <= rechts; auf++) { // aufwärts if (sammlung[auf].compareTo(sammlung[auf-1]) < 0) { austausch = true; fertig = auf; final E temp = sammlung[auf-1]; sammlung[auf-1] = sammlung[auf]; sammlung[auf] = temp; } } rechts = fertig - 1; } while (austausch); }
C# (C Sharp)
* * ACHTUNG: Der Algorithmus erzeugt eine NullReferenceException, wenn ein * Element des Arrays null ist! */ /// <summary> /// Sortiert das angegebene Array mit dem ShakerSort-Algorithmus. /// </summary> /// <param name="array">Das zu sortierende Array.</param> /// <param name="reverse">Bestimmt, ob die Liste absteigend sortiert werden /// soll.</param> public static void ShakerSort<T>(T[] array, bool reverse) where T : IComparable<T> { if(array == null || array.Length < 2) return; int count = array.Length; bool changed = true, oddpass = true; while (changed) { changed = false; if (oddpass) { oddpass = false; for (int i = 1; i < count; i++) // aufwärts { int j = array[i].CompareTo(array[i - 1]); if ((j < 0 && !reverse) || (j > 0 && reverse)) { T tmp = array[i]; array[i] = array[i - 1]; array[i - 1] = tmp; changed = true; } } } else { oddpass = true; for (int i = count - 1; i > 0; i--) // abwärts { int j = array[i].CompareTo(array[i - 1]); if ((j < 0 && !reverse) || (j > 0 && reverse)) { T tmp = array[i]; array[i] = array[i - 1]; array[i - 1] = tmp; changed = true; } } } } }Visual Basic
Sub ShakerSort(ByRef Feld() As Integer) Dim Size As Integer Dim Half As Integer Dim Temp As Integer Dim I, J As Integer Size = UBound(Feld) + 1 'Größe des Arrays +1 Half = Size / 2 For I = 1 To Half For J = 1 To UBound(Feld) - I 'aufwärts If Feld(J) > Feld(J + 1) Then Temp = Feld(J) Feld(J) = Feld(J + 1) Feld(J + 1) = Temp End If Next J For J = UBound(Feld) To 1 + I Step -1 'abwärts If Feld(J - 1) > Feld(J) Then Temp = Feld(J) Feld(J) = Feld(J - 1) Feld(J - 1) = Temp End If Next J Next I End SubAls Ergänzung sollte erwähnt werden, dass nach dem ersten Schleifendurchlauf das größte Element hinten (bzw. vorn) steht, nach dem zweiten das kleinste ganz vorn (bzw. hinten). Somit lässt sich der Algorithmus verbessern, indem zwei Variablen benutzt werden, um die Grenzen von rechts und links zusammenzuschieben. Dadurch läuft der Algorithmus gegen die Mitte der Liste.
Weblinks
Wikimedia Foundation.
