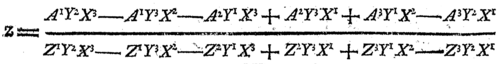Cramersche Regel

Die cramersche Regel oder Determinantenmethode ist eine mathematische Formel für die Lösung eines linearen Gleichungssystems. Sie ist bei der theoretischen Betrachtung linearer Gleichungssysteme hilfreich. Für die Berechnung einer Lösung ist der Rechenaufwand jedoch in der Regel zu hoch, da dabei verhältnismäßig viele Determinanten auftreten. Deshalb kommen dazu andere Verfahren aus der numerischen Mathematik zum Einsatz. Die cramersche Regel geht zurück auf Gabriel Cramer, der sie im Jahr 1750 veröffentlichte.

Regel

Ausgangspunkt für die cramersche Regel ist ein lineares Gleichungssystem (LGS) mit Koeffizientenmatrix A und rechter Seite b, also in der Form^[1]

Ax = b,

das genau so viele Gleichungen wie Unbekannte hat (A ist quadratisch) und eindeutig lösbar ist. Die eindeutige Lösbarkeit ist genau dann gegeben, wenn

$det(A)\neq0$.

In diesem Fall ist die Lösung x eindeutig bestimmt, durch

$x_i = \frac{\det(A_i)}{\det(A)}$ für alle i.

Die Matrix A_i wird gebildet, indem die i-te Spalte der Koeffizientenmatrix A durch die rechte Seite des Gleichungssystems b ersetzt wird.

Beispiele

Lineares Gleichungssystem 2. Ordnung

Diesem Beispiel liegt das folgende lineare Gleichungssystem zu Grunde:

$\begin{matrix} \color{blue}{1}\,\color{black}x_1+\color{blue}{2}\,\color{black}x_2=\color{OliveGreen}{3}\\ \color{blue}{4}\,\color{black}x_1+\color{blue}{5}\,\color{black}x_2=\color{OliveGreen}{6} \end{matrix}$

Die erweiterte Koeffizientenmatrix des Gleichungssystems ist dann:

$\begin{pmatrix}\color{blue}{A} & \color{OliveGreen}b\end{pmatrix} = \left(\begin{array}{cc|c} \color{blue}{1} & \color{blue}{2} & \color{OliveGreen}{3} \\ \color{blue}{4} & \color{blue}{5} & \color{OliveGreen}{6} \end{array}\right)$

Nach der cramerschen Regel berechnet sich dessen Lösung wie folgt:

$x_1 = \frac{\det(A_1)}{\det(A)} = \frac{\begin{vmatrix}\color{OliveGreen}{3}&\color{blue}{2}\\ \color{OliveGreen}{6}&\color{blue}{5}\end{vmatrix}} {\begin{vmatrix}\color{blue}{1}&\color{blue}{2}\\ \color{blue}{4}&\color{blue}{5}\end{vmatrix}} = \frac{3}{-3} = -1\qquad$

$x_2 = \frac{\det(A_2)}{\det(A)} = \frac{\begin{vmatrix}\color{blue}{1}&\color{OliveGreen}{3}\\ \color{blue}{4}&\color{OliveGreen}{6}\end{vmatrix}} {\begin{vmatrix}\color{blue}{1}&\color{blue}{2}\\ \color{blue}{4}&\color{blue}{5}\end{vmatrix}} = \frac{-6}{-3} = 2$

Die senkrechten Striche sind eine gebräuchliche Notation der Determinante.

Lineares Gleichungssystem 3. Ordnung

Diesem Beispiel liegt das folgende lineare Gleichungssystem zu Grunde:

$\begin{matrix} \color{blue}{82}\,\color{black}x_1+\color{blue}{45}\,\color{black}x_2+\color{blue}{9}\,\color{black}x_3=\color{OliveGreen}{1}\\ \color{blue}{27}\,\color{black}x_1+\color{blue}{16}\,\color{black}x_2+\color{blue}{3}\,\color{black}x_3=\color{OliveGreen}{1}\\ \color{blue}{9}\,\color{black}x_1+\color{blue}{5}\,\color{black}x_2+\color{blue}{1}\,\color{black}x_3=\color{OliveGreen}{0}\\ \end{matrix}$

Die erweiterte Koeffizientenmatrix des Gleichungssystems ist dann:

$\begin{pmatrix}\color{blue}{A} & \color{OliveGreen}b\end{pmatrix} = \left(\begin{array}{ccc|c} \color{blue}{82} & \color{blue}{45} & \color{blue}{9} & \color{OliveGreen}{1} \\ \color{blue}{27} & \color{blue}{16} & \color{blue}{3} & \color{OliveGreen}{1} \\ \color{blue}{9} & \color{blue}{5} & \color{blue}{1} & \color{OliveGreen}{0} \end{array}\right)$

Nach der cramerschen Regel berechnet sich die Lösung des Gleichungssystems wie folgt:

$x_1 = \frac{\det(A_1)}{\det(A)} = \frac{\begin{vmatrix}\color{OliveGreen}{1} &\color{blue}{45} &\color{blue}{9} \\ \color{OliveGreen}{1} &\color{blue}{16} &\color{blue}{3} \\ \color{OliveGreen}{0} &\color{blue}{5} &\color{blue}{1} \end{vmatrix}} {\begin{vmatrix}\color{blue}{82} &\color{blue}{45} &\color{blue}{9} \\ \color{blue}{27} &\color{blue}{16} &\color{blue}{3} \\ \color{blue}{9} &\color{blue}{5} &\color{blue}{1} \end{vmatrix}} = \frac{1}{1} = 1\qquad$

$x_2 = \frac{\det(A_2)}{\det(A)} = \frac{\begin{vmatrix}\color{blue}{82} &\color{OliveGreen}{1} &\color{blue}{9} \\ \color{blue}{27} &\color{OliveGreen}{1} &\color{blue}{3} \\ \color{blue}{9} &\color{OliveGreen}{0} &\color{blue}{1} \end{vmatrix}} {\begin{vmatrix}\color{blue}{82} &\color{blue}{45} &\color{blue}{9} \\ \color{blue}{27} &\color{blue}{16} &\color{blue}{3} \\ \color{blue}{9} &\color{blue}{5} &\color{blue}{1} \end{vmatrix}} = \frac{1}{1} = 1\qquad$

$x_3 = \frac{\det(A_3)}{\det(A)} = \frac{\begin{vmatrix}\color{blue}{82} &\color{blue}{45} &\color{Olive Green}{1} \\ \color{blue}{27} &\color{blue}{16} &\color{OliveGreen}{1} \\ \color{blue}{9} &\color{blue}{5} &\color{OliveGreen}{0} \end{vmatrix}} {\begin{vmatrix}\color{blue}{82} &\color{blue}{45} &\color{blue}{9} \\ \color{blue}{27} &\color{blue}{16} &\color{blue}{3} \\ \color{blue}{9} &\color{blue}{5} &\color{blue}{1} \end{vmatrix}} = \frac{-14}{1} = -14$

Die senkrechten Striche sind eine gebräuchliche Notation der Determinante.

Geschichte

Die cramersche Regel wurde 1750 von Gabriel Cramer im Anhang 1 seines Buchs „Introduction à l′analyse des lignes courbes algébriques“ ^[2] veröffentlicht. Er gab darin explizit die Formeln für lineare Gleichungssysteme mit bis zu drei Gleichungen an und beschrieb, wie man die Lösungsformeln für Gleichungssysteme mit mehr Gleichungen erstellen kann. Da die Determinante noch nicht eingeführt war, verwendete er Brüche mit je einem Polynom im Zähler und Nenner. Wie der folgende Auszug aus der Originalarbeit zeigt, sind diese mit den Polynomen der Leibniz-Formel identisch.

An diesem Beispiel sieht man auch, dass Cramer noch nicht die heutige Notation linearer Gleichungssysteme verwendete. Mit dieser lautet die Formel wie folgt:

$x_1 = \frac{b_1a_{22}a_{33} - b_1a_{32}a_{23} - b_2a_{12}a_{33} + b_2a_{32}a_{13} + b_3a_{12}a_{23} - b_3a_{22}a_{13}}{a_{11}a_{22}a_{33} - a_{11}a_{32}a_{23} - a_{21}a_{12}a_{33} + a_{21}a_{32}a_{13} + a_{31}a_{12}a_{23} - a_{31}a_{22}a_{13}}$

Cramer selbst war bewusst, dass lineare Gleichungssysteme nicht immer eindeutig lösbar sind.^[3] Étienne Bézout zeigte dann 1764, dass der Nenner null wird, wenn das Gleichungssystem nicht eindeutig lösbar ist.^[3] Des Weiteren gab Cramer keinen Beweis für seine Formel an. Diesen lieferte erst Augustin Louis Cauchy im Jahr 1815. Dabei führte er auch die heutzutage verwendete Notation der cramerschen Regel ein.

Gottfried Wilhelm Leibniz brachte die cramersche Regel schon 1678 in einem Manuskript zu Papier. Dieses wurde allerdings erst später entdeckt und hatte somit keine Auswirkung auf die Entwicklung von Lösungsverfahren für lineare Gleichungssysteme.^[3] Colin Maclaurin beschrieb in seinem Werk „Treatise of Algebra“ die Spezialfälle der cramerschen Regel für lineare Gleichungssysteme aus zwei oder drei Gleichungen. Er hatte zwar die Idee, diese Formeln auf Gleichungssysteme mit mehreren Gleichungen zu erweitern, doch im Gegensatz zu Cramer fand er keine Regel, wie man die Vorzeichen in den dabei verwendeten Polynomen richtig setzt.^[4] Im 20. Jahrhundert entfachte Carl Benjamin Boyer einen Streit unter Mathematik-Historikern, ob Maclaurin oder Cramer der Entdecker der Formel war. Er empfahl dabei auch eine Umbenennung in Maclaurin-Cramer-Regel.^[5]

Rechenaufwand

Um mit der cramerschen Regel ein lineares Gleichungssystem mit n Unbekannten zu lösen, müssen n + 1 Determinanten berechnet werden. Die Anzahl der auszuführenden arithmetischen Operationen hängt damit allein vom Algorithmus zur Berechnung der Determinanten ab.

Werden die Determinanten wie von Cramer mit Hilfe der Leibniz-Formel berechnet, so sind für jede Determinante $(n-1) \cdot n!$ Multiplikationen und n! − 1 Additionen notwendig. Schon bei einem System aus vier Gleichungen sind 360 Multiplikationen, vier Divisionen und 115 Additionen notwendig. Im Vergleich zu anderen Verfahren sind dies sehr viele Operationen. Auch unter Verwendung effizienter Algorithmen zur Determinantenberechnung ist der Rechenaufwand für die Lösung eines linearen Gleichungssystems mit der cramerschen Regel wesentlich höher als beispielsweise beim gaußschen Eliminationsverfahren.

Bei der Berechnung einer $n \times n$-Matrix auf einem Rechner mit 10⁸-Gleitpunktoperationen pro Sekunde (100 Mflops) würden sich die folgenden Rechenzeiten ergeben^[6]:

n	10	12	14	16	18	20
Rechenzeit	0.4s	1m	3.6h	41 Tage	38 Jahre	16 000 Jahre

Beweis

Für diesen Beweis verwendet man eine Matrix X_i, die entsteht, indem man die i-te Spalte der Einheitsmatrix durch den Lösungsvektor x des Gleichungssystems Ax = b ersetzt. So sieht X₂ für ein Gleichungssystem mit vier Gleichungen folgendermaßen aus:

$X_2 = \begin{pmatrix}1 & x_1 & 0 & 0 \\ 0 & x_2 & 0 & 0 \\ 0 & x_3 & 1 & 0 \\ 0 & x_4 & 0 & 1\end{pmatrix}$

Anhand dieses Beispiels lässt sich auch sehen, dass AX_i = A_i gilt.

$\begin{align} A \cdot X_2 &= \begin{pmatrix}a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44}\end{pmatrix} \cdot \begin{pmatrix}1 & x_1 & 0 & 0 \\ 0 & x_2 & 0 & 0 \\ 0 & x_3 & 1 & 0 \\ 0 & x_4 & 0 & 1\end{pmatrix} \\ &= \begin{pmatrix}a_{11} & a_{11}x_1 + a_{12}x_2 + a_{13}x_3 + a_{14}x_4 & a_{13} & a_{14} \\ a_{21} & a_{21}x_1 + a_{22}x_2 + a_{23}x_3 + a_{24}x_4 & a_{23} & a_{24} \\ a_{31} & a_{31}x_1 + a_{32}x_2 + a_{33}x_3 + a_{34}x_4 & a_{33} & a_{34} \\ a_{41} & a_{41}x_1 + a_{42}x_2 + a_{43}x_3 + a_{44}x_4 & a_{43} & a_{44}\end{pmatrix} \\&= \begin{pmatrix}a_{11} & b_1 & a_{13} & a_{14} \\ a_{21} & b_2 & a_{23} & a_{24} \\ a_{31} & b_3 & a_{33} & a_{34} \\ a_{41} & b_4 & a_{43} & a_{44}\end{pmatrix} \\&= A_2 \end{align}$

Da zusätzlich det(X_i) = x_i gilt, folgt mit der Produktregel für Determinanten

$\begin{matrix} \det(A) & \cdot & \det(X_i) & = & \det(A_i)\\ \det(A) & \cdot & x_i & = & \det(A_i)\\ & & x_i & = & \det(A_i) \cdot \det(A)^{-1} \end{matrix}$

Da die Determinante det(A) nach Voraussetzung nicht das Null-Element ist, existiert det(A) ^{− 1}.

Verallgemeinerung

Eine Verallgemeinerung der cramerschen Regel stellt der folgende Satz dar: Gegeben sei ein quadratisches lineares Gleichungssystem (LGS) der Form

Ax = b.

Ist $x=(x_1,x_2,\ldots,x_n)$ eine Lösung des LGS, dann gilt

$\det(A) \cdot x_i = \det(A_i)$ für jedes i.

Die Matrix A_i entsteht aus der Koeffizientenmatrix, indem die i-te Spalte der Matrix A durch die rechte Seite des Gleichungssystems b ersetzt wird.

Es entfällt die Einschränkung auf ein eindeutig lösbares Gleichungssystem. Da zudem keine Division mehr auftritt, gilt der Satz für alle Gleichungssysteme mit Koeffizienten aus einem kommutativen Ring.^[7] Diese Verallgemeinerung wird nicht mehr cramersche Regel genannt.

Folgerungen aus der cramerschen Regel

Die Inverse einer Matrix

Hauptartikel: Reguläre Matrix

Die einzelnen Spalten der Inversen einer Matrix A werden jeweils von der Lösung des Gleichungssystems Ax = e_j mit dem j-ten Einheitsvektor auf der rechten Seite gebildet. Berechnet man diese mit der cramerschen Regel, so erhält man unter Verwendung der Adjunkten $\operatorname{adj} (A)$ die Formel

$A^{-1} = \frac{\operatorname{adj} (A)}{\det(A)}$

Diese Formel zeigt auch eine Eigenschaft von Matrizen mit Einträgen aus einem kommutativen Ring anstatt einem Körper. Diese sind demnach genau dann invertierbar, wenn det(A) invertierbar ist.

Lösung eines homogenen linearen Gleichungssystems

Mit Hilfe der cramerschen Regel lässt sich einfach zeigen, dass die triviale Lösung $x_1 = x_2 = \ldots = x_n = 0$ die einzige Lösung eines jeden homogenen linearen Gleichungssystems mit $\det(A) \ne 0$ ist. Da bei allen Matrizen A_i in der i-ten Spalte nur Nullen stehen, sind deren Spalten nicht mehr linear unabhängig, und es gilt deshalb det(A_i) = 0. Damit berechnen sich alle x_i zu null.

Aus der obigen Eigenschaft folgt direkt, dass der Kern eines linearen Gleichungssystems Ax = b mit $\det(A) \ne 0$ der Nullvektor ist und dieses deshalb eindeutig lösbar ist.

Einzelnachweise

1. ↑ Die Koeffizienten müssen Elemente eines Körpers sein.
2. ↑ Gabriel Cramer: Introduction à l’analyse des lignes courbes algébriques. Genf 1750, S. 657–659.
3. ↑ ^{a b c} Jean-Luc Chabert et al.: A History of Algorithms. Form the Pebble to the Microchip. Springer-Verlag, 1999, ISBN 3-540-63369-3, S. 284–287 (Dieses Buch enthält eine englische Übersetzung von Cramers Originalveröffentlichung.).
4. ↑ Antoni A. Kosinski: Cramer's Rule Is Due to cramer. In: Mathematics Magazine. Bd. 74, Nr. 4, Oktober 2001, S. 310–312.
5. ↑ Bruce A. Hedman: An Earlier Date for „Cramer’s Rule“ In: Historica Mathematica. Bd. 24, 1999, S. 365–368.
6. ↑ W. Dahmen, A. Reusken: Numerik für Ingenieure und Naturwissenschaftler, Springer, 2006, ISBN 3-540-25544-3
7. ↑ Serge Lang: Algebra. 2. Auflage. Addison-Wesley, 1984, ISBN 0-201-05487-6, S. 451.