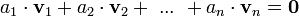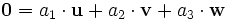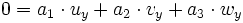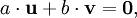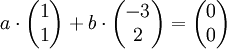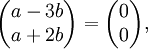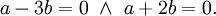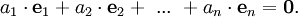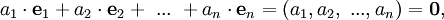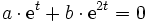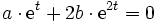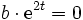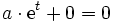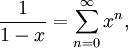- Linear unabhängig
-
In der linearen Algebra wird eine Familie von Vektoren eines Vektorraums linear unabhängig genannt, wenn sich der Nullvektor nur durch eine Linearkombination der Vektoren erzeugen lässt, in der alle Koeffizienten der Kombination auf den Wert Null gesetzt werden. Man kann zeigen, dass diese Bedingung dazu äquivalent ist, dass sich keiner der Vektoren als Linearkombination der anderen darstellen lässt. Andernfalls heißen sie linear abhängig. Die Bezeichnung „linear voneinander abhängig“ ist unpräzise, da diese fälschlicherweise suggeriert, dass jeder der beteiligten Vektoren sich durch die anderen darstellen lässt.
Zum Beispiel sind im dreidimensionalen Euklidischen Raum
 die Vektoren (1,0,0), (0,1,0) und (0,0,1) linear unabhängig. Die Vektoren (2, − 1,1), (1,0,1) und (3, − 1,2) sind hingegen nicht linear unabhängig, denn der dritte Vektor ist die Summe der beiden ersten, d.h. die Summe der ersten beiden minus den dritten ergibt den Nullvektor. Die Vektoren (1,2, − 3), ( − 2, − 4,6) und (1,1,1) sind wegen
die Vektoren (1,0,0), (0,1,0) und (0,0,1) linear unabhängig. Die Vektoren (2, − 1,1), (1,0,1) und (3, − 1,2) sind hingegen nicht linear unabhängig, denn der dritte Vektor ist die Summe der beiden ersten, d.h. die Summe der ersten beiden minus den dritten ergibt den Nullvektor. Die Vektoren (1,2, − 3), ( − 2, − 4,6) und (1,1,1) sind wegen 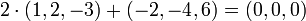 ebenfalls linear abhängig; jedoch ist hier der dritte Vektor nicht als Linearkombination der beiden anderen darstellbar.
ebenfalls linear abhängig; jedoch ist hier der dritte Vektor nicht als Linearkombination der beiden anderen darstellbar.Inhaltsverzeichnis
Definition
Es sei V ein Vektorraum über dem Körper K und I eine Indexmenge. Eine durch I indizierte Familie
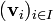 heißt linear unabhängig, wenn jede hierin enthaltene endliche Teilfamilie linear unabhängig ist.
heißt linear unabhängig, wenn jede hierin enthaltene endliche Teilfamilie linear unabhängig ist.Eine endliche Familie
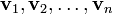 von Vektoren aus V heißt linear unabhängig, wenn die einzig mögliche Darstellung des Nullvektors als Linearkombination
von Vektoren aus V heißt linear unabhängig, wenn die einzig mögliche Darstellung des Nullvektors als Linearkombinationmit Koeffizienten
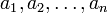 aus dem Grundkörper K diejenige ist, bei der alle Koeffizienten ai gleich Null sind. Lässt sich dagegen der Nullvektor auch nichttrivial (mit Koeffizienten ungleich Null) erzeugen, dann sind die Vektoren linear abhängig.
aus dem Grundkörper K diejenige ist, bei der alle Koeffizienten ai gleich Null sind. Lässt sich dagegen der Nullvektor auch nichttrivial (mit Koeffizienten ungleich Null) erzeugen, dann sind die Vektoren linear abhängig.Die Familie
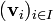 ist also linear abhängig genau dann, wenn es Koeffizienten
ist also linear abhängig genau dann, wenn es Koeffizienten 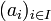 gibt, von denen fast alle, aber nicht alle gleich 0 sind, so dass
gibt, von denen fast alle, aber nicht alle gleich 0 sind, so dassAchtung: Der Nullvektor
 ist ein Element des Vektorraumes V, während 0 ein Element aus dem Körper K ist!
ist ein Element des Vektorraumes V, während 0 ein Element aus dem Körper K ist!Andere Charakterisierungen und einfache Eigenschaften
- Die Vektoren
 sind genau dann linear unabhängig, wenn sich keiner von ihnen als Linearkombination der anderen darstellen lässt.
sind genau dann linear unabhängig, wenn sich keiner von ihnen als Linearkombination der anderen darstellen lässt.
Diese Aussage gilt nicht im allgemeineren Kontext von Moduln über Ringen.
- Eine Variante dieser Aussage ist das Abhängigkeitslemma: Sind
 linear unabhängig und
linear unabhängig und  linear abhängig, so lässt sich
linear abhängig, so lässt sich 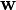 als Linearkombination von
als Linearkombination von  schreiben.
schreiben.
- Ist eine Familie von Vektoren linear unabhängig, so ist jede Teilfamilie dieser Familie ebenfalls linear unabhängig. Ist eine Familie hingegen linear abhängig, so ist jede Familie, die diese abhängige Familie beinhaltet, ebenso linear abhängig.
- Elementare Umformungen der Vektoren verändern die lineare Abhängigkeit oder die lineare Unabhängigkeit nicht.
- Die Anzahl der linear unabhängigen Vektoren in einer Familie von Vektoren
 entspricht dem Rang der Matrix
entspricht dem Rang der Matrix 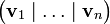 . Durch Hinzufügen und Entfernen eines Vektors und Vergleich des Rangs der Matrizen, kann die lineare Abhängigkeit eines Vektors von einer beliebigen Familie geprüft werden.
. Durch Hinzufügen und Entfernen eines Vektors und Vergleich des Rangs der Matrizen, kann die lineare Abhängigkeit eines Vektors von einer beliebigen Familie geprüft werden.
Bedeutung
Lineare Gleichungssysteme
In einer Linearkombination sind die Koeffizienten eindeutig bestimmt, wenn die Vektoren
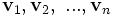 linear unabhängig sind. Dies kann zur Feststellung der Lösbarkeit von linearen Gleichungssystemen benutzt werden. Das lineare Gleichungssystem ist genau dann eindeutig lösbar, wenn die Spaltenvektoren der Koeffizientenmatrix linear unabhängig sind.
linear unabhängig sind. Dies kann zur Feststellung der Lösbarkeit von linearen Gleichungssystemen benutzt werden. Das lineare Gleichungssystem ist genau dann eindeutig lösbar, wenn die Spaltenvektoren der Koeffizientenmatrix linear unabhängig sind.Die Überprüfung, ob zum Beispiel drei Vektoren aus
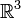 linear unabhängig sind, entspricht dem Lösen eines linearen Gleichungssystems. Dazu wird aus
linear unabhängig sind, entspricht dem Lösen eines linearen Gleichungssystems. Dazu wird ausein homogenes lineares Gleichungssystem gebildet:
und mittels des gaußschen Eliminationsverfahrens nach a1,a2,a3 gelöst. Gibt es nur eine einzige Lösung, nämlich dass a1 = a2 = a3 = 0, dann sind die Vektoren linear unabhängig. Existieren weitere Lösungen, sind sie linear abhängig.
Basen
Wichtig ist das Konzept der linearen Unabhängigkeit in Bezug auf die Basis eines Vektorraums. Eine Basis ist ein linear unabhängiges Erzeugendensystem. Basen erlauben es, in beliebigen Vektorräumen mit Koordinaten zu rechnen.
Beispiele
Beispiel 1: einzelner Vektor
Der Vektor
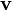 sei ein Element des Vektorraums V über K. Dann ist der einzelne Vektor
sei ein Element des Vektorraums V über K. Dann ist der einzelne Vektor 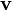 für sich genau dann linear unabhängig, wenn gilt, dass
für sich genau dann linear unabhängig, wenn gilt, dass 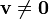 (d.h. ungleich dem Nullvektor ist).
(d.h. ungleich dem Nullvektor ist).Denn aus der Definition des Vektorraums folgt, dass wenn
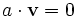 mit
mit 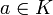 ,
, 
nur a = 0 oder
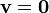 sein kann!
sein kann!Beispiel 2: zwei bestimmte Vektoren in
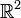
Die Vektoren
 und
und 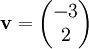 sind in
sind in 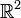 linear unabhängig.
linear unabhängig.Beweis: für
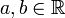 gelte
gelted.h.
Dann gilt
also
Dieses Gleichungssystem ist nur für die Lösung a = 0, b = 0 (die sogenannte triviale Lösung) erfüllt; d.h. u und v sind linear unabhängig.
Beispiel 3: „natürliche“ Basis in
Im Vektorraum
 betrachte folgende Elemente (die natürliche oder Standard-Basis von V):
betrachte folgende Elemente (die natürliche oder Standard-Basis von V):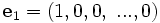

- ...
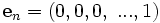
Dann ist die Vektorfamilie
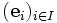 mit
mit 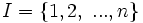 linear unabhängig.
linear unabhängig.Beweis: Für
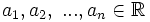 gelte
gelteDann gilt aber auch
und daraus folgt, dass ai = 0 für alle
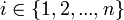 .
.Beispiel 4: Funktionen als Vektoren
Sei V der Vektorraum aller Funktionen
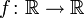 . Die beiden Funktionen et und e2t in V sind linear unabhängig.
. Die beiden Funktionen et und e2t in V sind linear unabhängig.Beweis: Es seien
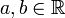 und es gelte
und es geltefür alle
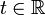 . Leitet man diese Gleichung nach t ab, dann erhält man eine zweite Gleichung
. Leitet man diese Gleichung nach t ab, dann erhält man eine zweite GleichungIndem man die erste von der zweiten Gleichung subtrahiert, erhält man
Da diese Gleichung für alle t und damit insbesondere auch für t = 0 gelten muss, folgt daraus durch Einsetzen von t = 0, dass b = 0 sein muss. Setzt man das so berechnete b wieder in die erste Gleichung ein, dann ergibt sich
Daraus folgt wieder, dass (für t = 0) a = 0 sein muss.
Da die erste Gleichung nur für a = 0 und b = 0 lösbar ist, sind die beiden Funktionen et und e2t linear unabhängig.
Siehe auch: Wronski-Determinante
Beispiel 5: Reihen
Sei V der Vektorraum aller reellwertigen stetigen Funktionen
 auf dem offenen Einheitsintervall. Dann gilt zwar
auf dem offenen Einheitsintervall. Dann gilt zwaraber dennoch sind
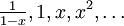 linear unabhängig. Linearkombinationen aus Potenzen von x sind nämlich nur Polynome und keine allgemeinen Potenzreihen, insbesondere also in der Nähe von 1 beschränkt, so dass sich
linear unabhängig. Linearkombinationen aus Potenzen von x sind nämlich nur Polynome und keine allgemeinen Potenzreihen, insbesondere also in der Nähe von 1 beschränkt, so dass sich 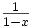 nicht als Linearkombination von Potenzen darstellen lässt.
nicht als Linearkombination von Potenzen darstellen lässt.Beispiel 6: Zeilen und Spalten einer Matrix
Interessant ist auch die Frage, ob die Zeilen einer Matrix linear unabhängig sind oder nicht. Dabei werden die Zeilen als Vektoren betrachtet. Falls die Zeilen einer quadratischen Matrix linear unabhängig sind, so nennt man die Matrix regulär, andernfalls singulär. Die Spalten einer quadratischen Matrix sind genau dann linear unabhängig, wenn die Zeilen linear unabhängig sind. Beispiel einer Folge von regulären Matrizen: Hilbert-Matrix.
Beispiel 7: Rationale Unabhängigkeit
Zahlen aus
 , die sich nicht als Linearkombinationen mit Zahlen aus
, die sich nicht als Linearkombinationen mit Zahlen aus  darstellen lassen nennt man rational unabhängig oder inkommensurabel (siehe auch Inkommensurabilität (Mathematik)). Die Zahlen
darstellen lassen nennt man rational unabhängig oder inkommensurabel (siehe auch Inkommensurabilität (Mathematik)). Die Zahlen 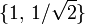 sind rational unabhängig, oder inkommensurabel. Die Zahlen
sind rational unabhängig, oder inkommensurabel. Die Zahlen 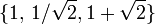 sind rational abhängig.
sind rational abhängig.Verallgemeinerung
Der Begriff der linearen Unabhängigkeit lässt sich weiter zu einer Betrachtung von unabhängigen Mengen verallgemeinern, siehe dazu Matroid.
Wikimedia Foundation.