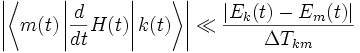- Adiabatensatz
-
Der Adiabatensatz der Quantenmechanik sagt, dass wenn sich der Hamiltonoperator H(t) eines Systems (zum Beispiel aufgrund äußerer Einflüsse) „langsam genug“ ändert, in guter Näherung der Zustand des Systems
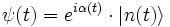 im Verlauf der adiabatischen Evolution im n-ten Eigenzustand von H(t) verbleibt.
im Verlauf der adiabatischen Evolution im n-ten Eigenzustand von H(t) verbleibt.„Langsam genug“ bedeutet (für
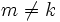 ), dass
), dassgilt.
Dabei ist ΔTkm die charakteristische Zeit des Übergangs des Systems vom Zustand
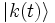 in den Zustand
in den Zustand 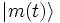 und Ek(t) und Em(t) sind die zu den Zuständen k und m gehörenden Energie-Eigenwerte des Systems.
und Ek(t) und Em(t) sind die zu den Zuständen k und m gehörenden Energie-Eigenwerte des Systems.Das bedeutet, dass die Änderung von H(t) langsam ist im Vergleich zur natürlichen Zeitskala des Systems, die durch Übergänge zwischen den energetischen Eigenzuständen definiert wird.
Im adiabatischen Limit sind die Änderungen von H(t) infinitesimal langsam:
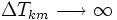 und damit folgt:
und damit folgt: 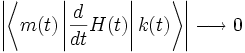 .
.
Inhaltsverzeichnis
Beispiele in der Physik
Das wohl bekannteste Beispiel in der Physik ist wohl die Born-Oppenheimer-Näherung. Max Born und Robert Oppenheimer konnten zeigen, dass für die Berechnung der Zustandsänderungen der Elektronen eines Moleküls, die Bewegung der Atomkerne (die Änderung von H(t)) vernachlässigt werden kann. Einfach ausgedrückt, die Elektronen bewegen sich so schnell und die Zeit die sie für einen Übergang zwischen zwei Elektronenniveaus brauchen ist so kurz, dass die Bewegung der (langsamen) Atomkerne für eine Berechnung keine Rolle spielt.
Geschichte
Das Adiabatische Theorem der Quantenmechanik geht zurück auf Arbeiten von Max Born und Wladimir Alexandrowitsch Fock aus dem Jahr 1928. Eine vollständige mathematische Formulierung gelang jedoch erst Tosio Kato (1950) im Zusammenhang mit der Störungstheorie linearer Operatoren.
Literatur
- Born, M.; Fock, V. Beweis des Adiabatensatzes 1928
- Kato, T. On the Adiabatic Theorem of Quantum Mechanics J. Phys. Soc. Jap. 5, 435-439 1950
- Buslaev, V.S.; Grinina, E.A. Remarks on the quantum adiabatic theorem St. Petersburg Math. J. 16, 639-648 2005 und darin angegebene Referenzen
Siehe auch
Wikimedia Foundation.