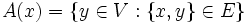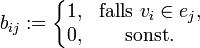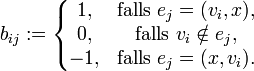- Adjazenzmatrix (Graphentheorie)
-
Für die Repräsentation von Graphen im Computer gibt es im wesentlichen zwei gebräuchliche Formen, die Adjazenzmatrix und die Adjazenzliste. Alternative Bezeichnungen sind Nachbarschaftsmatrix und Nachbarschaftsliste. Die Bedeutung der beiden Begriffe liegt darin, dass praktisch jede algorithmische Lösung graphentheoretischer Probleme auf wenigstens eine der beiden Repräsentationen zurückgreift. Eine weitere, aber seltener genutzte Möglichkeit zur Darstellung von Graphen im Computer ist die Inzidenzmatrix, die man auch als Knoten-Kanten-Matrix bezeichnet.
Inhaltsverzeichnis
Adjazenzmatrix (Nachbarschaftsmatrix)
Ein Graph mit n Knoten kann durch eine
 -Matrix repräsentiert werden. Dazu nummeriert man die Knoten von 1 bis n durch und trägt in die Matrix die Beziehungen der Knoten zueinander ein.
-Matrix repräsentiert werden. Dazu nummeriert man die Knoten von 1 bis n durch und trägt in die Matrix die Beziehungen der Knoten zueinander ein.Ungerichteter Graph Adjazenzmatrix 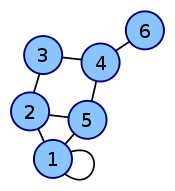
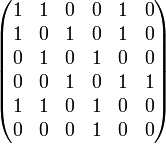
In ungerichteten Graphen ohne Mehrfachkanten wird in die i-te Zeile und j-te Spalte eine 1 eingetragen, wenn der i-te und j-te Knoten benachbart, d.h. durch eine Kante verbunden sind. Andernfalls wird eine 0 eingetragen. Da die Relation „benachbart“ symmetrisch ist (wenn Knoten i mit Knoten j benachbart ist, dann ist auch Knoten j mit Knoten i benachbart), ist auch die Adjazenzmatrix symmetrisch.
In gerichteten Graphen ohne Mehrfachkanten wird in die i-te Zeile und j-te Spalte eine 1 eingetragen, wenn der i-te Knoten Vorgänger des j-ten Knoten ist. Andernfalls wird eine 0 eingetragen. Die Matrix ist genau dann symmetrisch, wenn es der Graph ist und ihre Hauptdiagonale enthält nur Nullen, wenn der Graph schleifenfrei ist. Dies ist genau der Grund, warum man gerichtete Graphen, die symmetrisch und schleifenfrei sind, auch ungerichtet nennt. Ihre Adjazenzmatrix ist dann nämlich äquivalent zu der eines ungerichteten Graphen, und diese sind ein Spezialfall der gerichteten Graphen.
In Graphen mit Mehrfachkanten trägt man in die i-te Zeile und j-te Spalte die Vielfachheit von {i,j} in ungerichteten Graphen bzw. (i,j) in gerichteten Graphen ein. Auch an dieser Stelle sieht man leicht, warum Graphen ohne Mehrfachkanten als Spezialfälle von Graphen mit Mehrfachkanten betrachtet werden können.
In kantengewichteten Graphen trägt man häufig auch das Kantengewicht der jeweiligen Kante ein, wobei in Abhängigkeit vom betrachteten Problem Knoten, die nicht durch eine Kante verbunden sind, mit 0 oder ∞ markiert werden. (Siehe auch: Entfernungstabelle)
Hypergraphen lassen sich nicht durch eine Adjazenzmatrix darstellen.
Adjazenzliste (Nachbarschaftsliste)
Die Adjazenzliste wird in ihrer einfachsten Form durch eine einfach verkettete Liste aller Knoten des Graphen dargestellt, wobei jeder Knoten eine Liste aller seiner Nachbarn (in ungerichteten Graphen) bzw. Nachfolger (in gerichteten Graphen) besitzt. Vielfachheiten der Kanten, Knotengewichte, und Kantengewichte werden meist in Attributen der einzelnen Elemente gespeichert. Je nach Problemstellung kann es notwendig sein, statt einer einfach verketteten Liste eine doppelt verkettete Liste zu verwenden und in gerichteten Graphen zusätzlich zur Liste der Nachfolger eine Liste der Vorgänger zu verwalten.
Definition: Sei
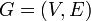 ein Graph und
ein Graph und 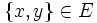
Inzidenzmatrix
Ein Graph mit n Knoten und m Kanten kann auch durch eine
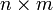 -Matrix repräsentiert werden. Dazu nummeriert man die Knoten von 1 bis n und die Kanten von 1 bis m durch und trägt in die Matrix die Beziehungen der Knoten zu den Kanten ein.
-Matrix repräsentiert werden. Dazu nummeriert man die Knoten von 1 bis n und die Kanten von 1 bis m durch und trägt in die Matrix die Beziehungen der Knoten zu den Kanten ein.Jede Spalte der Inzidenzmatrix enthält genau zwei von Null verschiedene Einträge. In ungerichteten Graphen zweimal die 1 und in schleifenfreien gerichteten Graphen einmal die 1 (Endknoten) und einmal die − 1 (Startknoten).
Für einen ungerichteten Graphen G = (V,E) mit V = {v1,...,vn} und E = {e1,...,em} ist die Inzidenzmatrix B = (bi,j) formal also definiert durch:
Für einen schleifenfreien, gerichteten Graphen G = (V,E) mit V = {v1,...,vn} und E = {e1,...,em} ist die Inzidenzmatrix B = (bi,j) definiert durch:
wobei x hier einen beliebigen Knoten darstellt.
Einen Anwendungsfall stellt die Inzidenzmatrix eines Petri-Netzes dar.
Beispiel
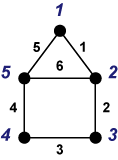
Der im Bild dargestellte Graph hat beispielsweise die folgende Inzidenzmatrix. Die Zahlen an den Kanten sind dabei nicht mit Gewichtungen der Kanten zu verwechseln. Sie beschreiben die Namen der Kanten (m1,m2,...,m6) die in der Matrix als Spalten wiederzufinden sind.
Vergleichende Betrachtungen zwischen Adjazenzmatrix und Adjazenzliste
Adjazenzlisten sind zwar aufwändiger zu implementieren und zu verwalten, bieten aber eine Reihe von Vorteilen gegenüber Adjazenzmatrizen. Zum einen verbrauchen sie stets nur linear viel Speicherplatz, was insbesondere bei dünnen Graphen (also Graphen mit wenig Kanten) von Vorteil ist, während die Adjazenzmatrix quadratischen Platzbedarf bezüglich der Anzahl Knoten besitzt (dafür aber kompakter bei dichten Graphen, also Graphen mit vielen Kanten ist). Zum anderen lassen sich viele graphentheoretische Probleme nur mit Adjazenzlisten in linearer Zeit lösen. In der Praxis verwendet man daher meist diese Form der Repräsentation.
Wikimedia Foundation.