Einfach verkettete Liste

Verkettete Listen gehören zu den dynamischen Datenstrukturen, die eine Speicherung von einer im Vorhinein nicht bestimmten Anzahl von miteinander in Beziehung stehenden Werten einfacher oder zusammengesetzter Datentypen erlauben. Sie werden durch Zeiger auf die jeweils folgende(n) Knoten oder Speicherzellen des Arbeitsspeichers realisiert.

Vergleich mit anderen Datenstrukturen

Im Gegensatz zu Arrays müssen die einzelnen Speicherzellen nicht nacheinander im Speicher abgelegt sein, es kann also nicht mit einfacher Adress-Arithmetik gearbeitet werden, sondern die Speicherorte müssen absolut referenziert werden. Im Gegensatz zu Bäumen sind Listen linear, d.h. ein Element hat genau einen Nachfolger. Eine Liste kann zu einem Zyklus (zyklische Liste) geschlossen werden, indem der Zeiger des letzten Listenelementes so geändert wird, dass er auf ein beliebiges Listenelement (nicht unbedingt das erste) zeigt. Dieses Listenelement (und nur dieses) hat dann zwei Vorgänger, alle anderen Elemente haben genau einen Vorgänger. Ob eine Liste zyklisch ist oder nicht, kann mit dem Hase-Igel-Algorithmus effizient festgestellt werden.

Knoten

Ein Knoten (engl. node) bezeichnet ein Element der Liste, welches die Daten und einen Zeiger auf seinen Nachfolger enthält.

Typen

Man unterscheidet grundsätzlich zwischen einfach und mehrfach oder doppelt verketteten Listen.

Einfach verkettete Liste

Sie ist die einfachste Form der verketteten Liste, da sie neben den einzelnen Knoten nur einen "Start"-Zeiger besitzt. Dieser zeigt auf den ersten Knoten in der Liste (roter Pfeil). Der letzte Knoten in der Liste zeigt auf den Nullwert (hier NIL für Not In List). (Als Nullwert (kurz NULL oder NIL) bezeichnet man in der Informatik einen Wert, der das Fehlen eines gültigen Wertes anzeigen soll. Er steht für „nicht vorhanden“ und darf nicht mit dem Zahlenwert 0 verwechselt werden. Die Vereinbarung eines undefinierten Werts ist eine wesentliche semantische bzw. pragmatische Ergänzung der Informatik (bzw. Angewandten Mathematik) gegenüber der theoretischen Mathematik.

Verbale Definition: Eine Liste ist entweder leer oder sie besteht aus einem Kopf und einem Zeiger, der wiederum eine Liste ist.

Vorteile

• Elemente können sehr schnell am Anfang der Liste eingefügt werden; sehr geringer Speicherbedarf
• Im Gegensatz zu einem Array ist das Einfügen problemlos möglich, ohne dass der komplette Datensatz bei jeder Vergrößerung umkopiert werden muss

Nachteile

• Es ist aufwändig nach Daten zu suchen, Knoten einzufügen, zu löschen und die Liste zu sortieren, da über jedes einzelne Element gegangen (iteriert) werden und das Einfügen an der ersten und der letzten Stelle gesondert behandelt werden muss.

Erweiterungen Da sich die zuvor erwähnte Variante als zu umständlich (siehe Nachteile) erwiesen hat, wird oft eine der hier nachstehenden Erweiterungen verwendet.

• Liste mit "Ende"-Zeiger: Führt einen Zeiger Ende ein, der auf das letzte Element der Liste zeigt.

Vorteile:

• Es können Elemente zusätzlich sehr schnell an das Ende der Liste angehängt werden

Nachteile:

• Etwas mehr Speicherbedarf

Doppelt (mehrfach) verkettete Liste

Verkettete Liste

Im Gegensatz zur einfach-verketteten Liste hat jedes Element sowohl einen Zeiger auf das nachfolgende als auch auf das vorhergehende Element.

Der Vorgänger-Zeiger des ersten Elementes zeigt auf ein Dummy-Element (NULL), wie auch der Nachfolger-Zeiger des letzten Elementes. Dieses besondere Element dient zum Auffinden des Anfangs und des Endes einer doppelt verketteten Liste.

Vorteile

• Die Elemente in der zweiten Hälfte einer sortierten Liste sind schneller aufzufinden.
• Schnelles Löschen und Einfügen von Elementen.
  • Das macht zum Beispiel das effiziente Sortieren der Liste möglich.
• Über die Liste kann von hinten nach vorne iteriert werden.

Nachteile

• Höherer Speicherbedarf für die zusätzlichen Zeiger.

Weitere Formen

Liste mit Listenkopf

Der Listenkopf ist ein spezieller Knoten am Anfang der Liste, der zusätzliche Informationen, wie z.B. die Anzahl der Knoten in der Liste, enthält. Der wesentlichste Vorteil ist, dass das Einfügen des 1. Elements kein Sonderfall ist.

Skip-Liste

Wie verkettete Listen werden auch bei der Skipliste die Daten in Containern abgelegt. Diese enthalten einen Schlüssel und einen Zeiger auf den nächsten Container. Allerdings können Container in Skiplisten auch Zeiger auf andere Container enthalten, welche nicht direkt nachfolgen. Es können also Schlüssel übersprungen werden. Jeder Container hat eine bestimmte Höhe h, welche um 1 kleiner ist als die Anzahl der Zeiger die ein Container enthält. Die Zeiger werden von 0 bis h nummeriert.

Bei den Skip-Listen unterscheidet man drei Arten von Typen:

1. ausgeglichene SkipList
2. unausgeglichene SkipList (siehe Bild)
3. randomisierte SkipList

Bei allen Typen ist das mehrfache Auftreten des Inhaltes erlaubt. Allerdings sind die aus- und die unausgeglichene SkipList geordnet, wohingegen die randomisierte SkipList nicht notwendigerweise geordnet sein muss. Durch das Einfügen von Zwischenstationen, welches den Aufwand der Implementierung erhöht, kann die mittlere Zugriffszeit (und damit verbunden die Komplexität) gesenkt werden. Eine Erweiterung des SkipList-Prinzip ist die Verknüpfung mit dem Prinzip der doppelt verknüpften Liste, welche die Möglichkeit eines „Rücksprunges“ ermöglicht. Bei einer ausgeglichenen SkipList senkt dies allerdings nicht die Komplexität, wohingegen bei einer unausgeglichenen SkipList auf Zwischenstationen verzichtet werden kann, welches dann wiederum den Zugriff auf Elemente in der Nähe der nächsten Zwischenstation erhöht.

Die Operationen Einfügen, Suchen und Löschen haben jeweils eine erwartete Laufzeit von $\mathcal{O}(\log n)$.

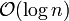Berechnung der Containerhöhe

Bei der randomisierten Skipliste erfolgt die Berechnung der Höhe h nach dem Zufallprinzip. Die Wahrscheinlichkeit, dass eine bestimmte Höhe erreicht wird kann folgendermaßen ermittelt werden: $\frac{1}{2\cdot 2^h}$

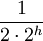
Bei nicht randomisierten Skiplisten wird die Höhe so bestimmt, dass jeder Zeiger mit Zeigerhöhe z auf einen Container 2ⁱ Positionen weiter hinten in der Liste zeigen kann. Also alle Container dazwischen eine geringere Höhe haben als der Zeiger.

Adaptive Listen

Da der Aufwand des Zugriffes auf ein Element einer einfach verknüpften Liste mit der Entfernung vom Start um n Schritte zunimmt, kam man auf das Prinzip der adaptiven Listen. Dieses Prinzip geht von der Voraussetzung des zunehmenden Zugriffsaufwandes aus und sortiert die Listenelemente nach ihrer Zugriffshäufigkeit (vergangenheitssortiert). Dabei gibt es drei grundsätzliche Strategien:

• MoveToFront: Bei jedem Zugriff auf ein Element wird dieses entfernt und am Anfang der Liste eingefügt.
• Transpose: Bei jedem Zugriff auf ein Element wird es mit seinem Vorgänger vertauscht (Sonderfall: 1. Element)
• Gratification: Zu jedem Element werden dessen Zugriffshäufigkeit gespeichert. In einem bestimmten Intervall wird anhand der Zugriffshäufigkeit die Liste neu sortiert.

Listen in der objektorientierten Programmierung

In der objektorientierten Programmierung zeichnen sich Listen gemäß dem Prinzip der Kapselung durch eine Menge von Listenoperationen aus. Intern können dabei unterschiedliche und durchaus auch kompliziertere Datenstrukturen, wie binäre Bäume zum Einsatz kommen. Aufgrund der internen Datenstruktur können dabei oft auch weitere Funktionen, wie z.B. Sortierung, sortiertes Einfügen, Entfernen des größten Elementes, etc. angeboten werden.

Je nach Einsatzzweck kann es sinnvoll sein, zwischen konkreten Implementierungen der Schnittstelle Liste zu wählen. Wird beispielsweise hauptsächlich wahlfrei über Index auf die Liste zugegriffen, wäre eine verkettete Liste eine schlechte Wahl, da dort n Operationen nötig sind, um das nte Element zu adressieren.

Daher werden in objektorientierten Bibliotheken oft neben der Schnittstelle verschiedene konkrete Implementierungen angeboten. Beispielsweise gibt es in der Programmiersprache Java als Schnittstelle java.util.List und als konkrete Implementierungen unter anderem java.util.LinkedList und java.util.ArrayList.

Listen in der Programmiersprache LISP

Listen sind neben den Einzelwerten (Atomen) die Basisdatenstruktur der Programmiersprache LISP. Programme sind Listen von Listen.

Beispiele

Nachfolgend Beispiele in Pseudocode (an C angelehnt). Dabei gibt es in der Liste das Feld Key (also den Schlüssel, den man sucht) und das Feld Data (die Nutzdaten, die hinter dem Schlüssel stecken). Das Beispiel:

• Gib mir die Lottozahlen vom 1. Januar 2006. Dabei ist 1. Januar 2006 der Schlüssel und die Lottozahlen sind die Nutzdaten.
• pNext in einem Knoten (Element) ist der Zeiger auf das nächste Element in der Liste

Neues Element in Liste einfügen

  FUNKTION insertElement( Datum, Lottozahlen ) 
  {
     Zeiger *NeuesElement = Speicherallozierung(size(Datum) + size(Lottozahlen));
  
     WENN (Speicherallozierung erfolgreich)
     {
        Kopieren von Datum und Lottozahlen nach *NeuesElement;
        NeuesElement->pNext = NULL;
        Zeiger *LetztesElement = FindeLetztesElement();
  
        WENN (Letztes Element gefunden)
        {
           LetztesElement->pNext = NeuesElement;
           return GELUNGEN;
        }
        SONST
        {
           return FEHLER;
        }
  
     }
     SONST
     {
        return FEHLER;
     }
  }

Element suchen

  FUNKTION sucheElement( Datum ) 
  {
  
     Variable lz = NULL;
     Zeiger *AktuellesElement = ErstesElement();
  
     WENN (Suche erfolgreich)
     {
        SOLANGE (lz == NULL UND AktuellesElement != NULL)
        {
           WENN (AktuellesElement->Datum == Datum)
              lz = AktuellesElement->Lottozahlen;
           SONST
              AktuellesElement = AktuellesElement->pNext;
        }
  
        WENN (lz != NULL)
           return lz;
        SONST
           return FEHLER;
     }
     SONST
     {
        return FEHLER;
     }   
  }

Element aus Liste löschen

  FUNKTION deleteElement( Datum ) 
  {   
     Zeiger *aktuellesElement = NULL;
     Zeiger *nächstesElement = ErstesElement();
  
     SOLANGE ( nächstesElement != NULL )
     {
        WENN (nächstesElement->Datum == Datum) // zu löschendes Element gefunden
        {
           WENN ( aktuellesElement != NULL ) // wir befinden uns nicht am Listenbeginn
           {
              WENN ( nächstesElement->pNext != NULL) // wir befinden uns nicht am Listenende
              {
                 aktuellesElement->pNext = nächstesElement->pNext;
                 Lösche nächstesElement;
              }
              SONST // wir befinden uns am Listenende
              {
                 aktuellesElement->pNext = NULL;
                 Lösche nächstesElement;
              }
           }
           SONST // wir befinden uns am Listenbeginn
           {
              WENN ( nächstesElement->pNext != NULL) // wir befinden uns nicht am Listenende
                 Setze Listenbeginn auf nächstesElement->pNext;               
              SONST wir befinden uns am Listenende - wir löschen das einzige Element, Liste ist nun leer
                 Setze Listenbeginn auf NULL;
  
              Lösche nächstesElement;
           }
        }
        AktuellesElement = nächstesElement;
        nächstesElement = nächstesElement->pNext,
     }
  }

Weblinks

• Einführung in verkettete Listen (englisch)
• Tutorial zu verketteten Listen (englisch)