- Deterministische Maschine
-
Ein deterministischer endlicher Automat (DEA, engl.: DFA=deterministic finite automaton) ist ein endlicher Automat, der unter Eingabe eines Zeichens seines Eingabealphabetes (mögliche Eingaben) von einem Zustand, in dem er sich befindet, in einen eindeutig bestimmten Folgezustand wechselt.
Formal kann ein DEA
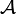 als 5-Tupel
als 5-Tupel 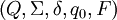 definiert werden. Hierbei gilt Folgendes:
definiert werden. Hierbei gilt Folgendes:- Q (oft auch Z oder S) ist eine Zustandsmenge, eine nichtleere endliche Menge von Zuständen. Zum Beispiel z0, z1 und z2 oder auch „Getränkeautomat wartet auf Eingabe“, „Kaffee ausschenken“, „Wechselgeld zurückgeben“, …
- Σ ist ein endliches Eingabealphabet, also erlaubte Eingaben, wie z. B. 1 und 0 oder auch „Münze einwerfen“, „Taste für Milchkaffee drücken“, „Taste Abbruch drücken“, …
- Es gibt eine Übergangsfunktion
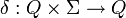 , so dass für
, so dass für 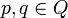 und
und 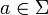 gilt δ(q,a) = p. δ ordnet jedem Paar, bestehend aus einem Zustand q und einem Eingabesymbol a, einen neuen Zustand p zu. Der Automat wechselt also von einem Zustand q in einen anderen Zustand p, wenn im Zustand q eine (gültige) Eingabe a gemacht wurde. Beispiel: δ(z0, 1) = z2 oder δ(„Getränkeautomat wartet auf Eingabe“, „Taste für Milchkaffe gedrückt“) = "Kaffee ausschenken"
gilt δ(q,a) = p. δ ordnet jedem Paar, bestehend aus einem Zustand q und einem Eingabesymbol a, einen neuen Zustand p zu. Der Automat wechselt also von einem Zustand q in einen anderen Zustand p, wenn im Zustand q eine (gültige) Eingabe a gemacht wurde. Beispiel: δ(z0, 1) = z2 oder δ(„Getränkeautomat wartet auf Eingabe“, „Taste für Milchkaffe gedrückt“) = "Kaffee ausschenken" 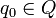 ist der Startzustand. Statt q0 wird oft auch z0 verwendet. Beispiel: z0 oder „Getränkeautomat wartet auf Eingabe“.
ist der Startzustand. Statt q0 wird oft auch z0 verwendet. Beispiel: z0 oder „Getränkeautomat wartet auf Eingabe“.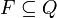 (oft auch A) ist die Menge der akzeptierenden Zustände, die sogenannten Finalzustände. Zum Beispiel: z2 oder „Getränkeautomat wartet auf Eingabe“ (in diesem Fall ist der Startzustand auch ein Finalzustand)
(oft auch A) ist die Menge der akzeptierenden Zustände, die sogenannten Finalzustände. Zum Beispiel: z2 oder „Getränkeautomat wartet auf Eingabe“ (in diesem Fall ist der Startzustand auch ein Finalzustand)
Wenn sich der Automat nach dem Lesen des Eingabewortes
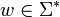 , also einer Folge von Eingaben und den damit verbundenen Zustandsübergängen, in einem Finalzustand aus F befindet, so gehört w zur Sprache
, also einer Folge von Eingaben und den damit verbundenen Zustandsübergängen, in einem Finalzustand aus F befindet, so gehört w zur Sprache 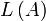 .
.Ist ein DEA in der Lage jedes Wort über dem betrachteten Alphabet bis zum Ende lesen zu können, auch wenn es nicht in der zu akzeptierenden Sprache enthalten ist, wird er vollständig genannt.
Nichtdeterministische endliche Automaten (NEAs), DEAs und Typ-3-Grammatiken (vgl. Chomsky-Hierarchie) beschreiben die gleiche Sprachklasse. NEAs lassen sich mittels Potenzmengenkonstruktion in äquivalente DEAs wandeln.
Minimierung
Zu jedem DEA existiert ein (bis auf die Benennung der Zustände) eindeutiger minimaler Automat, der dieselbe Sprache akzeptiert.
Da die Zustände des Minimalautomaten den Äquivalenzklassen der vom endlichen Automaten M akzeptierten Sprache unter der Nerode-Relation entsprechen, spricht man auch vom Äquivalenzklassenautomat:
Sei M = (Q,Σ,δ,q0,F) ein deterministischer endlicher Automat. Dann ist N = (Q',Σ,δ',q0',F') mit
der Äquivalenzklassenautomat zu M.
Die Minimierung eines deterministischen Automaten kann algorithmisch durch fortwährende Verfeinerung der Äquivalenzklassen gelöst werden. Man beginnt mit den Zustandsmengen F und Q − F. Für jeden Buchstaben aus dem Alphabet wird nun jede Zustandsmenge dahingehend aufgeteilt, dass die Überführungsfunktion die Zustände jeder neuen Menge den Buchstaben in eine jeweils eindeutige Menge abbildet. Dies wird so oft wiederholt bis sich keine Änderung mehr ergibt.
Siehe auch
Literatur
- John E. Hopcroft, Jeffrey D. Ullman: Einführung in die Automatentheorie, Formale Sprachen und Komplexitätstheorie. 2. Auflage. Pearson Studium, Reading 2002, ISBN 3-8273-7020-5
- Gottfried Vossen, Kurt-Ulrich Witt, Grundkurs Theoretische Informatik 3.Auflage, ISBN 3-528-23147-5
- Peter Sander, Wolffried Stucky, Rudolf Herschel: Automaten, Sprachen, Berechenbarkeit. Teubner, Stuttgart 1992, ISBN 3-519-02937-5
- Uwe Schöning: Ideen der Informatik, Grundlegende Modelle und Konzepte. Oldenbourg, München 2006, ISBN 3-486-57833-2
Wikimedia Foundation.

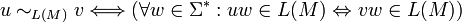
![Q' = \Big\{[w]_{L(M)} \mid w \in \Sigma^*\Big\}](/pictures/dewiki/102/ff4cae40639ec055e0e9b36275601796.png)
![~q'_0 = [\epsilon]_{L(M)}](/pictures/dewiki/55/7d572842f319c63efc440ca1a8f47039.png)
![~\delta'([u]_{L(M)} ,a)=[ua]_{L(M)}](/pictures/dewiki/99/cc30a001166667abf09e50a82c8980e1.png)
![F' = \Big\{[u]_{L(M)} \mid u \in L(M)\Big\}](/pictures/dewiki/97/aed4237d9cfc5f5f518cccd9f3a0bdbe.png)