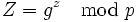Diffie-Hellman-Verfahren

Der Diffie-Hellman-Schlüsselaustausch oder Diffie-Hellman-Merkle-Schlüsselaustausch ist ein Protokoll aus dem Bereich der Kryptografie. Mit ihm erzeugen zwei Kommunikationspartner einen geheimen Schlüssel, den nur diese beiden kennen. Dieser Schlüssel wird üblicherweise verwendet, um verschlüsselte Nachrichten mittels eines symmetrischen Kryptosystems zu übertragen.

Beim Diffie-Hellman-Schlüsselaustausch senden sich beide Kommunikationspartner über einen unsicheren Kanal jeweils eine Nachricht zu. Das Problem, aus diesen beiden Nachrichten den geheimen Schlüssel zu berechnen, wird als Diffie-Hellman-Problem bezeichnet. Von diesem nimmt man an, dass es praktisch nicht lösbar ist. Deshalb kann jemand, der beide Nachrichten mithört, daraus im Allgemeinen nicht den geheimen Schlüssel berechnen. Der Diffie-Hellman-Schlüsselaustausch ist jedoch nicht mehr sicher, wenn sich ein Angreifer zwischen die beiden Kommunikationspartner schalten und Nachrichten verändern kann. Diese Lücke schließen Protokolle wie das Station-to-Station-Protokoll, indem sie zusätzlich digitale Signaturen und Message Authentication Codes verwenden.

Der langen Tradition von Streichlisten und Codebüchern setzte das Diffie-Hellman-Verfahren ein Ende. Noch während des Zweiten Weltkrieges mussten die Benutzer der ausgeklügelten Verschlüsselungsmaschinen (zum Beispiel die Enigma) Codebücher mit sich führen, um für jeden einzelnen Tag des Jahres zu wissen, welchen Schlüssel der Absender verwendet. Wurde ein solches Codebuch geraubt, war die Verschlüsselung hinfällig. Besonders beim Militär war die Zuteilung und der Transport solcher hochgeheimer Codebücher stets das größte Sorgenkind.

Der Diffie-Hellman-Schlüsselaustausch zählt zur Klasse der Schlüsselaustauschprotokolle und bildet die Grundlage des Elgamal-Kryptosystems.

Geschichte

Der Algorithmus wurde von Martin Hellman gemeinsam mit Whitfield Diffie und Ralph Merkle an der Stanford-Universität (Kalifornien) entwickelt und 1976 veröffentlicht^[1].

Wie erst 1997 bekannt wurde, hatte das britische Government Communications Headquarters (GCHQ) schon in den 1960er Jahren den Auftrag erteilt, auf Grund der hohen Kosten bei der damals üblichen Schlüsselverteilung einen anderen Weg für die Schlüsselverteilung zu finden.

Die von James Ellis, Clifford Cocks und Malcolm J. Williamson geäußerten Ideen ähnelten dem Diffie-Hellman-Verfahren. Das GCHQ hat einerseits wegen der Geheimhaltung, andererseits wegen des für die Briten aus Sicht der frühen 1970er Jahre fraglichen Nutzens nie ein Patent beantragt.

Funktionsweise

Prinzip des Diffie-Hellman-Schlüsselaustauschs

Zwei Kommunikationspartner (in der Abbildung sind dies Alice und Bob) wollen über ein unsicheres Medium, etwa eine Kabel- oder Funkleitung, verschlüsselt kommunizieren. Dazu soll ein symmetrisches Kryptosystem eingesetzt werden, für das beide jedoch zunächst einen gemeinsamen geheimen Schlüssel benötigen. Indem sie den Diffie-Hellman-Schlüsselaustausch durchführen, gelangen sie beide in den Besitz eines solchen Schlüssels.

1. Die Kommunikationspartner einigen sich zunächst auf eine Primzahl p und eine Primitivwurzel g modulo p mit 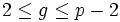$2 \le g \le p-2$. Diese Parameter müssen nicht geheim bleiben, können also insbesondere auch über ein unsicheres Medium übertragen werden.
2. Beide Kommunikationspartner erzeugen jeweils eine geheim zu haltende Zufallszahl a bzw. b aus der Menge 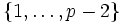$\{ 1, \ldots, p-2 \}$. a und b werden nicht übertragen, bleiben also dem jeweiligen Kommunikationspartner, aber auch potenziellen Lauschern, unbekannt.
3. Die Kommunikationspartner berechnen A = g^amod p bzw. B = g^bmod p. Nun werden A und B über das unsichere Medium übertragen.
4. Die Kommunikationspartner berechnen nun K = B^amod p bzw. K = A^bmod p. Das Ergebnis K ist für beide Partner gleich und kann als Schlüssel für die weitere Kommunikation verwendet werden.

Dass beide Kommunikationspartner denselben Wert für K berechnen, zeigen die folgenden beiden Gleichungen:

K = B^amod p = (g^bmod p)^amod p = g^bamod p = g^abmod p

K = A^bmod p = (g^amod p)^bmod p = g^abmod p

Beispiel

Die Kommunikationspartner seien Alice und Bob. Das Beispiel benutzt sehr kleine Zahlen. In der tatsächlichen Anwendung werden Zahlen mit mehreren hundert Dezimalstellen benutzt.

1. Alice und Bob einigen sich auf p = 13 und g = 2.
2. Alice wählt die Zufallszahl a = 5. Bob wählt die Zufallszahl b = 7.
3. Alice berechnet A = 2⁵mod 13 = 6 und sendet dieses Ergebnis an Bob.
4. Bob berechnet B = 2⁷mod 13 = 11 und sendet dieses Ergebnis an Alice.
5. Alice berechnet K = 11⁵mod 13 = 7.
6. Bob berechnet K = 6⁷mod 13 = 7.
7. Beide erhalten das gleiche Ergebnis K = 7.

Ein eventuell vorhandener Lauscher könnte zwar die Zahlen 13, 2, 6 und 11 mithören, das eigentliche gemeinsame Geheimnis von Alice und Bob K = 7 bleibt ihm aber verborgen.

Sicherheit

Diffie-Hellman-Problem

Als Diffie-Hellman-Problem bezeichnet man die folgende Aufgabenstellung :

Wenn ein Element g einer Gruppe und die Werte g^a und g^b gegeben sind, welchen Wert hat dann g^ab?

Da dieses Problem in bestimmten Gruppen nur mit enormen Rechenaufwand zu lösen ist, kann ein Angreifer aus den beiden beim Diffie-Hellman-Schlüsselaustausch übertragenen Nachrichten nicht den erzeugten Schlüssel berechnen.

Das Diffie-Hellman-Problem ist eng verwandt mit dem Diskreter-Logarithmus-Problem. Ueli Maurer konnte zeigen, dass man das Diffie-Hellman-Problem lösen kann, wenn man diskrete Logarithmen berechnen kann. Er hat auch gezeigt, dass beide Probleme unter bestimmten Voraussetzungen äquivalent sind.^[2] Es ist keine Möglichkeit bekannt, das Diffie-Hellman-Problem zu lösen, ohne diskrete Logarithmen zu berechnen.

Man-in-the-Middle-Angriff ^[3]

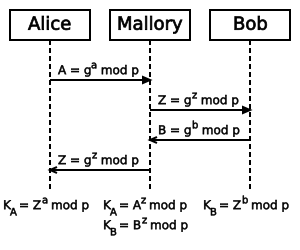
Der Diffie-Hellman-Schlüsselaustausch ist nicht mehr sicher, wenn der Angreifer bei einem Man-In-The-Middle-Angriff Datenpakete verändern kann. Der Angreifer fängt dann die von Alice und Bob gesendeten Nachrichten ab und sendet statt dessen jeweils eine eigene Nachricht

$Z = g^z \mod p$

weiter, die er aus einer beliebigen Zahl z und den öffentlich bekannten Zahlen g und p berechnet.

Am Schluss des Schlüsselaustauschs besitzen die beiden Kommunikationspartner Alice und Bob unterschiedliche Schlüssel K_A und K_B. Im Prinzip wurde zweimal ein Diffie-Hellman-Schlüsselaustausch durchgeführt: ein Mal zwischen Alice und der Angreiferin Mallory und ein Mal zwischen Mallory und Bob. Dabei erlangt Mallory Kenntnis der beiden Schlüssel K_A und K_B.

K_A = Z^amod p = (g^z)^amod p = (g^a)^zmod p = A^zmod p

K_B = Z^bmod p = (g^z)^bmod p = (g^b)^zmod p = B^zmod p

Da Alice und Bob im Weiteren davon ausgehen mit dem jeweils Anderen zu kommunizieren, kann Mallory die folgende symmetrisch verschlüsselte Kommunikation abhören. Diese leitet sie dazu weiterhin über sich selbst um. Daten von Alice entschlüsselt Mallory mit K_A und verschlüsselt sie wieder mit K_B bevor sie sie an Bob weiterschickt. Dabei kann Mallory den Nachrichteninhalt sowohl lesen, als auch unbemerkt verändern. Die gleiche Vorgehensweise wendet sie auch für die Gegenrichtung an.

Um einen solchen Man-In-The-Middle-Angriff auszuschließen, müssen die ausgetauschten Nachrichten authentifiziert werden. Dazu verwendet man digitale Signaturen und Message Authentication Codes.

Andere Gruppen

Für den Diffie-Hellman-Schlüsselaustausch können neben den ganzen Zahlen auch andere Gruppen verwendet werden. Es sind alle Gruppen geeignet, in denen man Potenzen effizient berechnen kann und das Diffie-Hellman-Problem schwer zu lösen ist. Beispiele für solche Gruppen sind alle primen Restklassengruppen 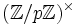$(\mathbb{Z} / p \mathbb{Z} )^\times$ modulo einer Primzahl.^[4]

Literatur

• Johannes Buchmann: Einführung in die Kryptographie. 2. Auflage. Springer-Verlag, 2003, ISBN 3-540-41283-2, S. 129−133
• Simon Singh: Geheime Botschaften, dtv 2001, ISBN 3-423-33071-6

Weblinks

• Beispiel für den Diffie-Hellman-Algorithmus
• RFC 2631 – E. Rescorla: Diffie-Hellman Key Agreement Method, Juni 1999. (englisch)
• Empfohlene Paramater für p und g beim Diffie-Hellman-Austausch
• Diffie-Hellman explained visually
• Publikationsliste zu Themenkomplex „Diskreter-Logarithmus-Problem und Diffie-Hellman-Problem“ (Autor: Ueli Maurer)

Einzelnachweise

1. ↑ Diffie, W. and Hellman, M. E. (1976) New Directions in Cryptography, IEEE Transactions on Information Theory (22:6), pp. 644-654.
2. ↑ Ueli Maurer: Towards the equivalence of breaking the Diffie-Hellman protocol and computing discrete logarithms. In: Advances in Cryptology - Crypto '94. Springer-Verlag, 1994, S. 271−281.
3. ↑ Shafi Goldwasser, Mihir Bellare: Lecture Notes on Cryptography. 2001, S. 202
4. ↑ Alfred J. Menezes, Paul C. van Oorschot, Scott A. Vanstone: Handbook of Applied Cryptography. CRC Press, 1996, ISBN 0-8493-8523-7, S. 515–517