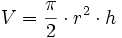Drehparaboloid

Rotationsparaboloid

Ein Rotationsparaboloid ist in der Mathematik der Rotationskörper einer Parabel, also die dreidimensionale Figur, die entsteht, wenn man eine (zweidimensionale) Parabel um ihre Symmetrieachse rotieren lässt.

Beispiele aus dem täglichen Leben sind Reflektoren von Scheinwerfern oder Parabolspiegel der Weltraumforschung.

Wenn man eine Flüssigkeit gleichmäßig um eine senkrechte Achse dreht, dann überlagern sich Schwerkraft und Fliehkraft, und die Flüssigkeitsoberfläche nimmt die Form eines Rotationsparaboloids an. So funktioniert das Quecksilber-Teleskop, und so kann man auch Teleskop-Spiegel gießen, um danach nicht so viel Material abschleifen zu müssen, da die beim Guss erhaltene Oberfläche bereits ein Rotationsparaboloid darstellt.

Zur Verwendung von Rotationsparaboloiden als Spiegel siehe im Artikel über die sog. Parabolspiegel.

Das Rotationsparaboloid ist ein Sonderfall des Paraboloids.

Formeln

Die Formeln gelten für ein Rotationsparaboloid, das von einer zur z-Achse senkrechten Ebene (xy-Ebene) in der Höhe h abgeschnitten wird. Der Schnittkreis besitzt den Radius r.

Volumen 

$V = \frac{\pi}{2} \cdot r^2 \cdot h$

Weblinks

Quecksilber-Spiegelteleskop: [1]