Parabel (Mathematik)

Die Parabel ist einer der Kegelschnitte

Ein hüpfender Ball beschreibt – wenn man den Reibungsverlust vernachlässigt – Parabelbögen.

Wasserstrahlen können ebenfalls Parabeln beschreiben.

In der Mathematik ist eine Parabel (von lat. parabola zu altgriechisch παραβολή parabolē ‚Nebeneinanderstellung, Vergleichung, Gleichnis‘; zurückzuführen auf παρά pará ‚neben‘ und βάλλειν bállein ‚werfen‘)^[1] eine Kurve zweiter Ordnung. Neben dem Punkt, dem Kreis, der Ellipse und der Hyperbel zählt sie zu den Kegelschnitten, bei denen sie die Exzentrizität eins hat. Sie ist wie der Kreis eine spezielle Ellipse. Bei ihr liegt einer der beiden Ellipsen-Brennpunkte im Unendlichen, beim Kreis fallen beide zusammen.

Ein Körper, der sich in einem homogenen Gravitationsfeld ohne Einwirkung anderer Kräfte bewegt, folgt einer parabelförmigen Bahn. In radialsymmetrischen Gravitationsfeldern, wie sie um einen Himmelskörper herrschen, ist die Parabel eine der möglichen Keplerbahnen.

In kartesischen Koordinaten hat eine nach oben (y-Richtung) geöffnete Parabel mit Scheitel im Ursprung die Gleichung

y = ax² mit a > 0 .

Allgemein wird eine nach oben oder unten geöffnete Parabel durch die Gleichung

y = ax² + bx + c mit $a,b,c \in \R$, $a \ne 0$

beschrieben. Sie ist also der Graph einer quadratischen Funktion

f(x) = ax² + bx + c.

Allgemeiner werden in der Analysis unter Parabeln auch die Funktionsgraphen von beliebigen ganzrationalen Funktionen verstanden. Hat die Funktion den Grad n, dann wird der Graph als Parabel der Ordnung n bezeichnet.

In der Geometrie werden jedoch nur die Funktionsgraphen von quadratischen Funktionen als Parabeln bezeichnet.

Die Parabel wurde von Menaichmos entdeckt und von Apollonios von Perge benannt, die Bezeichnung bezieht sich auf die Exzentrizität ε, welche für die Parabel gleich 1 ist.^[2]

Definition mit Leitgerade

Eine Parabel mit Leitgerade

Außer als Kegelschnitt kann eine Parabel geometrisch auch als Ortslinie beschrieben werden:

Eine Parabel ist der geometrische Ort aller Punkte X, deren Abstand zu einem speziellen festen Punkt – dem Brennpunkt F – gleich dem zu einer speziellen Geraden – der Leitgeraden l – ist.

Als Punktmenge notiert:

$\{X \mid\overline{XF} = \overline{Xl}\}$

Der Punkt, der in der Mitte zwischen Brennpunkt und Leitgerade liegt, heißt Scheitel A der Parabel. Die Verbindungsgerade von Brennpunkt und Scheitel wird auch Achse der Parabel genannt. Sie ist die einzige Symmetrieachse der Parabel.

Eigenschaften

Koeffizienten

Da die Parabel nur von einem Parameter abhängig ist (dem Abstand 2f von Leitgerade und Brennpunkt bzw. dem Parameter a in der obigen Gleichung), sind alle Parabeln zueinander ähnlich. Die Unterschiede in der Krümmung entstehen nur durch das Vergrößerungsverhältnis. Insbesondere ist die numerische Exzentrizität $\epsilon = 1$ und die lineare Exzentrizität gleich der Brennweite

$e = f = \tfrac 1{4a}$ .

Für a = 1, d. h.: $f = \tfrac 14$, spricht man auch von einer Grundparabel oder Normalparabel mit der Koordinatengleichung y = x².

Die Parabel ist wie der Kreis eine spezielle Ellipse. Bei ihr liegt einer der beiden Ellipsen-Brennpunkte im Unendlichen, beim Kreis fallen beide zusammen.

Sie kann auch als Grenzfall einer Hyperbel angesehen werden, bei der ein Brennpunkt fix ist und der andere unendlich weit in die eine oder andere Richtung verschoben ist.

Brennpunkt

Parabel (blau) mit zum Brennpunkt F reflektierten Strahlen (rot)

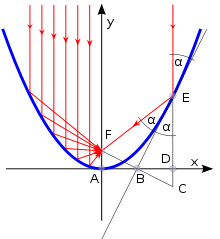
Wird ein Strahl, der parallel zur Achse einfällt, an der Parabel beziehungsweise an ihrer Tangente gespiegelt, so geht der resultierende Strahl durch den Brennpunkt, und umgekehrt. Dieser resultierende Strahl wird auch Brennlinie, Leitstrahl, oder Brennstrahl des Punktes genannt. Diese Eigenschaft hat auch ein Rotationsparaboloid, also die Fläche, die entsteht, wenn man eine Parabel um ihre Achse dreht; sie wird häufig in der Technik verwendet (siehe Parabolspiegel).

Die Lage des Brennpunkts lässt sich aus Dreiecksbeziehungen ablesen: Gesucht ist die Länge der Strecke | AF | einer Parabel, die durch die Formel $y = a \cdot x^2$ gegeben ist. Ein Lichtstrahl, der an der Parabel reflektiert wird, verlässt die Oberfläche der Parabel unter dem gleichen Winkel α, unter dem er eintrifft. Dieser Winkel findet sich als Gegenwinkel in dem an der Kante BE gespiegelten Dreieck BCE wieder. Die beiden Dreiecke BFE und BCE haben die gleiche Form und Größe und sind kongruent. Damit sind auch die beiden Dreiecke AFB und BDC kongruent. Nun lässt sich der Höhensatz auf das Dreieck BCE anwenden:

$|BD|^2 = |CD| \cdot |DE| = |AF|\cdot|DE|$

Das zweite Gleichungszeichen gilt, weil AFB und BDC kongruent sind. Andererseits hängt die Strecke | DE | über die Parabelgleichung mit der Strecke | AD | zusammen:

$|DE| = a\cdot |AD|^2$

Der Punkt B teilt die Strecke AD genau in der Mitte. Also gilt | AD | = 2 | BD | . Einsetzen in die Gleichung für | DE | und dann in die Gleichung für | BD | ² und Auflösen nach | AF | ergibt:

$|AF| = \frac 1{4a}$

Der Abstand zwischen dem Scheitelpunkt und dem Brennpunkt einer Parabel, die durch die Gleichung $y = a \cdot x^2$ gegeben ist, beträgt also $\tfrac 1{4a}$.

Umgekehrt kann man bei bekannter Brennweite f = | AF | aus den obigen Beziehungen die Gleichung der Parabel herleiten. Setzt man x = | AD | = 2 | BD | und y = | DE | , so ergibt sich:

$y = |DE| = \frac{|BD|^2}{|AF|} = \frac 1{4 \,f} \,x^2$

Lagebeziehungen

Eine Parabel heißt in Hauptlage, wenn ihr Scheitelpunkt im Koordinatenursprung liegt und ihre Achse mit einer Koordinatenachse zusammenfällt. In der 1. Hauptlage ist die Parabel nach rechts offen; die Achse der Parabel fällt mit der positiven x-Achse zusammen. In 2. Hauptlage befindet sich die Parabel, wenn sie nach oben offen ist bzw. ihre Achse mit der positiven y-Achse zusammenfällt. Analog dazu sind 3. Hauptlage (nach links offen) und 4. Hauptlage (nach unten offen) definiert.

In 2. und 4. Hauptlage kann eine Parabel als mathematische Funktion mit der Funktionsgleichung y = ax² aufgefasst werden (a > 0 für die 2. Hauptlage, a < 0 für die 4. Hauptlage). In 1. und 3. Hauptlage wird die Parabel durch eine Gleichung der Form y² = ax beschrieben (a > 0 für 1. Hauptlage, a < 0 für 3. Hauptlage). Dies ist keine Funktionsgleichung, da nicht jedem x-Wert nur ein Funktionswert entspricht. Um die Parabel in 1. bzw. 3. Hauptlage als Funktion aufzufassen, muss sie jeweils in den über bzw. unter der x-Achse liegenden Ast getrennt werden. Die zu den Ästen gehörigen Funktionen sind dann $y = \sqrt{ax}$ bzw. $y = -\sqrt{ax}$, wobei diese nur für nicht-negative x-Werte (1. Hauptlage, a > 0) bzw. nicht-positive x-Werte (3. Hauptlage, a < 0) definiert sind.

Scheitelform

Die Scheitelpunktform (auch Scheitelform) ist eine spezielle Darstellung der quadratischen Funktionen. Mit ihr kann man den tiefsten bzw. höchsten Punkt einer Parabel aus der Funktionsgleichung ablesen.

Die quadratische Funktion lautet in der Scheitelpunktform

f(x) = a(x − d)² + e.

Dabei sind d,e und $a\ne 0$ beliebige reelle Zahlen.

Der Scheitelpunkt hat dann die Koordinaten S(d | e).

Mit Hilfe der quadratischen Ergänzung kann jede quadratische Funktion auf einfache Weise in diese Form überführt werden.

Das Extremum

Anhand der Scheitelpunktform kann man direkt die Lage des Scheitelpunktes, also des einzigen Extrempunkts S(d | e) erkennen. Es gilt dann f(d) = e, d gibt damit also den Extremwert an. Beispiel: f(x) = 4(x − 6)² + 8; Scheitelpunkt S(6 | 8)

Stauchung und Streckung

Durch den Koeffizienten a wird die Stauchung bzw. Streckung der Parabel und die Art der Extremstelle ausgedrückt. Die Normalparabel wird durch den Faktor $a\in\R$ gestreckt. Daraus ergeben sich die folgenden Möglichkeiten:

a > 1

Streckung bzgl. y-Achse, Parabel ist enger als die Normalparabel

a = 1

Normalparabel

0 < a < 1

Stauchung bzgl. y-Achse, Parabel ist weiter als die Normalparabel

a = 0

Die Funktion ist keine Parabel sondern eine Konstante (bzw. unendlich stark gestaucht)

− 1 < a < 0

Stauchung bzgl. y-Achse, Parabel ist weiter als die Normalparabel, Spiegelung bzgl. x-Achse

a = − 1

Spiegelung der Normalparabel bzgl. x-Achse

a < − 1

Streckung bzgl. y-Achse, Parabel ist enger als die Normalparabel, Spiegelung bzgl. x-Achse

Beispiele

• $f(x) = 2x^2 + 2 = 2(x - 0)^2 + 2; \quad a = 2, d = 0, e=2 \quad \Rightarrow \quad S(0|2)$
• $f(x) = x^2 + 4x + 4 = 1(x - (-2))^2 + 0; \quad a = 1, d = -2, e=0 \quad \Rightarrow \quad S(-2|0)$

Sonstiges

Graphische Multiplikation von 2 und 3 mithilfe einer Normalparabel

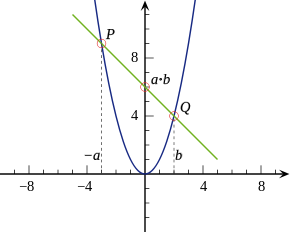
Eine Normalparabel ist eine „Multiplikationsmaschine“: Man kann mit ihr auf graphischem Wege das Produkt zweier Zahlen berechnen. Dazu zeichnet man zunächst die Normalparabel y = x² in ein kartesisches Koordinatensystem ein. Die zu multiplizierenden Faktoren trägt man auf der x-Achse ab und bestimmt für jeden Wert einen Punkt auf der Parabel. Sind die Zahlen mit a und b bezeichnet, ergeben sich also zwei Punkte P(a | a²) und Q(b | b²). Die Gerade durch P und Q schneidet die y-Achse in einem Punkt, dessen y-Koordinate den Wert − a·b hat. Im Grenzfall a = b ergibt sich die Gerade als Tangente an die Parabel.

Katenoide (rot) im Vergleich mit einer Parabel

Falls a und b gleiches Vorzeichen haben, ist es praktikabler, einen der Faktoren in negativer Richtung aufzutragen anstatt später das Vorzeichen des Ergebnisses umzudrehen, so geschehen im Beispiel mit den Werten a = 3 und b = 2. Hier trägt man die Faktoren als x-Werte mit unterschiedlichen Vorzeichen in das Koordinatensystem ein, nämlich als P( − 3 | 9) und Q(2 | 4). Verbindet man die Punkte durch eine Gerade, so erkennt man, dass der Schnittpunkt der Geraden mit der y-Achse gleich 6=2·3 ist.

Beziehung zu Katenoiden

Kettenkurven ähneln Parabeln, sind aber keine. Das Seil einer Hängebrücke, das durch sein Eigengewicht durchhängt, beschreibt eine Kettenkurve. Diese wird nicht durch eine quadratische Funktion, sondern durch den Kosinus Hyperbolicus beschrieben.

Weblinks

 Commons: Parabeln – Sammlung von Bildern, Videos und Audiodateien

 Wiktionary: Parabel – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Animierte Parabel (Java-Applet erzeugt mit GeoGebra), home.telebel.de

Einzelnachweise

1. ↑ Wilhelm Gemoll: Griechisch-Deutsches Schul- und Handwörterbuch. G. Freytag Verlag/Hölder-Pichler-Tempsky, München/Wien 1965.
2. ↑ I. N. Bronstein, K. A. Semendjajew (Begründer), Günter Grosche (Bearb.), Eberhard Zeidler (Hrsg.): Teubner-Taschenbuch der Mathematik. Teubner, Stuttgart 1996, ISBN 3-8154-2001-6, S. 24.