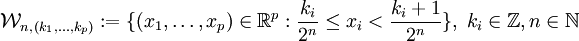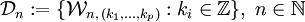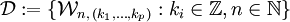Dyadisches Gitter

Die Menge der dyadischen Elementarzellen ist eine Partitionierung des p-dimensionalen Raumes und ist folgendermaßen definiert: Mit

$\mathcal{W}_{n,\,(k_1,\ldots,k_p)} := \{(x_1,\ldots,x_p) \in \R^p: \frac{k_i}{2^n} \leq x_i < \frac{k_i+1}{2^n} \},\; k_i \in \mathbb{Z}, n \in \mathbb{N}$

definiert man einen halboffenen Würfel im 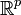$\R^p$, der die Kantenlänge 2 ^{− n} hat.

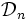$\mathcal{D}_n$ bezeichnet die Menge der dyadischen Elementarzellen der Ordnung n:

$\mathcal{D}_n := \{\mathcal{W}_{n,\,(k_1,\ldots,k_p)}: k_i \in \mathbb{Z} \}, \; n \in \mathbb{N}$

Die Menge aller dyadischen Elementarzellen im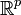 $\R^p$ wird dann mit 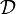$\mathcal{D}$ bezeichnet:

$\mathcal{D} := \{ \mathcal{W}_{n,\,(k_1,\ldots,k_p)}: k_i \in \mathbb{Z} , n \in \mathbb{N}\}$

Die Menge der Eckpunkte der dyadischen Elementarzellen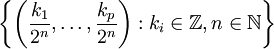 $\left\{\left(\frac{k_1}{2^n},\ldots,\frac{k_p}{2^n}\right): k_i \in \mathbb{Z}, n \in \mathbb{N}\right\}$ wird das dyadische Gitter genannt.

Elementarzellen selber Ordnung sind also disjunkt und voneinander durch ein Gitter getrennt.

Beispiele

• p=2: Elementarzellen sind Quadrate.
• p=3: Elementarzellen sind Würfel.