E-Reihe

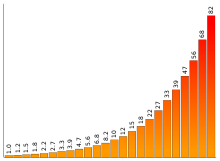
Eine E-Reihe ist eine nach der sog. Renard-Serie genormte Folge von Eigenschaftswerten elektrischer Bauelemente. Die im Handel erhältlichen Werte von Widerständen, Kondensatoren und Spulen haben bis auf seltene Ausnahmen nominelle Werte aus einer E-Reihe. Eine E-Reihe deckt dabei den Wertebereich so ab, dass das Verhältnis aufeinanderfolgender Werte möglichst gleich groß ist. Außerdem sind die Werte so gewählt, dass sich die Ziffernfolgen in jeder Dekade wiederholen.

Es gibt sieben E-Reihen: E3, E6, E12, E24, E48, E96 und E192. Die Zahl hinter dem E gibt an, wie viele Werte die Reihe innerhalb einer Dekade enthält. Die Reihen sind in der Norm DIN IEC 60063 vom Dezember 1985 Vorzugsreihen für die Nennwerte von Widerständen und Kondensatoren festgelegt. Diese ist identisch mit der internationalen Norm IEC 60063 von 1963.

Berechnung

Die Reihe E12 über zwei Dekaden

Die Nummer einer E-Reihe beschreibt die Anzahl der Nennwerte innerhalb einer Dekade. Die erste Reihe ist E3 mit drei Werten pro Dekade. Die jeweils nächstgrößere Reihe besitzt doppelt so viele Nennwerte pro Dekade. Weitere Reihen sind E6, E12, E24, E48, E96 und E192. In den E-Reihen verteilen sich die Werte innerhalb einer Dekade nicht linear, sondern logarithmisch. Die Werte innerhalb einer Reihe werden, nach demselben Prinzip wie bei Renard-Serien, durch folgende mathematische Folge beschrieben:

$k = \sqrt [n]{10^m}$, $m \in [0;n] \cap \mathbb{Z}$, n = E-Reihe.

Die Glieder der Folge werden so gerundet, dass sich bei den Reihen E3 bis E24 zwei und bei den Reihen E48 bis E192 drei signifikante Stellen und außerdem zwischen benachbarten Folgengliedern minimale Differenzen ergeben. Die jeweils nächst präzisere Widerstandsreihe ergibt sich durch Verdoppelung der Zahl und Halbierung der Toleranz. Die höhere E-Reihe enthält jeweils alle Werte der untergeordneten Reihen.

Da die Reihen E3, E6, E12 und E24 schon 1948 und 1950 und damit vor der Entstehung der Norm DIN IEC 63 festgelegt wurden, entsprechen in der E24-Reihe die Werte von 2,7 bis 4,7 nicht den Rundungsregeln, was aber auf Grund der großen Verbreitung nicht mehr geändert worden ist.

Beispiel

Die Widerstandsreihe E3 hat drei Widerstandswerte pro Dekade. Deshalb gilt: n = 3.

Somit ergeben sich für die Dekade ab $m \in \lbrace 0,1,2 \rbrace$:

Der erste Widerstandswert	$m = 0: R = \sqrt [3]{10^0} = 1{,}0$
Der zweite Widerstandwert	$m = 1: R = \sqrt [3]{10^1} = 2{,}2$
Der dritte Widerstandwert	$m = 2: R = \sqrt [3]{10^2} = 4{,}7$

Da die E3-Reihe aus nur drei Werten innerhalb einer Dekade besteht, ist die Berechnung damit zu Ende; die nächsten Zahlenwerte sind 10, 22, 47, usw..

Werte

Folgend sind die festgeschriebenen Werte der Dekade ab m = 0 aufgeführt:

E3 E6 E12 E24 E48 E96 E192 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,01 1,02 1,02 1,04 1,05 1,05 1,05 1,06 1,07 1,07 1,09 1,10 1,10 1,10 1,10 1,11 1,13 1,13 1,14 1,15 1,15 1,15 1,17 1,18 1,18 1,20 1,20 1,20 1,21 1,21 1,21 1,23 1,24 1,24 1,26 1,27 1,27 1,27 1,29 1,30 1,30 1,32 1,30 1,33 1,33 1,33 1,35 1,37 1,37 1,38 1,40 1,40 1,40 1,42 1,43 1,43 1,45 1,50 1,50 1,50 1,47 1,47 1,47 1,49 1,50 1,50 1,52 1,54 1,54 1,54 1,56 1,58 1,58 1,60 1,60 1,62 1,62 1,62 1,64 1,65 1,65 1,67 1,69 1,69 1,69 1,72 1,74 1,74 1,76 1,80 1,80 1,78 1,78 1,78 1,80 1,82 1,82 1,84 1,87 1,87 1,87 1,89 1,91 1,91 1,93 2,00 1,96 1,96 1,96 1,98 2,00 2,00 2,03 2,05 2,05 2,05 2,08 2,10 2,10 2,13

E3 E6 E12 E24 E48 E96 E192 2,20 2,20 2,20 2,20 2,15 2,15 2,15 2,18 2,21 2,21 2,23 2,26 2,26 2,26 2,29 2,32 2,32 2,34 2,40 2,37 2,37 2,37 2,40 2,43 2,43 2,46 2,49 2,49 2,49 2,52 2,55 2,55 2,58 2,70 2,70 2,61 2,61 2,61 2,64 2,67 2,67 2,71 2,74 2,74 2,74 2,77 2,80 2,80 2,84 3,00 2,87 2,87 2,87 2,91 2,94 2,94 2,98 3,01 3,01 3,01 3,05 3,09 3,09 3,12 3,30 3,30 3,30 3,16 3,16 3,16 3,20 3,24 3,24 3,28 3,32 3,32 3,32 3,36 3,40 3,40 3,44 3,60 3,48 3,48 3,48 3,52 3,57 3,57 3,61 3,65 3,65 3,65 3,70 3,74 3,74 3,79 3,90 3,90 3,83 3,83 3,83 3,88 3,92 3,92 3,97 4,02 4,02 4,02 4,07 4,12 4,12 4,17 4,30 4,22 4,22 4,22 4,27 4,32 4,32 4,37 4,42 4,42 4,42 4,48 4,53 4,53 4,59

E3 E6 E12 E24 E48 E96 E192 4,70 4,70 4,70 4,70 4,64 4,64 4,64 4,70 4,75 4,75 4,81 4,87 4,87 4,87 4,93 4,99 4,99 5,05 5,10 5,11 5,11 5,11 5,17 5,23 5,23 5,30 5,36 5,36 5,36 5,42 5,49 5,49 5,56 5,60 5,60 5,62 5,62 5,62 5,69 5,76 5,76 5,83 5,90 5,90 5,90 5,97 6,04 6,04 6,12 6,20 6,19 6,19 6,19 6,26 6,34 6,34 6,42 6,49 6,49 6,49 6,57 6,65 6,65 6,73 6,80 6,80 6,80 6,81 6,81 6,81 6,90 6,98 6,98 7,06 7,15 7,15 7,15 7,23 7,32 7,32 7,41 7,50 7,50 7,50 7,50 7,59 7,68 7,68 7,77 7,87 7,87 7,87 7,96 8,06 8,06 8,16 8,20 8,20 8,25 8,25 8,25 8,35 8,45 8,45 8,56 8,66 8,66 8,66 8,76 8,87 8,87 8,98 9,10 9,09 9,09 9,09 9,20 9,31 9,31 9,42 9,53 9,53 9,53 9,65 9,76 9,76 9,88

Toleranzen

Je größer die E-Reihe, desto kleiner sind die Toleranzen der Bauteile:

E3 = über 20 %, E6 = 20 %, E12 = 10%, E24 = 5 %, E48 = 2 %, E96= 1 %, E192 = 0,5 %

In der Norm sind jedoch nur die Toleranzen für die Reihen E3 bis E24 und die maximal zulässigen Abweichungen angegeben. Für die Herstellung insbesondere von nicht abgeglichenen Widerständen ergibt sich aus den einander berührenden Toleranzbereichen, dass beliebige Werte produzierter Widerstände einem Wert zugeordnet und verkauft werden können.

Tatsächlich sind die Werte der entsprechenden Reihen jedoch auch enger toleriert erhältlich. Gut erhältlich ist z. B. bei Widerständen die Reihe E12 mit 1 % Toleranz und die Reihe E96 mit 0,1 %.

Widerstandsreihen

Widerstände E12 mit Farbcode
Angaben in  Ω:
Ziffern beginnen auf der Kappe, letzte Farbe schwarz ist der Multiplikator 10⁰=1

Einige Widerstandswerte im Überblick:

Reihe E6	10 Ω, 15 Ω, 22 Ω, 33 Ω, 47 Ω, 68 Ω (und entsprechende Werte · 10m)
Reihe E12	10 Ω, 12 Ω, 15 Ω, 18 Ω, 22 Ω, 27 Ω, 33 Ω, 39 Ω, 47 Ω, 56 Ω, 68 Ω, 82 Ω
	(und entsprechende Werte · 10m)

Siehe auch

• Liste elektronischer Bauteile
• Renard-Serie