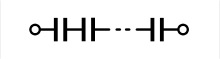Kondensator (Elektrotechnik)

Prinzipdarstellung eines Kondensators mit Dielektrikum

Ein Kondensator (von lateinisch condensare ‚verdichten‘) ist ein passives elektrisches Bauelement mit der Fähigkeit, elektrische Ladung und damit zusammenhängend Energie zu speichern. Die Fähigkeit, Ladung zu speichern, wird als elektrische Kapazität bezeichnet und in der Einheit Farad gemessen. Kondensatoren wirken Spannungsänderungen aufgrund ihrer Ladungsspeicherfähigkeit entgegen, während eine Spule Stromänderungen entgegenwirkt.

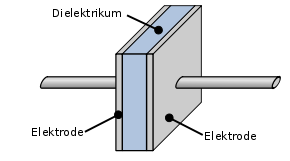
Die technische Ausführung von Kondensatoren besteht aus zwei elektrisch leitenden Flächen in meist geringem Abstand, den Elektroden, auch Kondensatorbeläge genannt. Dazwischen befindet sich immer ein Bereich mit isolierender Eigenschaft, ein Dielektrikum. Bei den meisten Bauformen werden die Elektroden und das Dielektrikum aufgerollt oder als Stapel angeordnet.

Kondensatoren werden in vielen elektrischen Anlagen und in nahezu jedem elektronischen Gerät eingesetzt. Sie realisieren beispielsweise elektrische Energiespeicher, Blindwiderstände oder frequenzabhängige Widerstände; spezielle Bauformen werden als Sensor verwendet. Bei besonderen Konfigurationen sind nichtlineare Kondensatoren bekannt.^[1] Als Kapazitätsnormal wird ein elektrischer Kondensator mit höchsten Anforderungen an die absolute und relative Kapazitätskonstanz in Bezug auf thermische Umweltänderungen und Alterung bezeichnet. Zusätzlich werden meist noch höchste Anforderungen an die elektrische Güte über einen großen Einsatzfrequenzbereich sowie Polarisationsspannungen des verwendeten Dielektrikums von weniger als einigen Mikrovolt gefordert. Auch Thermospannungen sind hier unerwünscht. Diese Eich-Kapazitätsnormale werden zur Normierung bzw. zum Abgleich hochwertiger Messgeräte, wie z. B. Präzisions-RLC-Messbrücken eingesetzt bzw. befinden sich in diesen Geräten.

Begrifflich abgegrenzt werden Anordnungen, bei denen die kapazitive Kopplung zweier Elektroden nicht das unmittelbare Ziel oder unerwünscht ist. Begriffe dieser sogenannten parasitären oder begleitenden Kapazitäten sind zum Beispiel „Streukapazität“, „kapazitive Störeinkopplung“ oder „Leitungskapazität“. Ebenfalls nicht zu den Kondensatoren wird eine Reihe von Aktoren gezählt wie piezoelektrische Wandler, elektrostatische Lautsprecher, Ablenkplatten und Bauelemente der Elektrooptik. Diese haben zwar einen ähnlichen Aufbau, der jedoch unmittelbar nur der Erzeugung eines elektrischen Feldes dient. Teilweise weisen diese Aktoren relativ hohe, meist hier aber unerwünschte Eigenkapazitäten im Nano-Farad-Bereich auf.

Funktionsweise

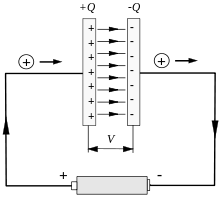
Ein elektrischer Stromfluss durch einen Kondensator hindurch lädt eine der Elektroden positiv, die andere negativ auf. Allgemein ausgedrückt wird die auf den Elektroden gebildete Ladung vom Kondensator gespeichert.

Prinzipielle Darstellung des Stromflusses durch einen Kondensator mit der Bildung eines elektrischen Feldes und der Aufladung der Elektroden, wobei eine Spannung V entsteht

Zwischen den beiden Elektroden des Kondensators fließt der Strom als Verschiebungsstrom, der mit einer entsprechenden Änderung der elektrischen Feldstärke einhergeht. Ein weiterer Stromfluss gegen die sich aufbauende Spannung erhöht die innere Energie des Kondensators. Wird der Kondensator von der Stromquelle getrennt, so bleiben Energie und Ladungen erhalten, die Spannung bleibt konstant. Wird durch Umkehr der Stromrichtung Energie entnommen, sinkt die Spannung wieder.

Ist der Raum zwischen den Elektroden mit einem Dielektrikum ausgefüllt, so besteht der Verschiebungsstrom zusätzlich zu dem Anteil durch die Änderung der Feldstärke aus sich tatsächlich bewegenden Ladungen des Materials. Diese Ladungen sind aber nicht frei beweglich, sodass das Material polarisiert wird. Bei kleinen Feldstärken wächst die Polarisation linear. Dann wird der Einfluss des Isolators beschrieben durch seine Dielektrizitätszahl und die gespeicherte Ladung ist proportional zur Spannung. Die Proportionalitätskonstante wird als Kapazität bezeichnet; sie ist das wesentliche Merkmal eines Kondensators. Je größer die Kapazität ist, desto mehr Ladung und Energie kann ein Kondensator bei einer bestimmten Spannung speichern. Die Gleichungen

$Q = C \cdot U$

und

$W = \frac{1}{2}\cdot C\cdot U^2$

fassen das zusammen. Q ist die Ladung (in Coulomb, C, oder Amperesekunden, As), C die Kapazität (in Farad, F) und U die Spannung (in Volt, V); die Energie ist mit Arbeit W (in Joule, J) bezeichnet um sie von der Feldstärke E zu unterscheiden.

Wichtig ist die Maximalspannung, die ein Kondensator zwischen seinen Elektroden ertragen kann. Diese Spannungsfestigkeit sowie weitere Merkmale werden weiter unten besprochen.

Die für viele Anwendungen wichtige Entladedifferentialgleichung befindet sich im Artikel RC-Glied.

Geschichte

Leidener Flasche

Leidener Flasche

→ Hauptartikel: Leidener Flasche

Die Leidener Flasche ist die älteste Bauform eines Kondensators (Kapazität etwa 5 nF). Sie besteht aus einem Glasgefäß, das innen und außen mit Metallfolie, meist aus Aluminium, belegt ist. Das Glas wirkt als Isolator, später „Dielektrikum“ genannt. Das Prinzip der Leidener Flasche wurde unabhängig voneinander 1745 von dem Domdechanten Ewald Jürgen Georg von Kleist in Cammin (Pommern) und ein Jahr später von dem Physiker Pieter van Musschenbroek in Leiden gefunden, als sie bei Laborversuchen mit Anordnungen von Gläsern und Metallteilen elektrische Stromschläge erlitten.

Die Leidener Flasche und ähnliche Laborgeräte wurden in der Folge vornehmlich zur publikumswirksamen Demonstration von Stromschlägen (auch als „Kleistscher Stoß“ bekannt geworden) eingesetzt, bei später zunehmenden Kenntnissen über das Wesen der Elektrizität auch als Stromquelle für fortgeschrittenere Experimente: Benjamin Franklin verband eine Leidener Flasche über eine Metallschnur mit einem Drachen, den er in den Himmel steigen ließ. Es gelang ihm mit diesem gefährlichen Experiment, Ladung von Gewitterwolken auf die Leidener Flasche zu übertragen. Er prägte den Begriff „electrical condenser“.

Weiterentwicklung

Ein verbesserter Kondensator wurde 1775 durch Alessandro Volta (1745–1827) erfunden, er nannte ihn „electrophorous“ (Elektrophor, Elektrizitätsträger). Er bestand aus zwei Metallplatten, die durch eine Ebonitschicht gegeneinander isoliert waren. Man kann diese Anordnung bereits als Prototyp moderner Kondensatoren betrachten. Der Einsatz besserer Dielektrika führte später zu einer Reduzierung der Baugröße. Etwa 1850 wurde Glimmer, ein natürlich vorkommendes Mineral, in Scheiben geschnitten und als Isolator verwendet; kommerziell wurden diese Kondensatoren ab der Zeit des ersten Weltkrieges hergestellt. Gewickelte Papierkondensatoren mit Metallfolienbelägen sind seit 1876 in Gebrauch.^[2]

Kondensatoren, die durch den chemischen Aufbau eines äußerst dünnen Dielektrikums aus nichtleitendem Aluminiumoxid auf einer Aluminium-Anode und Verwendung eines flüssigen Elektrolyten zu Kondensatoren mit höherer Kapazität führten, die späteren „Elektrolytkondensatoren“, wurden 1896 von Charles Pollak zum Patent angemeldet^[3], sie wurden anfangs als Siebkondensator zur Unterdrückung von Brummgeräuschen in Telefonnetzen benutzt.

Seit etwa 1900 wurde auch Porzellan als Dielektrikum in Kondensatoren verwendet. Erst in den 1930er Jahren erfolgte durch die Erforschung weiterer keramischer Werkstoffe als Ersatz für Porzellan und Glimmer die Entwicklung der Keramikkondensatoren.

Mit der Entwicklung hochwertig isolierender Kunststofffolien aus dem Bereich der organischen Chemie nach dem Zweiten Weltkrieg begann die Industrie, das Papier in den Metall-Papierkondensatoren durch dünnere und spannungsfestere Kunststofffolien zu ersetzen, aus denen sich eine breite Palette von unterschiedlichen Kunststoff-Folienkondensatoren entwickelte.

Ebenfalls nach dem Zweiten Weltkrieg, ab etwa 1950, wurde bei der General Electric in den USA mit der Entwicklung von Tantal-Elektrolytkondensatoren begonnen. Hier gelang es, nicht nur eine Miniaturisierung durch eine erheblich höhere Kapazität pro Bauvolumen gegenüber den bislang bekannten Kondensatoren zu erreichen, sondern mit der Entwicklung eines festen Elektrolyten konnte außerdem die Langzeitstabilität von Elektrolytkondensatoren deutlich verbessert werden.

Eine nochmals deutliche Kapazitätssteigerung gelang mit dem von General Electric 1957 patentierten „low voltage electrolytic capacitor“,^[4] der durch SOHIO und ab 1971 durch NEC zu einem marktreifen Bauelement weiterentwickelt wurde und später die treffende Bezeichnung „Doppelschicht-Kondensator“ erhielt.

Eine neuere Entwicklung sind Silizium-Kondensatoren. Diese resultieren aus der großen Erfahrung der Halbleiterindustrie mit der Strukturierung von Silizium und bieten dem Anwender frequenzstabile Kapazitätswerte bis in den Gigahertz-Bereich.

In den letzten Jahren erfolgte bei allen dafür geeigneten Kondensatorarten eine Entwicklung zu immer kleinerem Bauvolumen und hin zu oberflächenmontierbaren (SMD) Kondensatoren. Darüber hinaus wurde speziell bei Aluminium- und Tantal-Elektrolytkondensatoren durch Einführung von neuen Polymer-Elektrolytsystemen eine erhebliche Erhöhung der Elektrolyt-Leitfähigkeit und entsprechend geringere Verlustwiderstände erreicht.

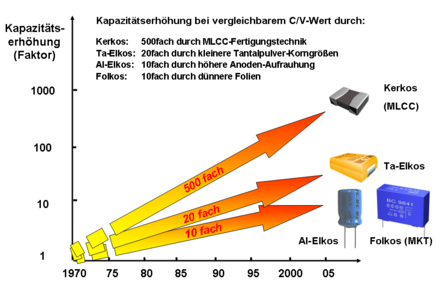Die Miniaturisierung in der Elektronik wurde nicht zuletzt auch durch Miniaturisierung bei den Kondensatoren erreicht. Die Volumeneffizienz eines Keramikkondensators beispielsweise konnte durch Weiterentwicklung in der Fertigungstechnik hin zu MLCC-Keramikkondensatoren bei gleichem C/V-Wert um etwa den Faktor 500 gesteigert werden.

Kondensatoren werden in einer Vielzahl von Geräten eingesetzt, sie hatten 1998 ein Marktvolumen von 9,2 Milliarden Dollar, wobei 38 % Keramikkondensatoren und 28 % Elektrolytkondensatoren einnahmen. Der Rest verteilte sich überwiegend auf Folien- und Papierkondensatoren.^[5]

Aktuelle (2009) Forschungen beschäftigen sich unter anderem mit neuen Oberflächenstrukturierungen der Elektroden. Beispielsweise lässt sich durch eine Nanostruktur in Form von Milliarden nebeneinander liegender kleiner Löcher in einer dünnen Aluminiumschicht, beschichtet mit Titan-Nitrid/Aluminiumoxid/Titan-Nitrid als kapazitiver Aufbau, die Leistungsdichte eines Nanokondensators, gemessen in W/kg, um mehr als das Zehnfache gegenüber Elektrolytkondensatoren vergrößern und erreicht damit eine Speicherfähigkeit in der Größenordnung von Doppelschichtkondensatoren, ohne deren Nachteil, die begrenzte Lade- bzw. Entladegeschwindigkeit aufzuweisen.^[6][7][8][9]

Berechnung der Kapazität

→ Hauptartikel: Elektrische Kapazität

Einfacher Plattenkondensator aus dem Physikunterricht

Für eine Reihe von idealisierten Elektrodenanordnungen lässt sich die Feldverteilung E(r) im Kondensator und damit seine Kapazität C exakt bestimmen. In der folgenden Tabelle sind einige wichtige Anordnungen aufgeführt:

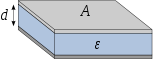
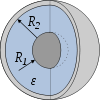
Bezeichnung	Kapazität	Elektrisches Feld	Schematische Darstellung
Plattenkondensator	$C=\varepsilon_0\varepsilon_r \cdot { {A} \over {d} }$	$E=\frac{Q}{\varepsilon_0 \varepsilon_r A}$
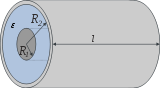
Zylinderkondensator	$C=2\pi \varepsilon_0\varepsilon_r \frac{l}{\ln(\frac{R_2}{R_1})}$	$E(r)=\frac{Q}{2\pi r l \varepsilon_0 \varepsilon_r}$
Kugelkondensator	$C=4 \pi \varepsilon_0 \varepsilon_r \left( \frac{1}{R_1}-\frac{1}{R_2}\right)^{-1}$	$E(r)=\frac{Q}{4\pi r^2 \varepsilon_0 \varepsilon_r}$
Kugel	C = 4πε0εrR1

Hier bezeichnet ggf. A die Elektrodenfläche, d deren Abstand, l deren Länge, R₁ sowie R₂ deren Radien. In der schematischen Darstellung sind die Elektroden hellgrau bzw. dunkelgrau und das Dielektrikum blau gefärbt. Anzumerken ist hier, dass bei den Anordnungen Plattenkondensator und Zylinderkondensator nur der Kapazitätsanteil durch dieses blau dargestellte Dielektrikum berechnet wird. Da auch Felder außerhalb des dargestellten Dielektrikums existieren – die bildlich gesprochen seitlich herausquellen –, stellen die gegebenen Formeln nur Näherungen dar, die umso besser werden, je geringer der Abstand der Elektroden im Vergleich zu ihrer Länge ist.

Aufbau eines Vielschichtkondensators: Das Dielektrikum ist blau, die mit einem Potentialanschluss verbundenen Elektroden sind dunkelgrau, mit dem anderen hellgrau dargestellt.

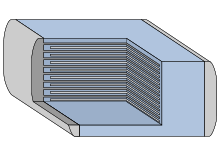
Plattenkondensatoren erlauben in einer modifizierten Ausführung sehr hohe Kapazitäten pro Volumen: Indem man die jeweils mit einem Potential verbundenen Elektroden abwechselnd aufeinander gestapelt, werden sie doppelt wirksam. Die Abbildung des Vielschichtkondensators verdeutlicht dies. Sind die Platten als Metallfolie oder -film ausgeführt, können sie bei einem geeigneten Isolator auch aufgewickelt werden, auch dabei verdoppelt sich die Wirkung. Aufgrund seiner kompakten Bauform ist das der gebräuchlichste Kondensator.

Zylinderkondensatoren werden meist nur bei speziellen Anwendungen eingesetzt, beispielsweise als Vakuum- oder Durchführungskondensator. Die für die Bauform angegebene Gleichung ist aber auch hilfreich, um den Kapazitätsbelag einer Koaxialleitung zu bestimmen.

Bei Kugelkondensatoren ist insbesondere der Spezialfall, $R_2 \to \infty$ von Bedeutung, die Kapazität einer freistehenden Kugel. Hier wird die Gegenelektrode durch die Umgebung gebildet, sie liegt deshalb gewöhnlich auf Erdpotenzial. Die Kapazität dieser Bauform ist sehr gering. So hat eine Kugel mit einem Radius von 15 cm, wie sie im Van-de-Graaff-Generator zur Ladungsspeicherung oder in Tesla-Spulen zur Bildung eines LC-Schwingkreises eingesetzt wird, theoretisch eine Kapazität von ca. 16,7 pF. In der Praxis ist die Kapazität jedoch höher, weil die Gegenelektrode (Erde) nicht unendlich weit entfernt ist. Im CGS-Einheitensystem ist die Kapazität eines Kugelkondensators gleich dem Radius der Kugel in Zentimetern, die oben genannte Kugel hat also eine Kapazität von 15 cm. Da auf der Kugeloberfläche das elektrische Feld sehr homogen ist, können Kugelkondensatoren auf mehrere Millionen Volt aufgeladen werden, bevor es zu einer Funkenentladung kommt.

Anwendungen

Energie- und Ladungsspeicher

Eine typische Anwendung in der Leistungselektronik bilden Zwischenkreiskondensatoren in Schaltnetzteilen und Umrichtern. Hier übernimmt eine Schaltung (zum Beispiel Gleichrichter, Vierquadrantensteller) die Gleichrichtung von Wechselstrom, dieser Schaltungsteil agiert als Stromquelle. Ein zweiter Schaltungsteil agiert als Senke (zum Beispiel Wechselrichter). Der Zwischenkreiskondensator hat die Aufgabe, den pulsierenden Strom aus dem Gleichrichter aufzunehmen und dem Wechselrichter eine ausreichend konstante Spannung zuzuführen. Je größer seine Kapazität desto kleiner die Spannungsänderung durch die Stromentnahme zwischen den Ladepulsen. Die gleiche Funktion haben auch die Glättungskondensatoren am Ausgang von Gleichspannungswandlern und in Gleichspannungsnetzteilen, sie halten deren Brummspannung möglichst klein.

In ähnlicher Weise können Kondensatoren zeitlich begrenzt hohe Leistung bereitstellen (siehe auch Doppelschichtkondensator). Sie werden auf eine bestimmte Spannung aufgeladen und können dann Verbraucher mit hohem kurzzeitigem Leistungsbedarf antreiben. Beispiele dafür sind die Hochspannungs-Kondensatorzündung bei Verbrennungsmotoren und in der Waffentechnik der „exploding-bridgewire detonator“^[10].

Eine typische Anwendung findet man in Blitzlichtgeräten. Ein Kondensator wird mit Hilfe eines Spannungswandlers innerhalb von einigen Sekunden aus einer Batterie bis etwa 400 V aufgeladen. Nach Zündung der Blitzröhre entlädt sich der Kondensator innerhalb einiger Mikrosekunden und liefert dabei eine Leistung von einigen Kilowatt. Die Batterie selbst kann wegen ihres hohen Innenwiderstandes unmöglich so viel Leistung zur Verfügung stellen.

Gleiches gilt für die heute in der Medizin eingesetzten Defibrillatoren. Implantierbare Defibrillatoren arbeiten mit Spannungen von zirka 650 bis 800 V und einer Schockenergie von 30 J bei einer Batteriespannung von zirka 3,5 V. Die Kapazitäten der Kondensatoren liegen bei etwa 100 bis 170 μF.

Stützkondensatoren dienen zur Stabilisierung der Versorgungsspannung in hochfrequenten und komplexen digitalen Schaltungen. Hier werden zu jedem IC oder Schaltungsabschnitt ein oder mehrere Kondensatoren parallel zur Versorgungsspannung geschaltet, die als Spannungs- oder Energiequelle in Momenten hohen Strom- bzw. Leistungsbedarfs wirken. Durch ihre niedrige Impedanz bei hohen Frequenzen verringern sie die Impedanz der übergeordneten Spannungsversorgung oder deren Zuleitung und verhindern eine gegenseitige Beeinflussung der Energieversorgung von Teilschaltungen. Umgekehrt können Kondensatoren störende, zeitlich begrenzte Überspannungen in elektronischen Schaltungen aufnehmen und so ihre Ausbreitung und schädliche Wirkung verhindern. Man nennt das Glätten oder Abblockung und bezeichnet jene Bauteile als Glättungs- oder Blockkondensatoren. Entstehen die Überspannungen durch Schaltvorgänge an Relais oder Leistungshalbleitern, werden die Kondensatoren speziell als Lösch- bzw. Snubberkondensatoren bezeichnet.

Des Weiteren werden Verschaltungen von mehreren Kondensatoren zum Herauf-, Herabsetzen und zum Invertieren von Versorgungsspannungen genutzt. Hier werden Kondensatoren zyklisch auf ein Potential aufgeladen, mit einem anderen Potential verbunden und dort entladen. Gebräuchliche Schaltungen sind die Ladungspumpe und deren spezielle Ausführung als Hochspannungskaskade.

Für Anwendungen, in denen es nicht auf schnellste Verfügbarkeit ankommt, sind zur Speicherung größerer Energiemengen andere Speichertechnologien wirtschaftlicher.

Frequenzabhängiger Widerstand

Für die Anwendung als frequenzabhängiger Blindwiderstand muss der Kondensator eine bekannte Kapazität haben, da der Kapazitätswert direkten Einfluss auf den kapazitiven Blindwiderstand hat. Im folgenden werden Anwendungen des frequenzabhängigen Blindwiderstandes genannt, wie sie in der elektrischen Energietechnik, Nachrichtentechnik, Analog- und Digitaltechnik auftreten.

Energietechnik

In der Energietechnik werden spezielle Leistungskondensatoren dazu genutzt, um die Phasenlage zwischen Strom und Spannung eines Wechselstromes zu ändern: Werden in mittleren und großen Industrie- und Werksanlagen viele leistungsstarke Elektromotoren, Leuchtstoffröhrendrosseln und Transformatoren betrieben, kommt es aufgrund von deren Gesamtinduktivität zu einem erheblichen induktiven Blindstrom, der bei Nichtkompensation die Energierechnung drastisch erhöhen und außerdem größere Leitungsquerschnitte der Stromleitungen innerhalb der Energieverteilung des Werkes bis hin zum Elektrizitätswerk erzwingen würde. Die induktiven „Phasenverschiebungen“ der Motoren und Trafos werden je nach aktueller Phasenlage, was proportional der gerade in Betrieb befindlichen induktiven Verbraucher entspricht, innerhalb der Werksenergieverteilung durch die Zu- oder Abschaltung von einzelnen oder ganzen Kondensatorgruppen automatisch kapazitiv kompensiert. Bei kleineren Elektromotoren erfolgt die Blindstrom-Kompensation durch einen Kondensator meist schon direkt am Motor. Für eine effektive Blindstromkompensation müssen die Kompensationskondensatoren und die Motor- und Trafoinduktivitäten immer möglichst die gleiche gegenphasige Impedanz haben, d.h. der Leistungsfaktor wird am Stromübergabepunkt des Elektrizitätswerkes in der Werksenergieverteilungszentrale möglichst immer bei 1 gehalten.

Eine weitere Anwendung findet der Kondensator in einem Kondensatormotor, bei dem er zusammen mit einer Feldspule des Motors die Phasenlage des Wechselstroms verschiebt, wodurch letztendlich ein magnetisches Drehfeld erzeugt wird. Durch einen externen Phasenschieberkondensator kann z.B. auch ein Dreiphasenmotor (L1, L2, L3) unter Wirkleistungseinbuße unter Beachtung der Betriebsspannung am Einphasenstromnetz (L, N oder L, L) betrieben werden.

Zur Herabsetzung von Spannungen bzw. als kapazitiver Vorwiderstand an Stelle eines wärmeerzeugenden reale Widerstandes oder eines teuren Transformators wird der Kondensator in einem Kondensatornetzteil verwendet: er arbeitet dort an einer großen Wechselspannung (in der Regel die Netzspannung) und liefert einen kleinen Wechselstrom, der z.B. an einer Zenerdiode zusammen mit einer normalen Rückstromdiode eine abgreifbare Spannung erzeugt, die dann in einer nachfolgenden Schaltung als Versorgungsspannung genutzt werden kann. Allerdings entfällt hier die galvanische Trennung zwischen Netz- und Verbraucherstromkreis.

Filteranwendungen

Die Frequenzabhängigkeit des Wechselstromwiderstands wird benutzt, um Wechselspannungen frequenzabhängig anzuheben oder abzusenken, zu „filtern“. Eine einfache Schaltung ist das RC-Glied, das je nach Schaltung als Hoch- oder Tiefpass wirkt. Einen Grenzfall des Hochpasses stellt der Koppelkondensator dar, der dazu dient, Gleichströme von überlagerten, höherfrequenten Wechselstromanteilen zu trennen. Das ist unter anderem nötig, um den Arbeitspunkt bei Analog-Verstärkern einstellbar zu halten.

Zusammen mit Spulen, die als Kenngröße eine bestimmte Induktivität aufweisen, ohmschen Widerständen und eventuell aktiven Bauelementen werden Kondensatoren in elektronischen Schaltungen auch für Schwingkreise, Bandfilter und Frequenzweichen verwendet. Dabei ergibt sich eine bestimmte Resonanzfrequenz. Entsprechende Schaltungen sind ebenfalls Hoch- oder Tiefpässe, lassen sich allerdings mit höherer Güte herstellen. Ein Beispiel dafür sind die Frequenzweichen in Lautsprechern.

Eine zeitdiskrete Variante von speziellen Filtern, die Kondensatoren in ihrem Aufbau verwenden, stellen die Switched-Capacitor-Filter dar. Weiters können in Filtern Spulen durch sogenannte Gyratoren nachgebildet werden: Dabei wird mit der Kapazität eines Kondensators unter Verwendung einer aktiven Schaltung die Induktivität einer Spule nachgebildet.

Wandler

Die sich an einem Kondensator aufbauende Spannung ist proportional dem Integral des Ladestromes über die Zeit. Auf diese Weise werden Kondensatoren zur Festlegung von Schaltzeiten genutzt, zum Beispiel bestimmt ein Kondensator die Schaltzeiten einer astabilen Kippstufe. Dazu wird ein Kondensator über eine Stromquelle geladen; seine Spannung nimmt proportional zur verstrichenen Zeit zu. Sobald die Spannung einen bestimmten Wert überschreitet, erfolgt ein Zustandswechsel der Schaltung. In ähnlicher Weise wird eine Reihe von Wandlerschaltungen realisiert:

• Spannungs-Frequenz-Wandler: Diese Schaltung wandelt eine Eingangsspannung in eine dazu proportionale Frequenz um. Ein Kondensator wird zyklisch durch eine spannungsgesteuerte Konstantstromquelle bis zu einer vorgegebenen Spannung geladen, dann schlagartig entladen. Die Frequenz des sägezahnförmigen Spannungsverlaufes am Kondensator ist das Ausgangssignal.
• Analog-Digital-Umsetzer nach dem slope-Prinzip: Dieser Wandler gleicht dem Spannungs-Frequenz-Wandler, arbeitet allerdings nicht zwingend zyklisch.
• Zeitmessung: Hier wird die Stromquelle durch einen Impuls unbekannter Länge gesteuert, die Spannung des Kondensators nach dem Impulsende ist proportional zur Impulslänge.
• Frequenz-Spannungs-Wandler: Zur Frequenzmessung werden im Takt der zu messenden Frequenz Impulse konstanter Länge erzeugt. Diese laden periodisch einen Kondensator, dem ein konstanter Entladestrom entnommen wird. Die Spannung am Kondensator ist das Ausgangssignal.

Informationsspeicher

Der Ladungszustand eines Kondensators kann Information in digitaler oder analoger Form repräsentieren. Analoge Informationsspeicherung mittels eines Kondensators findet beispielsweise in der Abtast-Halte-Schaltung statt: während der Abtastphase wird ein Kondensator mit einer Eingangs-Signalspannung verbunden, von welcher er während der Haltephase getrennt wird. Der Spannungswert steht dann zur Weiterverarbeitung, typischerweise einer Analog-Digital-Wandlung (ADC), konstant zur Verfügung. Eine andere Art analoger Informationsspeicherung ist der Eimerkettenspeicher.

Zur Speicherung von großen Informationsmengen können einige Milliarden Kondensatoren in einer integrierten Schaltung zusammengefasst werden. Beispiele dafür sind dynamisches RAM (DRAM), Eraseable Programmable Read Only Memory (EPROM) und Flash-Speicher.

Kondensatoren als Sensoren

Sonderbauformen von Kondensatoren sind als Sensoren für eine Reihe physikalischer Größen geeignet. Diese Größen bewirken eine Änderung der Kapazität oder der enthaltenen Ladung, beides kann durch eine nachfolgende Schaltung ausgewertet werden. Man kann die Messprinzipien in die beiden folgenden Gruppen einteilen:

Änderung der Elektrodengeometrie

Die Kapazität eines Kondensators ändert sich mit dem Abstand der Elektroden. So können Kondensatoren zur Abstands- und Dickenmessung verwendet werden, indem eine Elektrode mit der Messgröße mechanisch gekoppelt wird und sich so die Veränderung der Messgröße auf eine Veränderung des Plattenabstandes überträgt. So können zum Beispiel Lackschichtdicken oder der Abstand einer Düse bei der Laser-Materialbearbeitung bestimmt werden. In diese Gruppe gehören auch der kapazitiver Näherungsschalter und der kapazitive Touchscreen. Bei letzterem wird der Abstand zum Finger ortsaufgelöst ausgewertet.

Auch Beschleunigung kann auf diese Weise erfasst werden: Aufgrund der Massenträgheit einer beweglichen Elektrode zum Beispiel in einem mikromechanischen Beschleunigungssensor ändert eine Beschleunigung den Abstand zwischen den Elektroden eines Kondensators. In ähnlicher Art sind Sensoren für Druck und Druckänderung (Manometer) aufgebaut: Ein kompressibles Dielektrikum, meist Luft, bewirkt, dass eine Druckänderung eine Abstandsänderung der Platten hervorruft. Nach diesem Prinzip funktioniert auch das Kondensatormikrofon, das den Schalldruck oder den Schalldruckgradienten in ein elektrisches Signal wandelt. Dessen Umkehrung ist der Kondensatorlautsprecher.

Alternativ kann eine Messgröße auch die Überdeckung der Elektroden verändern, wodurch sich ebenfalls die Kapazität ändert. So lassen sich bspw. Winkel messen, indem kreissegmentförmige Elektroden gegeneinander verdreht werden, ähnlich dem weiter unten beschriebenen Drehkondensator.

Änderung des Dielektrikums

Die zumeist störende Eigenschaft des Dielektrikums, unter Einfluss von ionisierender Strahlung seine Leitfähigkeit zu erhöhen, wird bei der Steuerung der Belichtungszeit von Röntgenfilmen genutzt. Dazu liegt im Strahlengang ein Kondensator, der vor der Aufnahme eine der Filmempfindlichkeit proportionale Ladung erhält. Sobald die Ladung während der Aufnahme einen bestimmten Wert unterschreitet, wird die Belichtung abgebrochen.

Ähnlich funktionieren manche Brandmelder, bei denen ein radioaktives Präparat verwendet wird, dessen ionisierende Wirkung durch die Rauchgase abgeschwächt wird. CCD-Sensoren als Bildaufnehmer nutzen den gleichen Effekt: Die Leitfähigkeit eines Halbleiters wird durch Lichteinstrahlung erhöht und die Ladung abgebaut. Bei einem kapazitiven Hygrometer beeinflusst die Luftfeuchtigkeit die Dielektrizitätszahl eines speziellen Isolationsmaterials und auf diese Weise die Kapazität.

Ebenfalls auf einer Änderung der Dielektrizitätszahl beruht der kapazitive Füllstandssensor. Hier sind die Elektroden so befestigt, dass sie mit zunehmenden Füllstand weiter in die Flüssigkeit eintauchen. Durch die höhere Permittivität der Flüssigkeit nimmt die Kapazität mit zunehmender Tauchtiefe zu.

Bauarten und Bauformen

Im Laufe der Historie der Kondensatoren haben sich viele industriell genutzte Bauarten, auch Familien oder Technologien genannt, entwickelt. Diese werden gemäß der Eingruppierung in den internationalen und nationalen Normen in Kondensatoren mit fester Kapazität, die „Festkondensatoren“, und Kondensatoren mit veränderbarer Kapazität, die „Veränderbaren oder Variablen Kondensatoren“, unterteilt.

Kondensatoren mit fester Kapazität, Festkondensatoren

Kondensatoren zur Montage auf Platinen.
Obere Reihe, radiale Anschlüsse (v.l.): Glimmer, Keramik-Y, Keramik-Scheibe, Keramik-Mehrschicht, Folie gewickelt und vergossen, geschichteter Folienkondensator, gewickeltes und vergossenes Polystyrol, gewickelter X-Metallpapierkondensator, dito hochkant (man sieht die großflächige Kontaktierung der Stirnseiten), zwei Tantal-, zwei Aluminiumelektrolytkondensatoren, Doppelschichtkondensator
Mittlere Reihe, axiale Anschlüsse: gewickelter Polypropylen-, Polystyrol-Folienkondensator, Keramik-Durchführungskondensator, bipolarer Elektrolytkondensator.
Untere Reihe, SMD-Bauformen: zwei SiO₂-, zwei Keramikkondensatoren, zwei Folienkondensatoren, Durchführungskondensator sowie SMD-Tantal- und Aluminium-Elektrolytkondensatoren.

Festkondensatoren haben einen definierten und mit einer Toleranz versehenen Kapazitätswert. Es gibt sie je nach den technischen Anforderungen wie z. B. Spannungsfestigkeit, Strombelastbarkeit, Kapazitätsstabilität, Temperaturkoeffizient, Einsatzfrequenzbereich, Temperaturbereich oder Montageart (SMD-Ausführung) sowie nach wirtschaftlichen Anforderungen (Preis) in zahlreichen verschiedenen Technologie-Familien, Ausführungen und Bauformen.

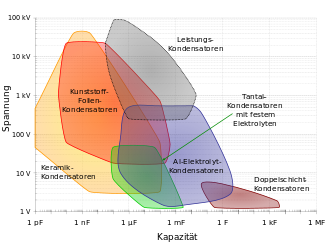
Die wichtigsten industriellen hergestellten Festkondensatoren sind Keramik-, Kunststoff-, Elektrolyt- und Doppelschicht-Kondensatoren. Keramik- und Kunststoff-Folienkondensatoren besitzen Kapazitätswerte im Bereich weniger Pikofarad bis zu etwa 100 Mikrofarad. Elektrolytkondensatoren beginnen bei etwa 1 Mikrofarad und erstrecken sich bis in den Farad-Bereich. Darüber hinaus haben Doppelschicht-Kondensatoren Kapazitätswerte bis in den Kilofaradbereich.

Keramikvielschicht- Chipkondensatoren unterschiedlicher Größe zwischen Keramik-Scheibenkondensatoren

Keramikkondensator

Keramikkondensatoren haben keramische Dielektrika mit Spannungsfestigkeiten von 10 bis zu 100.000 V bei verschieden hoher Permittivität. Sie bilden eine große Gruppe von Kondensatoren im unteren Kapazitätsbereich (0,5 pF bis zu 100 µF oder mehr). Die verwendeten Keramikarten gehören einerseits zu den paraelektrischen Materialien mit feldstärkeunabhängiger relativer Permittivität, beispielsweise Titandioxid (TiO₂), andererseits zu den ferroelektrischen Materialien mit feldstärkeabhängiger relativer Permittivität, wie zum Beispiel Bariumtitanat (BaTiO₃). Keramikkondensatoren werden aus fein gemahlenen Granulaten durch Sinterung im Temperaturbereich zwischen 1200 und 1400 °C hergestellt. Durch geeignete Zusatzstoffe (Aluminium-Silikate, Magnesium-Silikate. Aluminiumoxide) kann die relative Permittivität ε_r eines Keramikkondensators zwischen 6 und 14.000 liegen. Die Keramikkondensatoren werden anhand ihrer Keramikart und damit zusammenhängend ihren elektrischen Eigenschaften in zwei Klassen eingeteilt: Klasse-1-Kondensatoren, die sich für Hochfrequenz- und Filteranwendungen eignen und Klasse-2-Kondensatoren, die als Energiespeicher und Siebkondensator eingesetzt werden.

Kunststoff-Folienkondensator

Gebecherte und tauchlackierte Kunststoff-Folienkondensatoren

Kunststoff-Folienkondensatoren verwenden Folien aus Kunststoff oder Kunststoffmischungen als Dielektrikum und werden in zwei Ausführungen hergestellt:

• Kunststoff-Folienkondensatoren mit Metallbelägen bestehen aus je zwei Kunststofffolien, die beide mit einer Metallfolie, meist aus Aluminium, belegt sind und gemeinsam zu einem Wickel aufgerollt werden. Bei den üblichen kleineren Bauformen ragen die Metallfolien abwechselnd entgegengesetzt über die Kunststofffolie hinaus, so dass auf jeder Seite des Wickels eine der Metallfolien übersteht, die dann großflächig und induktionsarm mit dem jeweiligen Anschluss kontaktiert wird.
• Metallisierte Kunststoff-Folienkondensatoren bestehen im einfachsten Fall aus zwei Kunststofffolien, die jeweils einseitig mit Aluminium bedampft sind. Diese werden mit leichtem seitlichem Versatz so aufgewickelt, dass die metallisierten Folien an gegenüberliegenden Seiten aus dem Wickel heraus stehen und somit kontaktiert werden können. Diese Bauform gibt es auch als Schichtkondensatoren – die Lagen werden zu einem großen Block geschichtet, aus dem die einzelnen Kondensatoren herausgesägt werden. Metallisierte Kunststoff-Folienkondensatoren sind, wie MP-Kondensatoren, bei einem Durchschlag selbstheilend, da die dünne Metallschicht der Beläge vom Spannungsdurchschlags-Lichtbogen um den Durchschlagskanal herum verdampft.

Metallpapierkondensator

Metallpapierkondensatoren (MP-Kondensatoren) bestehen aus je zwei mit Aluminium metallisierten Papierstreifen (Isolierpapier), die mit einer weiteren Papierfolie zu einem Wickel aufgerollt und in einem Becher eingebaut werden. Der Wickel wird mit einem Isolieröl imprägniert, wodurch die Spannungsfestigkeit erhöht und der Verlustfaktor verringert wird. MP-Kondensatoren finden vor allem als Leistungskondensatoren im Bereich der Leistungselektronik und für Netzanwendung als Entstörkondensator Verwendung. Sie sind auf Grund der metallisierten Beläge, wie vergleichbare Kunststoff-Folienkondensatoren, selbstheilend.

Elektrolytkondensator

Verschiedene Bauformen von Tantal- und von Aluminium-Elektrolytkondensatoren

Elektrolytkondensatoren (auch Elko genannt) sind gepolte Kondensatoren, dessen Anoden-Elektrode aus einem Metall (Aluminium, Tantal und Niob) besteht, auf dem durch Elektrolyse (anodische Oxidation, Formierung) eine äußerst dünne, elektrisch isolierende Schicht aus dem Oxid des Anodenmetalls erzeugt wird, die das Dielektrikum des Kondensators bildet. Zur Vergrößerung der Oberfläche wird die Anode strukturiert, bei Aluminium-Elkos wird die Anodenfolie aufgeraut, bei Tantal- und Niob-Elkos wird Metallpulver zu einem schwammartigen Körper gesintert. Der Elektrolyt kann aus einem flüssigen Elektrolyten (Ionenleiter) oder einem festen Elektrolyten (Elektronenleiter) bestehen und bildet die Kathode des Elektrolytkondensators, die sich der strukturierten Oberfläche der Anode perfekt anpassen muss. Die Stromzuführung zum Elektrolyten erfolgt über Folien gleichen Metalls wie das der Anode oder über eine andere geeignete Kontaktierung. Elektrolytkondensatoren sind, mit Ausnahme bipolarer Elektrolytkondensatoren, immer gepolte Bauelemente, die Anode ist der positive Anschluss. Sie dürfen niemals mit falsch gepolter Spannung betrieben werden (Explosionsgefahr) und können schon bei geringer Überspannung zerstört werden. Zur besseren Verpolungssicherheit gibt es Bauformen mit drei Pins, welche in Form eines unregelmäßigen Dreiecks angeordnet sind und daher nur in einer bestimmten Position in die Platine gelötet werden können. Der dritte Pin ist je nach Hersteller entweder unbeschaltet, mit dem Gehäuse oder mit der Kathode verbunden. Durch gegenpolige Serienschaltung zweier Anodenfolien in einem Kondensatorgehäuse werden für spezielle Anwendungen (zum Beispiel Tonfrequenzweichen) auch Bipolar-Elektrolytkondensatoren für Wechselspannungsbetrieb hergestellt. Neueste Entwicklungen auf dem Gebiet der Elektrolytkondensatoren sind Aluminium- und Tantal-Elektrolytkondensatoren mit Polymer-Elektrolyte aus leitfähigen Polymeren, die sich durch besonders geringe interne ohmsche Verluste auszeichnen.

Doppelschichtkondensatoren

Doppelschichtkondensatoren bis 3000 F

Doppelschichtkondensatoren: (englisch electrochemical double layer capacitor, EDLC) sind gemeinsam mit den Pseudokondensatoren und den Hybridkondensatoren ein Teil einer neuen Familie von Kondensatoren, die unter dem Oberbegriff "Superkondensatoren" zusammengefasst werden. Sie haben die größte Energiedichte aller Kondensatoren. Ihre hohe Kapazität, bezogen auf das Bauvolumen, basiert einerseits auf dem physikalischen Phänomen äußerst dünner elektrisch isolierender Helmholtz-Doppelschichten an den Oberflächen spezieller großflächiger Elektrodenmaterialen, in denen die elektrische Energie statisch als Doppelschichtkapazität in elektrischen Feldern gespeichert wird. Andererseits stammt sehr oft ein weiterer Anteil an der hohen Kapazität aus einer sogenannten Pseudokapazität, einer innerhalb enger Grenzen spannungsabhängigen elektrochemischen bzw. faradayschen Speicherung elektrischer Energie, die mit in einer Redoxreaktion und mit einem Ladungsaustausch an den Elektroden verbunden ist, wobei allerdings im Gegensatz zu Akkumulatoren an den Elektroden keine chemische Stoffänderung eintritt. Die Pseudokapazität kann durch spezielle Elektroden bei gleichem Bauvolumen einen erheblich größeren Wert als die Doppelschichtkapazität erreichen.

Der jeweilige Anteil der Doppelschichtkapazität und der Pseudokapazität an der Gesamtkapazität des Kondensators wird in sehr grober Verallgemeinerung durch die Namensgebung solcher Kondensatoren in industriellen Veröffentlichungen erkennbar.

• Doppelschichtkondensatoren speichern die elektrische Energie überwiegend in Helmholtz-Doppelschichten ihrer Elektroden und haben keinen oder nur einen nur geringen Anteil (bis etwa 10 %) von Pseudokapazität an der Gesamtkapazität
• Superkondensatoren und Ultrakondensatoren weisen aufgrund ihrer Elektrodenkonstruktion mit hoher Redoxkapazität meist einen zum Teil deutlich höheren Anteil an der Pseudokapazität auf, wodurch sie eine höhere spezifische Kapazität als Doppelschichtkondensatoren haben.
• Hybridkondensatoren sind Superkondensatoren mit einer statischen Doppelschichtelektrode und einer elektrochemischen Redox-Elektrode, wobei die Redox-Elektrode einer Elektrode aus einer anderen Technologie, beispielsweise aus dem Bereich der Akkumulatoren oder der Elektrolytkondensatoren, ähneln kann.

Die neue Familie der Superkondensatoren umfasst Doppelschicht-, Pseudo- und Hybridkondensatoren

Allen Doppelschichtkondensatoren, Pseudokondensatoren, Superkondensatoren, Ultrakondensatoren und Hybridkondensatoren gemeinsam ist, dass der Elektrolyt die leitfähige Verbindung zwischen zwei Elektroden bildet. Das unterscheidet sie von Elektrolytkondensatoren, bei denen der Elektrolyt die Kathode bildet, der Elektrolyt also eine Elektrode ist, die mit dem negativen Anschluss des Kondensators verbunden ist.

Doppelschichtkondensatoren sind, wie auch Elektrolytkondensatoren, gepolte Bauelemente, die nur mit korrekter Polarität betrieben werden dürfen.

Doppelschichtkondensatoren, Superkondensatoren, Ultrakondensatoren und Hybridkondensatoren, zu denen die Lithium-Ionen-Kondensatoren zählen, werden unter vielen unterschiedlichen Handelsnamen wie z. B. BestCap, BoostCap, DLCAP, EVerCAP, DynaCap, Faradcap, GreenCap, Goldcap, SuperCap, PAS, PowerStor oder Ultracapacitor sowie die Lithium-Ionen-Kondensatoren unter Premlis, EneCapTen, Ultimo oder LIC angeboten.

Weitere Formen

Aufgesägter Vakuumkondensator

Vakuumkondensatoren

Sie sind bei großen hochfrequenten Strömen und Spannungen im Kilovolt-Bereich vorteilhaft und werden vorzugsweise bei Sendern hoher Sendeleistungen eingesetzt. Es gibt auch Bauformen mit variabler Kapazität. ^[11][12][13]

Glas-Dielektrikum

erlaubt einen hohen Temperaturbereich von −75 bis +200 °C; typische Werte sind 300 pF bis 100 nF. ^[14]

Kondensatoren auf Siliziumsubstrat

In integrierten Schaltkreisen werden Kondensatoren konventionell durch eine Schichtfolge von Silizium, Siliziumoxid, Aluminium hergestellt. Silizium und Aluminium bilden dabei die Elektroden des Kondensators; das Siliziumoxid (auch Siliziumnitrid) bildet das Dielektrikum. Sind besonders viele Kondensatoren erforderlich, wie in Halbleiterspeichern, so kommen auch schwieriger zu verarbeitende Dielektrika mit höherer Dielektrizitätszahl zum Einsatz. In besonderen Fällen, wenn der Speicherinhalt ohne Energieversorgung erhalten bleiben soll, auch Ferroelektrika.
Nach einem ähnlichen Verfahren werden auch diskrete Kondensatoren hergestellt, die bei Frequenzen bis in den Gigahertz-Bereich gute Eigenschaften besitzen. ^[15][16]

Glimmerkondensatoren

haben ein Dielektrikum aus dem natürlich vorkommenden Mineral Glimmer. Dieses weist eine hohe Spannungsfestigkeit auf und ist aufgrund seiner Schichtstruktur spaltbar in dünne Blättchen bis hinab zu 20 µm Dicke, die meist mit Silber als Elektrodenbeläge bedampft werden. Glimmerkondensatoren werden aufgrund der niedrigen Verlustfaktoren in der Sendetechnik und aufgrund ihrer hohen Kapazitätskonstanz und geringen Kapazitätstoleranz in Messnormalen und in Filter- und Schwingkreisanwendungen für hohe Anforderungen eingesetzt. Sie werden, nach dem englischen Wort für Glimmer, oft auch als Mica-Kondensatoren bezeichnet.

Neben der Unterteilung von Kondensatoren nach verwendetem Dielektrikum bzw. bei Elkos nach der Kathode kann auch eine Klassifizierung nach Anwendungsbereich oder nach Bauform erfolgen. Wichtige Beispiele sind:

Leistungskondensatoren

sind Metallpapier- oder Kunststoff-Folienkondensatoren. Sie können direkt an Versorgungsnetzspannung betrieben werden und zeichnen sich durch eine größere Bauform, je nach Leistungsbereich durch Steck- oder Schraubanschlüsse sowie meist durch erdbare Blechgehäuse aus und sind funktionell für eine hohe Strombelastbarkeit vorgesehen.^[17][18]

Durchführungskondensatoren

sind meist koaxial aufgebaute Kondensatoren, oft Keramikkondensatoren, die eine elektrische Leitung durch eine leitfähige Wandung (Abschirmung) führen. Der innen liegende Anschluss ragt beidseitig an den Enden eines leitfähigen Belags aus dem Kondensator heraus und bildet die Durchführung für eine elektrische Verbindung. Die außen liegende Elektrode des Kondensators wird mit der Wandung kontaktiert. Die Kapazität, die zwischen Innen- und Außenanschluss wirkt, leitet hochfrequente Störungen, zum Beispiel einkoppelnde Funkwellen aus der Umgebung, aus einer Geräte-Zuleitung gegen Masse ab.

Schutzringkondensatoren

sind eine spezielle Bauform eines Plattenkondensators um Randeffekte in Messvorgängen zu reduzieren.

Bauformen von Festkondensatoren

Die heutzutage industriell genutzten Bauformen von Festkondensatoren spiegeln die Entwicklung der industriellen Technik der letzten 100 Jahre wider. Die Bauformen zu Beginn des letzten Jahrhunderts wurden noch mechanisch mit Schrauben befestigt und die Anschlüsse per Hand gelötet oder auch angeschraubt. Der Preisdruck in der Fertigung führte Mitte des 20. Jahrhunderts zur Leiterplattentechnik. Dafür wurden bedrahtete Bauteile benötigt und die Kondensatoren wurden entsprechend mit Anschlussdrähten entwickelt. Aus zunächst liegenden Bauformen mit axialen Anschlüssen wurden, um Leiterplattenkosten einzusparen, dann etwas später radiale, stehende Bauformen. Diese werden häufig, bei gleichen elektrischen Werten, mit verschieden großen Abständen der Anschlüsse, dem Rastermaß (RM), angeboten.

Nochmals aus Kostengründen, denn die Bohrungen in der Leiterplatte sind auch eine Kostenfrage, diesmal aber auch verbunden mit der zunehmenden Miniaturisierung der Bauteile, begann in den 1990er Jahren der Siegeszug der oberflächenmontierbaren Bauelemente, der sog. „SMD“-Chips.

Bauformen von Kondensatoren

Neben den Bauteilen für das industrielle Massengeschäft finden sich aber auch weiterhin Bauformen, die sich aus speziellen Anforderungen der jeweiligen Schaltung ergeben. Beispielsweise die Flachbandanschlüsse von Folienkondensatoren für eine hohe Impuls-Strombelastbarkeit, die Schraubanschlüsse großer Aluminium-Elektrolytkondensatoren für hohe Strombelastbarkeit oder spezielle Bauformen für zum Beispiel Durchführungskondensatoren.

Auch Integrierte Schaltungen enthalten eine große Zahl von Kondensatoren. Je nach Anforderung können diese zwischen unterschiedlichen Schichten des ICs mit zwischenliegendem Isolator (= Dielektrikum) bestehen. Dieses können z. B. verschiedene Metall- oder Polysilizium-Schichten sein. Besonders bei DRAMs besteht jede Speichzelle üblicherweise aus einem Kondensator mit zugehörigem Transistor. Siehe auch: MIS-Kondensator.

Kondensatoren mit einstellbarer Kapazität

Einstellbare oder Variable Kondensatoren sind elektrische Kondensatoren, deren Kapazität in definierten Grenzen mechanisch stufenlos von Hand oder mit einer geregelten Motorsteuerung einstellbar ist. Sie werden unterschieden in Drehkondensatoren, kurz Drehkos genannt und in Trimmkondensatoren, auch Trimmer genannt. Neben den mechanisch einstellbaren Dreh- und Trimmkondensatoren gibt es Bauelemente mit elektrisch veränderbaren kapazitiven Eigenschaften, wie Kapazitätsdioden (Varicaps) und weitere, die als Sensoren (Winkelgeber, Näherungsschalter, Touchscreen) verwendet werden.

Drehkondensatoren

Beim Drehkondensator wird das Kondensatorprinzip der sich gegenüberliegenden Elektrodenplatten besonders deutlich. Hier abgebildet ist ein Zweifachdrehkondensator.

Mechanisch einstellbare Drehkondensatoren (Abk.: Dre(h)ko), auch Regel- oder Korrektionskondensatoren genannt, sind für häufige und wiederholende Betätigungen ausgelegt zum Beispiel für die manuelle Sendereinstellung in Rundfunkgeräten. Die Kapazitätsänderung bei Drehkondensatoren erfolgt durch Änderung der kapazitiv wirksamen Fläche, meist indem ein Elektrodenpaket, der Rotor, mit einer Welle mechanisch kammartig in ein zweites, feststehende Elektrodenpaket, den Stator, hineingedreht werden kann. Als Dielektrikum wird Luft, eine Kunststofffolie, ein Vakuum oder ein Schutzgas verwendet.

Drehkondensatoren für Kleinsignalanwendungen (Senderwahl und Schwingkreisabstimmung in Rundfunk- und Fernsehempfängern) sind heute weitgehend entweder durch Kapazitätsdioden abgelöst, deren Sperrschichtkapazität durch eine überlagerte Gleichspannung gesteuert wird oder sind durch VCO-gesteuerte PLL-Schaltungen ersetzt worden. Allerdings sind für Leistungsanwendungen mechanisch einstellbare Vakuum- und Schutzgaskondensatoren in Hochfrequenzsendern auch heutzutage (2009) durchaus noch im Einsatz, wobei die mechanische Betätigung zur Konstanthaltung einer Senderfrequenz meist über eine Motor-gesteuerte automatische Regelung erfolgt.

Vakuum- und Schutzgas-Drehkondensatoren

Vakuum- und Schutzgas-Drehkondensatoren ähneln konstruktiv den unter Variable Kondensatoren beschriebenen Tauchtrimmern. Umhüllt sind diese einstellbaren Kondensatoren mit einem hermetisch abdichtenden Glas- oder Keramikgehäuse.

Als Dielektrikum wird bei den variablen Vakuumkondensatoren ein Vakuum mit einer sehr hohen Spannungsfestigkeit, die im Mittel mit etwa 40 kV/mm angegeben wird, verwendet. Bei den variablen Schutzgas-Kondensatoren wird Schwefelhexafluorid SF₆ als Isoliergas eingesetzt. Es besitzt ebenfalls eine hohe Durchschlagsfestigkeit und darüber hinaus auch noch eine hohe Dielektrizitätszahl sowie gegenüber vielen Feststoffen kleinere dielektrische Verluste. Eingesetzt werden beide Arten dieser variablen Kondensatoren in Hochfrequenz-Sendern. Die größten und leistungsstärksten Kondensatoren dieser Art besitzen eine Vorrichtung zur Wasserkühlung.^[19]

Trimmer

Kunststoff-Folientrimmer

Trimmerkondensatoren (kurz Trimmer) sind ebenfalls stufenlos einstellbare Variable Kondensatoren, deren Kapazität in definierten Grenzen mechanisch einstellbar sind. Sie sind im Gegensatz zu Drehkondensatoren nicht für häufige Betätigung ausgelegt und werden nur zur Erstinbetriebnahme und ggf. nach Reparaturen betätigt, um einen schaltungstechnisch bedingten Kapazitätsausgleich eines Filters oder eines Schwingkreises in zum Beispiel Rundfunk- oder Fernsehgeräten herbeizuführen (Abgleich). Die Kapazitätsänderung bei einem Trimmer erfolgt durch Veränderung der kapazitiv wirksamen Fläche des Kondensators. Trimmerkondensatoren können oft nur mit einem isolierenden (HF-neutralen) Werkzeug, meist einem Plastik-Schraubendreher, eingestellt werden. Als Dielektrikum in Trimmkondensatoren wird Luft (Luftplatten- und Tauchtrimmer), Kunststofffolie, (Folientrimmer) und Keramik (Draht-, Rohr-, Scheiben- und SMD-Trimmer) verwendet. Trimmer für Kleinsignalanwendungen (Senderwahl und Schwingkreisabstimmung in Rundfunk- und Fernsehempfängern) sind heute weitgehend entweder durch Kapazitätsdioden abgelöst, deren Sperrschichtkapazität durch eine überlagerte Gleichspannung gesteuert wird oder sind durch VCO-gesteuerte PLL-Schaltungen ersetzt worden.

Die moderneren Bauformen von Trimmerkondensatoren sind oberflächenmontierbar. Die Keramik-SMD-Trimmer haben eine keramische Schichtung mit einer halbkreisförmigen Metallisierung in der Stator-Grundplatte und eine Rotorelektrode, die drehbar montiert ist. SMD-Trimmer für Lötwellenlötung sind, um Verschmutzungen während des Lötprozesses zu verhindern, gekapselt. Trimmer für Reflow-Lötung können etwas einfacher geschützt sein.^[20]

Bei der zweiten Trimmer-SMD-Bauform, den SMD-Abgleichkondensatoren, gibt es keine mechanisch bewegliche Einstellmöglichkeit mehr. Bei ihnen wird der Kapazitätswert durch gezieltes Wegbrennen von Flächenanteilen einer oben liegenden offen zugänglichen Elektrode mit Hilfe eines Laserstrahles eingestellt. Damit lässt sich gezielt gewünschter Kapazitätswert mit einer sehr großen Genauigkeit einstellen.^[21]

Kapazitätsdiode

Die Kapazitätsdiode, auch Varicap, Varaktor, Abstimmdiode oder Ladungsspeicherdiode genannt, ist ein elektronisches Halbleiter-Bauteil. Wird eine Diode in Sperrrichtung betrieben, so entsteht am p-n-Übergang eine Ladungsträgerverarmungszone (die als Dielektrikum wirkt), an der sich auch ein elektrisches Feld aufbaut. Mit steigender Spannung vergrößert sich die Breite der ladungsfreien Zone, damit nimmt die Kapazität ab. Durch Änderung der angelegten Spannung lässt sich eine elektrisch steuerbare Kapazität erreichen.

Kennzeichnungen

Bei Kondensatoren gibt es keine so einheitliche Kennzeichnung wie bei Widerständen. Einige häufige Varianten sind unten aufgelistet. Weitere Informationen sind über die Weblinks unten zu finden.

Kennzeichnung der Kapazität

• 473: Die ersten beiden Ziffern geben den Wert in Pikofarad an, die dritte die Anzahl der nachfolgenden Nullen. 473 bedeutet also 47 × 10³ pF = 47000 pF = 47 nF.
• 18: Oft auf keramischen bedrahteten Kondensatoren als Aufdruck zu finden, bedeutet eine Angabe in Pikofarad, hier also 18 pF.
• 3n9: Bedeutet 3,9 nF.
• .33 K 250: Die erste Zahl gibt den Wert in Mikrofarad an, also 0,33 µF = 330 nF. K steht für eine Kapazitätstoleranz von 10 % und 250 für die Spitzenspannung in Volt, die angelegt werden darf.
• Für die zunehmend seltener werdende axiale Bauform waren auch Farbcodes üblich.

Papierkondensator mit der Kapazität „5000 cm“.

Mitte des 20. Jahrhunderts wurden vor allem Papierkondensatoren, welche in den damals aufkommenden ersten Röhrenempfängern für den Rundfunkempfang eingesetzt wurden, häufig mit der Einheit „cm“ beschriftet, der Kapazitätseinheit im heute kaum noch gebrauchten elektrostatischen CGS-Einheitensystem.

Die nebenstehende Abbildung zeigt einen Papierkondensator der Firma SATOR aus dem Jahr 1950 mit einer Kapazität laut Aufdruck von „5.000 cm“ bei einer Prüfspannung von „2.000 V“. Das wäre eine Kapazität von zirka 5,6 nF im heute üblichen SI-Einheitensystem. Eine Kapazität von 1 cm im CGS-Einheitensystem entspricht 1,1 pF im SI-Einheitensystem, der Umrechnungsfaktor ist 4 πε₀.

weitere Kennzeichnungen

• Oft wird auch bei Elektrolytkondensatoren ein in mehreren Ziffern verschlüsselter Datumscode aufgedruckt, um das Herstelldatum erkennen zu können, da Elektrolytkondensatoren in Abhängigkeit von der Zeit ihre Kapazität verringern können; zum Beispiel 2313 : 2 = 2002, 3 = März, 13 = 13. Tag, also 13. März 2002. Der Aufbau der Codes kann sich bei verschiedenen Herstellern unterscheiden, da nur wenige sich nach einheitlichen Normen richten. (Siehe auch Kennzeichnung von Elektrolytkondensatoren)
• Sofern es die Bauform des Kondensators zulässt, wird auch der Hersteller, der Betriebstemperaturbereich, die Spannungsfestigkeit und eine Baureihenbezeichnung angebracht, die Aufschluss über den verwendeten Isolator gibt.
• Keramikkondensatoren werden mit ihrer Toleranz und dem gültigen Temperaturbereich gekennzeichnet.
• Die Bezeichnungen X1, X2 sowie Y1 und Y2 dienen der Kennzeichnung von Entstörkondensatoren zur Verwendung in Netzfiltern im Niederspannungsnetz. X-Kondensatoren werden zwischen Außenleiter und Neutralleiter eingesetzt. Der X1-Typ hält einem Spannungsimpuls von 4 kV stand, X2 von 2,5 kV. Durch eine spezielle Konstruktion geraten sie auch bei Überlastung nicht in Brand. Die Y-Typen werden eingesetzt, wenn eine Schutzisolierung überbrückt wird und deren Defekt zu einem Stromschlag führen kann; sie halten Spannungsimpulse der doppelten Höhe stand.

Schaltzeichen

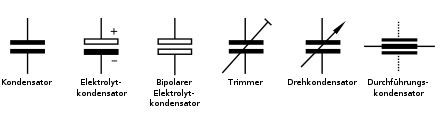
In den unten abgebildeten Schaltzeichen symbolisieren die horizontalen Flächen die separierten Elektroden.

Normung und Ersatzschaltbild

Diskrete Kondensatoren sind Industrieprodukte, die mit etwa 700 Milliarden Stück jährlich hergestellt und eingebaut werden. Wie bei allen Industrieerzeugnissen ist es von entscheidender Bedeutung, dass die elektrischen Werte der Bauelemente präzise erfasst werden um die Reproduzierbarkeit von Schaltfunktionen sicherzustellen. Für Kondensatoren werden die elektrischen Werte und die Kriterien ihrer Messverfahren im internationalen Bereich harmonisiert durch die Rahmenspezifikation IEC 60384-1, die in Deutschland als DIN EN 60384-1 (VDE 0565-1) im Mai 2010 erschienen ist. Diese Norm definiert zunächst die elektrischen Werte eines Kondensators mit Hilfe eines Serien-Ersatzschaltbildes. Darin sind:

Serien-Ersatzschaltbild eines Kondensators

• C, die Kapazität des Kondensators,
• R_isol, der Isolationswiderstand des Dielektrikums bzw. R_Leak, der Widerstand, der den Reststrom bei Elektrolytkondensatoren repräsentiert,
• ESR (engl. Equivalent Series Resistance), der äquivalente Serienwiderstand, in ihm sind die ohmschen Leitungs- und die dielektrischen Umpolungsverluste des Kondensators zusammengefasst
• ESL (engl. Equivalent Series Inductivity L), die Äquivalente Serieninduktivität, sie fasst die parasitäre Induktivität des Bauelementes zusammen.

Mit diesem Ersatzschaltbild, den Vorschriften in der DIN EN 60384-1 und den jeweiligen untergeordneten Bauartspezifikationen können Betriebszustände von Kondensatoren so beschrieben werden, dass für definierte Randbedingungen (Frequenz, Temperatur, anliegende Spannung) reproduzierbare Messergebnisse erzielt werden können.

Elektrotechnische und systemtheoretische Beschreibung

Für die unterschiedlichen Anwendungsbereiche wurde eine Reihe von Beschreibungen entwickelt, die bestimmte Aspekte des Verhaltens eines Kondensators hervorheben.

Feldenergie

Ein geladener Kondensator speichert elektrische Energie in dem elektrischen Feld, das zwischen den geladenen Platten besteht (siehe Berechnung elektrostatischer Felder). Ist ein Kondensator der Kapazität C auf die Spannung U geladen, so enthält sein Feld die Energie E gemäß:

$E = \frac{1}{2}C \cdot U^2$

Zum Laden eines Kondensators werden elektrische Ladungen von der einen Platte zur anderen transportiert. Je weiter der Kondensator während dieses Vorgangs bereits aufgeladen ist, desto stärker ist das bereits zwischen seinen Platten herrschende elektrische Feld E, desto mehr Kraft wird ausgeübt, um die Ladung von einer Platte zur anderen zu bringen. Mit steigender Spannung des Kondensators wird daher zunehmend mehr Arbeit für eine weitere Spannungserhöhung verrichtet. Am Schluss ist die während des Aufladens verrichtete Gesamtarbeit als Feldenergie gespeichert. Beim Entladen wird diese wieder frei.

Ladevorgang

Während des Ladevorgangs eines Kondensators über ein RC-Glied lassen sich Spannungs- sowie Stromverlauf (in der Zeit) durch folgende e-Funktionen beschreiben:

$u_{\mathrm{C}} (t) = U_0 \cdot \biggl(1 - e^{- \frac{t}{\tau}}\biggr) = U_0 \cdot \biggl(1 - e^{- \frac{t}{R_{\mathrm{C}} \cdot C}}\biggr)$ und

$i_{\mathrm{C}} (t) = \frac{U_0}{R_{\mathrm{C}}} \cdot e^{- \frac{t}{\tau}} = I_0 \cdot e^{- \frac{t}{R_{\mathrm{C}} \cdot C}}$

mit u_C als Momentanwert der Spannung am Kondensator, i_C als Momentanwert des Stroms am Kondensator, R_C als ohmscher Widerstand des Kondensators (im Stromkreis), $\tau = R_{\mathrm{C}} \cdot C$ als Zeitkonstante sowie U₀ als Ladespannung und der Zeitkonstante τ. Ein Kondensator erreicht nach einer Ladezeit von τ eine Spannung in Höhe von $0,632 \cdot U_0$; nach einer Ladezeit von nur rund $0,69 \cdot \tau$ hat ein Kondensator bereits 50 % seiner endgültigen beziehungsweise ursprünglichen Spannung erreicht. Er ist nach einer Ladezeit von $t_{\mathrm{C}} \approx 5 \tau$ zu rund 99 % aufgeladen, daher nimmt man in der Praxis an, dass er nach dieser Zeit voll aufgeladen ist.

Entladevorgang

Der Verlauf der elektrischen Spannung und des elektrischen Stroms (in der Zeit) während des Entladevorgangs eines Kondensators lassen sich folgendermaßen als Funktionen darstellen:

$u_{\mathrm{C}} (t) = U_0 \cdot e^{- \frac{t}{\tau}} = U_0 \cdot e^{- \frac{t}{R_{\mathrm{C}} \cdot C}}$ sowie

$i_{\mathrm{C}} (t) = - \frac{U_0}{R_{\mathrm{C}}} \cdot e^{- \frac{t}{\tau}} = - I_0 \cdot e^{- \frac{t}{R_{\mathrm{C}} \cdot C}}$

mit U₀ als Spannung des geladenen Kondensators. An einem Kondensator liegt nach einer Entladezeit von τ nur noch eine Spannung von $0,368 \cdot U_0$ an; nach einer Entladezeit von lediglich näherungsweise $0,69 \cdot \tau$ hat er sich um 50 % entladen. Ein Kondensator ist nach einer Entladezeit von $t_{\mathrm{C}} \approx 5 \tau$ zu rund 99 % entladen, weshalb man in der Praxis annimmt, dass er nach dieser Zeit voll entladen ist (trotzdem sind Restströme/Leckströme zu beachten!).

Zeitbereich

Eine Beziehung zwischen Strom und Spannung ergibt sich durch die zeitliche Ableitung der Elementgleichung des Kondensators Q = CU:

$I = \frac{\mathrm{d}Q}{\mathrm{d}t} = C\frac{\mathrm{d}U}{\mathrm{d}t}$

Das bedeutet, dass der Strom durch den Kondensator proportional der Spannungsänderung am Kondensator ist. Die Aussage, dass der Strom proportional der zeitlichen Ableitung der Spannung ist, lässt sich umkehren: Die Spannung ist proportional zum zeitlichen Integral des Stroms. Legt man beispielsweise einen konstanten Strom an, so folgt daraus eine konstante Spannungsänderung, die Spannung steigt linear an.

Das Aufladen und Entladen eines Kondensators durch eine Spannungsquelle über einen Widerstand resultiert in einen exponentiell abflachenden Spannungsverlauf. Es wird ausführlich unter RC-Glied behandelt.

Phasenverschiebung und Blindwiderstand

Phasenverschiebung zwischen Strom und Spannung an einem Kondensator

Mit einem Komponententester aufgenommene Darstellung der Kennlinie eines Kondensators auf einem Oszilloskop macht die Phasenverschiebung sichtbar

Eine kosinusförmige Wechselspannung mit der Amplitude U_S und der Frequenz f bzw. der Kreisfrequenz ω = 2πf, also

$u(t) = U_\mathrm{S} \cos(\omega t + \varphi_\mathrm{u})\$

an einem Kondensator bewirkt den Stromfluss

$i(t) = C\ \frac{\mathrm{d} u(t)}{\mathrm{d}t} = \omega C U_\mathrm{S} \ (-\sin(\omega t + \varphi_u))$

$i(t) = I_\mathrm{S} (-\sin(\omega t + \varphi_u)) = I_\mathrm{S} \cos(\omega t + \varphi_u + 90^\circ)\,$.

Der Strom fließt zeitlich versetzt zur Spannung („Phasenverschiebung“), er eilt dieser um π/2 bzw. 90° voraus.

$\varphi_i = \varphi_u + \frac{\pi}{2}$

Die Stromstärke I_S ist proportional zur Frequenz f der angelegten Spannung und zur Kapazität C des Kondensators:

I_S∼f

I_S∼C

Das Verhältnis von Spannungsamplitude zu Stromamplitude wird allgemein als Scheinwiderstand bezeichnet; im Falle eines idealen Kondensators, bei dem der Strom der Spannung um genau 90° vorauseilt, als kapazitiver Blindwiderstand X_C:

Phasenverschiebungswinkel:

$\varphi_z = \varphi_u - \varphi_i = - \frac{\pi}{2}$

Blindwiderstand:

$X_\mathrm{C} = \frac{U_\mathrm{S}}{I_\mathrm{S}} \cdot \sin(\varphi_\mathrm{z}) = \frac{U_\mathrm{S}}{\omega C U_\mathrm{S}} \cdot \sin \left(- \frac{\pi}{2}\right)= - \frac{1}{\omega C}\,.$

Die Formel zeigt, dass der elektrische Blindwiderstand des Kondensators mit zunehmender Frequenz bis zum praktischen Kurzschluss bei Hochfrequenz abnimmt und andererseits bei der Frequenz f = 0, also bei Gleichspannung, unendlich groß wird und praktisch wie eine Leitungsunterbrechung wirkt.

Durch die Phasenverschiebung von 90° zwischen Spannung und Strom wird an einem Blindwiderstand im zeitlichen Mittel keine Leistung in Wärme umgewandelt; die Leistung pendelt nur hin und her und wird als Blindleistung bezeichnet.

Wird ein Kondensator von periodischen nichtsinusförmigen Wechselströmen durchflossen, so können diese mittels der Fourieranalyse als eine Summe von sinusförmigen Wechselströmen dargestellt werden. Für diese lässt sich die Verknüpfung von Spannung und Strom am Kondensator auf jede einzelne Sinusschwingung getrennt anwenden, der resultierende nichtsinusförmige Spannungsverlauf am Kondensator ergibt sich dann als Summe der einzelnen sinusförmigen Spannungsverläufe.

Diese Zusammensetzung gilt nur, wenn die Kapazität des Kondensators nicht von der anliegenden Spannung abhängt. In diesem Fall ist der Kondensator ein lineares Bauelement und die damit aufgebauten Schaltungen mit den Methoden der komplexen Wechselstromrechnung zugänglich. Hängt die Kapazität des Kondensators von den Momentanwerten der anliegenden Spannung ab, d. h., die dielektrische Leitfähigkeit des zwischen den Platten befindlichen Dielektrikums ist von der elektrischen Feldstärke abhängig, liegt ein nichtlinearer Kondensator vor. In diesem allgemeinen Fall können die obige Beziehungen zwischen Strom und Spannung am Kondensator nicht angewendet werden.

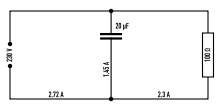
Beispiel für die Kompensation einer Phasenverschiebung

Kapazitive Blindleistung unkompensiert

Blindleistung kompensiert

Die nebenstehende Parallelschaltung aus einem Widerstand und einem Kondensator ist am 230-V-Stromnetz angeschlossen, bei 50 Hz fließen die angegebenen Ströme. Durch den Widerstand fließt 2,3 A Wirkstrom, der bezahlt werden muss, auf den Blindstrom von 1,45 A darf der Elektrizitätszähler nicht reagieren und die Anschlussleitung muss für den Gesamtstrom von 2,72 A bemessen sein (der Strom durch den Kondensator ist um 90° phasenverschoben, daher ist der Gesamtstrom: $\sqrt{2{,}3^2 + 1{,}45^2}\,\mathrm{A} = 2{,}72\,\mathrm{A}$). Einer Wirkleistung von 529 W steht eine Blindleistung von 334 var (W) gegenüber, die zwischen Generator und Kondensator pendelt und Leitungen und Trafos unnötig belastet.

Zur Kompensation dieser Blindleistung wird eine passend gewählte Induktivität von 0,5 H parallel zum Gerät geschaltet, deren Blindstrom ebenfalls 1,45 A beträgt. Die Blindströme von Kondensator und Spule kompensieren sich auf Grund ihrer entgegengesetzten Phasenlagen und die gesamte Stromaufnahme sinkt auf 2,3 A. Die gesamte Anordnung gleicht nun einem gedämpften Schwingkreis.

Impedanz

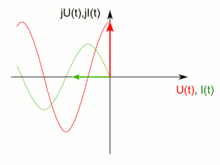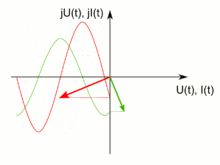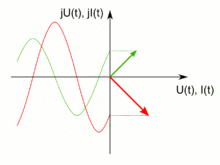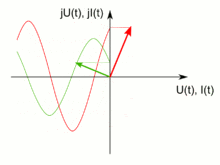
Insbesondere Systeme mit mehreren Kondensatoren, Widerständen und Spulen sind mit dem oben genannten Formalismus umständlich zu beschreiben. Um nicht Phase und Betrag von Signalen getrennt berechnen zu müssen, werden in der komplexen Wechselstromrechnung die Amplituden sinus- und kosinusförmiger Spannungsverläufe in Imaginär- und Realanteil einer komplexen Amplitude der auf die komplexe Ebene erweiterten Kreisfunktion e^jωt zusammengefasst, wobei j die imaginäre Einheit und ω die Kreisfrequenz bezeichnen (die nebenstehende Darstellung verdeutlicht dies). Kleine Buchstaben für Spannungen und Ströme kennzeichnen zeitlich veränderliche Größen; zeitlich konstante Größen werden mit Großbuchstaben gekennzeichnet; komplexe Größen werden unterstrichen:

Darstellung der komplexen Spannung (rot) und des Stromes (grün) am Kondensator

$\underline u(t) = U_0 e^{\mathrm{j}\omega t}\,,$

$\underline i(t) = C \, \frac{\mathrm{d}\underline u(t)}{\mathrm{d}t} = \mathrm{j}\omega C U_0 e^{\mathrm{j}\omega t}\,.$

Der Realteil davon ergibt den Momentanwert der Größe.

Der Zusammenhang zwischen Strom und Spannung, die Impedanz Z_C = R_C + jX_C, lässt sich daraus analog dem ohmschen Widerstand durch Quotientenbildung gewinnen:

$\underline{Z}_\mathrm{C} = \frac{\underline u(t)}{\underline i(t)} = \frac{U_0 e^{\mathrm{j}\omega t}}{\mathrm{j}\omega C U_0 e^{\mathrm{j}\omega t}}=\frac{1}{\mathrm{j}\omega C} = -\mathrm{j}\frac{1}{\omega C}$

Als Beispiel wird der Betrag der Impedanz eines 5-nF-Kondensators bei 3 kHz berechnet:

$Z_\mathrm{C}=\frac{1\,\Omega}{2\pi\cdot3000\cdot5\cdot10^{-9}} = 10{,}6\,\mathrm{k}\Omega$

Man sieht, dass für den (idealen) Kondensator der Wirkwiderstand R_C gleich 0 ist und der Blindwiderstand X_C automatisch das negative Vorzeichen bekommt.

Durch diese Betrachtungsweise werden Differentialgleichungen vermieden. Anstelle der Ableitung tritt eine Multiplikation mit 1/jω = −j/ω (mathematisch negativer Drehsinn).

Da reale Kondensatoren nicht nur eine Kapazität C sondern auch immer noch parasitäre Effekte aufweisen (Serienersatzwiderstand ESR, engl. Equivalent Series Resistance, Serienersatzinduktivität ESL, engl. Equivalent Series Inductance L), ändert sich die Phasenverschiebung zwischen Strom und Spannung. Sie ist nicht mehr 90°, sondern nimmt einen um den Verlustwinkel δ kleineren Wert an. Mit einem Zeigerdiagramm kann auf anschauliche Weise nicht nur die Impedanz $\underline Z$ sondern auch noch der Phasenverschiebungswinkel φ und der ergänzende Verlustwinkel δ dargestellt werden. Dabei ist zu beachten, dass dieses Diagramm jeweils nur für eine Frequenz gilt.

Ersatzschaltbild eines Kondensators bei höherer Frequenz (oben); Darstellung der zugehörigen Impedanz als Zeigerdiagramm in der komplexen Ebene (unten)

Sind die Serienersatzwerte eines Kondensators bekannt, dann kann die Impedanz auch über diese Werte berechnet werden. Er ist dann die Summe der geometrischen (komplexen) Addition der Wirk- und der Blindwiderstände, also des Ersatzserienwiderstandes ESR und des induktiven Blindwiderstandes X_L abzüglich des kapazitiven Blindwiderstandes X_C. Die beiden Blindwiderstände weisen mit der Kreisfrequenz ω folgende Beziehungen auf:

$X_\mathrm{L}=\omega L_{\mathrm{ESL}},\qquad X_\mathrm{C}=-\frac{1}{\omega C}$

Der Scheinwiderstand ist dementsprechend der Betrag der geometrischen (komplexen) Addition der Wirk- und der Blindwiderstände:

$Z=\sqrt{R_{\mathrm{ESR}}^2 + (X_\mathrm{L} + X_\mathrm{C})^2}$

(Zur verwendeten Vorzeichenkonvention siehe Anmerkung unter Blindwiderstand, zur Herleitung siehe unter Komplexe Wechselstromrechnung).

In den Datenblättern der Hersteller von Kondensatoren wird meist der Betrag der Impedanz, also der Scheinwiderstand $|\underline Z|$, angegeben.

Verlustfaktor, Güte und Serienwiderstand

Reale Kondensatoren weisen parasitäre ohmsche Verluste auf. Sie bewirken, dass die Phasenverschiebung zwischen Strom und Spannung an den Klemmen eines realen Kondensators nicht mehr genau 90° beträgt, sondern um den sogenannten Verlustwinkel δ reduziert ist. Dieser Winkel wird als Tangens ausgedrückt und heißt dann Verlustfaktor tan δ (engl.: dissipation factor, abgekürzt DF). Er ergibt sich aus dem Tangens des Phasenwinkels δ zwischen der geometrischen Summe der Blindwiderstände X_C und X_L und dem Ersatzreihenwiderstand ESR. Unter Vernachlässigung der Induktivität ESL sind der Verlustfaktors tan δ, der ESR und die Kapazität C eines Kondensators bei einer bestimmten Frequenz f mit folgender Formel miteinander verbunden:  ^[22]

$\tan \delta = \mathrm{ESR} \cdot \omega C$

Für kleine Werte von δ (ausgedrückt im Bogenmaß) gilt:

$\tan \delta \approx \delta$

Bei verlustarmen Klasse-1-Keramikkondensatoren wird anstelle des Verlustfaktors häufig sein Kehrwert, die Güte Q oder der Gütefaktor spezifiziert.

$Q =\frac{1}{\tan\delta} =\frac{1}{\mathrm{ESR}\cdot \omega C}$

Dieser Wert bezieht sich auf die Bandbreite B bei der Resonanzfrequenz f₀ und berechnet sich nach der Gleichung:

$Q = \frac{f_0}{B} \,$,

wobei sich die Bandbreite, definiert als der Frequenzbereich, an dessen Grenzen sich der Spannungspegel um 3 dB gegenüber dem Mittenwert geändert hat, ergibt aus:

$B = {f_2} - {f_1} \,$.

mit f₂ als obere und f₁ als untere Grenzfrequenz. Da der Verlauf der Impedanzkurve im Resonanzbereich um so steiler ist, je kleiner der ESR ist, kann auch mit der Spezifikation der Güte bzw. des Gütefaktors eine Aussage über die ohmschen Verluste gemacht werden.^[23]

Die oben beschriebene Definition der Spezifikation der ohmschen Verluste in einem Kondensator geht von dem allgemein üblichen und in der Fachgrundspezifikation DIN EN (IEC) 60384-1 spezifizierten Serien-Ersatzschaltbild aus, in dem die dielektrischen und die Leitungsverluste zum ESR bzw. Verlustfaktor zusammengefasst werden. Einige Fachbücher benutzen zur Erklärung des Verlustfaktors aber ein anderes Ersatzschaltbild, in dem die ohmschen Verluste durch einen Widerstand Rp modelliert werden, der (zusätzlich zum Isolationswiderstand) zu einem idealen Kondensator mit der Kapazität C parallelgeschaltet ist. (Wenn in diesen Beschreibungen dann die ohmschen Verluste mit den dielektrischen Verlusten gleichgesetzt werden, dann erfolgt das aus dem Wissen heraus, dass die Leitungsverluste in diesen Kondensatoren vernachlässigbar sind.) Die Verlustleistung P_V ergibt sich damit beim Betrieb des Kondensators an einer Wechselspannung mit dem Effektivwert U zu

$P_\mathrm{v} = \frac{U^2}{R_\mathrm{p}}.$

Der Kehrwert dieses Widerstands ist der Leitwert G (wird auch als Ableitung bezeichnet). Der Tangens des Verlustwinkels δ kann in der Form

$\tan \delta = \frac{I_\mathrm{R}}{I_\mathrm{C}} = \frac{G}{B_\mathrm{C}} = \frac{1}{2\pi f C R_\mathrm{p}}$ ^[24]

dargestellt werden.

Spektralbereich

Eine Beschreibung im Bildbereich der Laplace-Transformation vermeidet die Beschränkung auf harmonische Schwingungen. Für die Impedanz im Bildbereich gilt dann

$Z_\mathrm{C}=\frac{1}{sC}$

Dabei ist s = σ + jω die „komplexe Frequenz“, σ charakterisiert die exponentielle Einhüllende, ω wiederum die Kreisfrequenz.

Parallel- und Reihenschaltung

Parallelschaltung von Kondensatoren

Kondensatoren sind in einer elektrischen Schaltung als Parallelschaltung miteinander verbunden, wenn dieselbe Spannung an allen Bauteilen anliegt. In diesem Fall addieren sich die Kapazitäten der einzelnen Bauteile zur Gesamtkapazität:

$C_{\rm ges} = C_1 + C_2 + \cdots + C_n \,\!$

Durch die Parallelschaltung erhöht sich sowohl die Gesamtkapazität als auch die Strombelastbarkeit der Schaltung. Der gesamte Stromfluss I_ges verteilt sich auf den k-ten Kondensator gemäß:

$I_k=\frac{C_k}{C_{\rm ges}}\cdot I_{\rm ges}$

Neben einer Erhöhung der Kapazität und Strombelastbarkeit der Schaltung, reduzieren sich durch parallel geschaltete Kondensatoren auch deren unerwünschte parasitäre Eigenschaften wie Induktivität (ESL) und Ersatzserienwiderstand (ESR).

Reihenschaltung von Kondensatoren

Eine Reihenschaltung liegt vor, wenn durch zwei oder mehr Kondensatoren derselbe elektrische Strom fließt. Dann addiert sich der Kehrwert der Kapazität der einzelnen Bauteile zum Kehrwert der Gesamtkapazität:

$\frac{1}{C_\mathrm{ges}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n}$

Die Reihenschaltung wird beispielsweise angewendet, um eine hohe Spannung auf mehrere Kondensatoren mit geringerer Spannungsfestigkeit zu verteilen, wenn kein Einzelbauelement für diese Spannung verfügbar ist. Da die Isolationswiderstände bzw. bei Elektrolytkondensatoren die Restströme der einzelnen Kondensatoren stark unterschiedlich sein können, kann über unterschiedliche Isolationswiderstände bzw. Restströme eine Spannungsaufteilung entstehen, die nicht mit der kapazitiven Spannungsaufteilung übereinstimmt. Dadurch können unter Umständen einzelne Kondensatoren mit einer zu hohen Spannung beaufschlagt werden, was zu Kurzschlüssen führen könnte. Aus diesem Grunde werden in der Regel in Reihe geschaltete Kondensatoren symmetriert, das heißt, jedem Kondensator wird ein definierter hochohmiger Widerstand (jedoch deutlich geringer als R_Leak) parallel geschaltet, damit eine definierte Spannungsaufteilung entsteht.

Material- und bauartbedingte Merkmale

Kapazität und Spannungsfestigkeit

Die überwiegende Anzahl der industriell hergestellten Kondensatoren sind im weitesten Sinne als Plattenkondensatoren ausgeführt. Die Kapazität ergibt sich damit aus der Oberfläche der Elektroden, der Dielektrizitätszahl des verwendeten Dielektrikums und dem Kehrwert des Abstandes der Elektroden zueinander. Neben diesen drei Parametern, die bei realen Kondensatoren erheblich voneinander abweichen können, spielt die Verarbeitbarkeit der Materialien eine entscheidende Rolle. Dünne, mechanisch flexible Folien lassen sich gewickelt oder gestapelt leicht zu großen Bauformen mit hohen Kapazitätswerten verarbeiten. Hauchdünne metallisierte Keramikschichten zu SMD-Bauformen gesintert bieten dagegen beste Voraussetzungen für die Miniaturisierung von Schaltungen.

Materialdaten der wichtigsten in der Elektronik verwendeten Kondensatorfamilien

Kondensatorfamilie	Dielektrikum	Dielektrizitätszahl bei 1 kHz	Spannungsfestigkeit in V/µm	Minimale Dicke des Dielektrikums in µm
Keramikkondensator, Klasse 1	paraelektrisch	20…40	< 100(?)	1
Keramikkondensator, Klasse 2	ferroelektrisch	200…14000	< 25(?)	1
Kunststoff-Folienkondensator	PET	3,3	580	0,7
Kunststoff-Folienkondensator	PEN	3,0	500 (?)	0,9
Kunststoff-Folienkondensator	PPS	3,0	470	1,2
Kunststoff-Folienkondensator	PP	2,2	650	3,0
Aluminium-Elektrolytkondensator	Al2O3	8,4…9,6[25]	700	0,01
Tantal-Elektrolytkondensator	Ta2O5	24…28[25]	625	0,01

Kapazitäts- und Spannungsbereiche verschiedener Kondensator-Technologien

Reale Kondensatoren können nicht bis zu einer beliebigen Spannung aufgeladen werden. Überschreitet man die zulässige Spannung, die durch die Spannungsfestigkeit des jeweiligen Dielektrikums bestimmt wird, bis zur „Durchschlagsspannung“, so schlägt der Kondensator durch, das heißt, es fließt plötzlich ein erheblich größerer Strom über eine Funkenstrecke oder auf eine ähnliche Art ab. Meist führt das zur Zerstörung des Kondensators (zum Beispiel Kurzschluss oder gar eine Explosion) und zu weitergehenden Zerstörungen an den Geräten. Die zulässige Höchstspannung ist abhängig von der Einwirkzeit, der Temperatur, der elektrischen Belastung und bei Wechselspannungsanwendungen auch von der Frequenz.

Bei Keramikkondensatoren ist es nicht möglich, eine physikalisch begründete präzise Durchschlagsspannung einer keramischen Schicht für eine definierte Dicke festzulegen. Die Durchschlagsspannung kann in Abhängigkeit von der Zusammensetzung des Elektrodenmaterials und der Sinterbedingungen bis um den Faktor 10 variieren.

Metallisierte Kunststoff-Folienkondensatoren besitzen die Fähigkeit zur Selbstheilung, ein Durchschlag führt dabei lediglich zur lokalen Verdampfung der dünnen Elektroden. Der Kondensator verliert jedoch einen bestimmten, geringen Teil seiner Kapazität ohne dass seine Funktionsfähigkeit darunter leidet.

Elektrolytkondensatoren sind vom Aufbau her gepolte Bauelemente. Die Spannungsfestigkeit der Oxidschichten gilt nur bei richtig gepolt anliegender Spannung. Falschpolspannung zerstört den Elektrolytkondensator.

Frequenzabhängigkeit

Die Frequenzabhängigkeit der Kapazität und des Verlustfaktors von Kondensatoren ergibt sich aus zwei Komponenten:

• aus dem frequenzabhängigen Verhalten des Dielektrikums von Kondensatoren (ausgenommen Klasse-1-Keramikkondensatoren). Das beeinflusst den Kapazitätswert, der mit steigender Frequenz abnimmt und die Verluste im Dielektrikum, die mit steigender Frequenz zunehmen.
• eine bauartbedingte, parasitäre Induktivität (Anschlüsse, Aufbau), die im Ersatzschaltbild als eine in Reihe liegende Induktivität dargestellt wird. Sie wird ESL (von engl. equivalent series inductance) genannt und führt zu einer charakteristischen Eigenresonanzfrequenz, bei der der Kondensator seine minimale Impedanz besitzt.

Ist bei einer Anwendung eine geringe Impedanz in einem weiten Frequenzbereich erforderlich, schaltet man Kondensatoren verschiedener Bauarten parallel. Bekannt ist das Parallelschalten eines Elektrolytkondensators mit einem Keramikkondensator oder auch das Parallelschalten von Keramikkondensatoren verschiedener Baugrößen.

Temperaturabhängigkeit

Die Kapazität eines Kondensators ist temperaturabhängig, wobei die verschiedenen Dielektrika starke Unterschiede im Verhalten bewirken. Für Keramikkondensatoren gibt es paraelektrische Dielektrika mit positivem, negativem und nahe null betragendem Temperaturkoeffizienten. Auch einige Kunststoff-Folienkondensatoren weisen ähnliche Eigenschaften auf. Bei hohen Stabilitätsanforderungen an zum Beispiel Schwingkreisen können auf diese Weise Temperatureinflüsse anderer Bauteile ausgeglichen werden. Keramikkondensatoren aus ferroelektrischer Keramik sowie Elektrolytkondensatoren haben günstigerweise eine sehr hohe Permittivität, was zu einem hohen Kapazitätswert führt, haben jedoch auch einen hohen, meist nichtlinearen Temperaturkoeffizienten und eignen sich daher für Anwendungen ohne große Anforderungen an die Stabilität wie zum Beispiel Siebung, Funkentstörung, Kopplung oder Entkopplung.

Temperaturabhängigkeit der Kapazität häufig eingesetzter Kondensatoren

Kondensatorfamilie, dielektrisches Material	Bezeichnung	ΔC/C	Üblicher Temperaturbereich
Keramikkondensator Klasse 1, paraelektrisch	NP0	±0,3 % bzw. ± 30 ppm/K	−55…+125 °C
Keramikkondensator Klasse 2, ferroelektrisch	X7R	±15 %	−55…+125 °C
Keramikkondensator Klasse 2, ferroelektrisch	Y5V	+22 % / −82 %	−30…+85 °C
Folienkondensator, Polyphenylensulfid (PPS)	(F)KI, MKI	±1,5 %	−40…+150 °C
Folienkondensator, Polypropylen (PP)	(F)KP, MKP	±2,5 %	−40…+105 °C
Folienkondensator, Polyethylennaphthalat (PEN)	(F)KN, MKN	±5 %	−40…+150 °C
Folienkondensator, Polyester (PET)	(F)KT, MKT	+5 %	−40…+125/150 °C
metallisiertes Papier (Ölgetränkt)	MP	±10 %	−25…+85 °C
Aluminium-Elektrolytkondensator, Al2O3		±20 %	−40…+85/105/125 °C
Tantal-Elektrolytkondensator, Ta2O3		±20 %	−40…+125 °C

Spannungsabhängigkeit

Ferroelektrische Klasse-2-Keramikkondensatoren zeigen einen spannungsabhängigen, nichtlinearen Verlauf der Kapazität. Daraus resultiert zum Beispiel bei Anwendungen im Audiobereich ein Klirrfaktor. Dort werden bei hohen Qualitätsanforderungen deshalb oft Folienkondensatoren eingesetzt.

Formal lässt sich ein nichtlinearer Kondensator durch eine von der Momentanspannung u abhängige Dielektrizitätszahl ε_r(u) beschreiben. Diese relative Dielektrizitätszahl ist also nicht konstant, sondern ist als Funktion der am Kondensator anliegenden Spannung u zu betrachten. Beispielsweise ist bei einem nichtlinearen Kondensator die spannungsabhängige Kapazität gegeben als:

$C(u) = \varepsilon_r(u) \cdot \varepsilon_0 \cdot \frac{A}{d}$

Die Funktion ε_r(u) ist werkstoffabhängig.

Klasse-2-Keramikkondensatoren weisen, abhängig von der Art der Keramik, bei Nennspannung einen Abfall der Kapazität von bis zu 90 % gegenüber der genormten Messspannung von 0,5 oder 1 V auf.

Alterung

Die elektrischen Eigenschaften einiger Kondensatorfamilien sind Alterungsprozessen unterworfen, sie sind zeitabhängig.

Keramische Klasse-2-Kondensatoren mit Dielektrika aus ferroelektrischen Materialien zeigen eine ferroelektrische Curietemperatur. Oberhalb von etwa 120 °C, der Curietemperatur von Bariumtitanat, ist die Keramik nicht mehr ferroelektrisch. Da diese Temperatur beim Löten von SMD-Kondensatoren deutlich überschritten wird, werden die dielektrischen Gebiete parallel ausgerichteter dielektrischer Dipole erst beim Abkühlen des Materials neu gebildet. Diese Bereiche zerfallen aufgrund mangelnder Stabilität der Domänen jedoch im Laufe der Zeit, die Dielektrizitätszahl verringert sich und damit sinkt die Kapazität des Kondensators, der Kondensator altert. Die Alterung folgt einem logarithmischem Gesetz. Dieses definiert die Alterungskonstante als Kapazitätsabnahme in Prozent während einer Zeitdekade, zum Beispiel in der Zeit von 1 h auf 10 h.^[26]

Aluminium-Elektrolytkondensatoren mit flüssigem Elektrolyten altern infolge der langsamen, temperaturabhängigen Austrocknung des Elektrolyten im Laufe der Zeit. Dabei verändert sich zunächst die Leitfähigkeit des Elektrolyten, die ohmschen Verluste (ESR) des Kondensators steigen an. Später sinkt dann auch der Benetzungsgrad der porigen Anodenstrukturen wodurch die Kapazität absinkt. Sofern keine anderen chemischen Prozesse im Kondensator auftreten, kann die Alterung von „Elkos“ mit dem sog. „10-Grad-Gesetz“ beschrieben werden. Die Lebensdauer dieser Kondensatoren halbiert sich, wenn die auf den Kondensator einwirkende Temperatur um 10 °C ansteigt.

Auch Doppelschichtkondensatoren sind einem Alterungsprozess durch Verdunstung des Elektrolyten unterworfen. Die damit verbundene Erhöhung des ESR begrenzt die mögliche Anzahl von Ladezyklen des Kondensators.

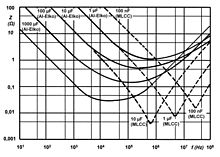
Scheinwiderstand und Resonanz

Typische Impedanzverläufe des Scheinwiderstandes $|\underline Z|$ verschiedener Kondensatoren mit unterschiedlicher Kapazität. Je kleiner die Kapazität ist, desto höher wird die Frequenz, die der Kondensator ableiten (filtern, sieben) kann.

Die Anwendungsbereiche von Kondensatoren nutzen überwiegend die Eigenschaft als kapazitiver Wechselstromwiderstand zum Filtern, Sieben, Koppeln und Entkoppeln von erwünschten oder unerwünschten Frequenzen oder zum Erzeugen von Frequenzen in Schwingkreisen. Aus diesem Grunde ist das Frequenzverhalten der Impedanz ein mitentscheidender Faktor für den Einsatz in einer Schaltungsfunktion.

Der Betrag der Impedanz, der Scheinwiderstand $|\underline Z|$, wird in Datenblättern von Kondensatoren häufig als Kurve über der Frequenz f dargestellt. Dabei sinkt mit steigender Frequenz zunächst der Scheinwiderstand ab bis zu einem Wendepunkt in der Kurve, ab dem er wieder ansteigt. Dieser Verlauf ist das Resultat der Konstruktion realer Kondensatoren, die nicht nur eine Kapazität C sondern immer auch noch eine in Serie dazu liegende parasitäre Induktivität L (ESL) aufweisen. (Siehe Absatz „Normung und Ersatzschaltbild“). Kapazität C und Induktivität ESL bilden einen Serienschwingkreis ^[27],  ^[28], der bei der Frequenz

$f_0 = \frac{1}{2 \pi \sqrt{L C}}$

in Resonanz gerät. An diesem Punkt hat der Scheinwiderstand nur noch einen Realanteil, den ESR des Kondensators. Darüber hinaus überwiegt der induktive Anteil, und der Kondensator ist als solcher unwirksam, da er dann wie eine Spule wirkt.

Herkömmliche Aluminium-Elektrolytkondensatoren haben aufgrund ihrer großen Kapazität relativ gute Siebeigenschaften im Bereich niedriger Frequenzen bis etwa 1 MHz. Sie weisen aber aufgrund ihres gewickelten Aufbaus eine relativ hohe Induktivität auf, so dass sie für den Einsatz bei höheren Frequenzen ungeeignet sind. Keramik- und Folienkondensatoren sind schon von ihren kleineren Kapazitäten her für höhere Frequenzen bis zu einigen 100 MHz geeignet, Sie haben außerdem durch ihre Konstruktion (Stirnkontaktierung der Folien, Parallelschaltung der Elektroden) deutlich niedrigere parasitäre Induktivitätswerte. Um einen sehr breiten Frequenzbereich abdecken zu können, wird häufig ein Elektrolytkondensator mit einem Keramik- oder Folienkondensator parallel geschaltet.

Viele Neuentwicklungen bei Kondensatoren haben unter anderem eine Verringerung der parasitären Induktivität ESL zum Ziel, um durch Erhöhung der Resonanzfrequenz zum Beispiel die Schaltgeschwindigkeit digitaler Schaltungen erhöhen zu können. Durch die Miniaturisierung speziell bei den SMD-Keramikvielschicht-Chipkondensatoren (MLCC) wurde hier schon viel erreicht. Eine weitere Verringerung der parasitären Induktivität ist durch Kontaktierung der Elektroden an der Längsseite anstatt der Querseite erreicht worden. Die „Face down“ Konstruktion verbunden mit der Multi-Anodentechnik hat bei Tantal-Elektrolytkondensatoren ebenfalls zu einer Verringerung der ESL geführt. Aber auch neue Kondensatorfamilien wie die sog. MOS- oder Silizium-Kondensatoren bieten Lösungen an, wenn Kondensatoren für sehr hohe Frequenzen bis in den GHz-Bereich benötigt werden.

Ohmsche Verluste

Ohmsche Verluste in diskreten, handelsüblichen Kondensatoren für die Elektronik entstehen durch dielektrische Umpolarisierungsverluste im Wechselfeld und durch den ohmschen Widerstand der Zuleitungen und der Elektroden des Kondensators. Bei Aluminium-Elektrolytkondensatoren trägt besonders die begrenzte Leitfähigkeit flüssiger Elektrolyte zu diesen Verlusten bei. Die verschiedenen Verlustwiderstände werden, da sie bei industriell gefertigten Kondensatoren messtechnisch nicht voneinander getrennt gemessen werden können, zu einem gemeinsamen Wert zusammengefasst. Sie können in den jeweiligen Datenblättern als Verlustfaktor tan δ, als Güte Q und als Ersatzreihenwiderstand ESR dargestellt werden Der Zahlenwert des Verlustfaktors und der Güte ist, bei gleicher Messfrequenz, innerhalb eines spezifizierten Bereiches unabhängig von dem Kapazitätswert des Kondensators. Der ESR dagegen ist unabhängig von den Blindwiderständen und ist eine Größe, die jeden Kondensator einzeln kennzeichnet. Über ihn kann mit Hilfe der Gleichung

$P =\ I^2 \cdot\, \mathrm{ESR}$

leicht die im Kondensator entstehende Verlustwärme P bei Strombelastung mit dem Strom I errechnet werden.

Bei Leistungskondensatoren wie z. B. Vakuumkondensatoren, große Keramik- und Polypropylen-Folienkondensatoren werden die ohmschen Verluste anders definiert. Anstatt Verlustfaktor, Güte oder ESR wird hier oft die maximale Strom- oder Impulsbelastung spezifiziert. Auch diese Angabe ist letztendlich ein Ausdruck der ohmschen Verluste des Kondensators und ermittelt sich aus der zulässigen Verlustwärme, die über die ohmschen Verluste bei der Strombelastung entsteht.

Die ohmschen Verluste von Kondensatoren hängen von der Bauart ab, sind also spezifisch für eine bestimmte Fertigungstechnik. Innerhalb einer Bauart sinken die ohmschen Verluste mit steigender Kapazität. Dies scheint zunächst paradox, weil mit steigender Kapazität die dielektrischen Verluste größer werden müssten. Das dies nicht der Fall ist liegt am technischen Aufbau der Kondensatorarten. Anschaulich wird es am Beispiel der Keramik-Vielschichtkondensatoren. Die vielen Einzelkondensatoren im Schichtverbund sind parallel geschaltet, so dass auch ihre einzelnen Verlustwiderstände parallel geschaltet sind. Dadurch reduziert sich der Gesamtwiderstand entsprechend der Anzahl parallel geschalteter Einzelkondensatoren. Bei Folienkondensatoren bewirkt die Stirnflächenkontaktierung des Wickels ähnliches. Die Art der Kontaktierung kann als eine Vielzahl parallel geschalteter Einzelkondensatoren beschrieben werden. Bei Elektrolytkondensatoren, bei denen die Zuleitungsverluste über den Elektrolyten die ohmschen Verluste maßgeblich bestimmen, kann bei größer werdenden Elektrodenflächen die steigende Anzahl der Zuleitungspfade als Parallelschaltung vieler Einzelwiderstände verstanden werden, wodurch sich die gesamten ohmschen Verluste verringern. Bei sehr großen Aluminium-Elektrolytkondensatoren reduziert außerdem häufig eine Mehrfachkontaktierung der Anoden- und Kathodenfolien die ohmschen Verluste. Aus demselben Grund werden Tantal-Elektrolytkondensatoren in einigen Ausführungsformen mit Mehrfach-Anoden gefertigt.

Die ohmschen Verluste sind Wechselstromverluste, Gleichstromverluste (Isolationswiderstand, Reststrom) bei Kondensatoren sind meist vernachlässigbar. Die Messfrequenz zum Messen der Verluste muss eindeutig festgelegt sein. Da aber handelsübliche Kondensatoren mit Kapazitätswerten von pF (Pikofarad, 10⁻¹² F) bis einigen 100 F bei Doppelschichtkondensatoren mit etwa 14 Zehnerpotenzen einen außerordentlich großen Kapazitätsbereich abdecken, ist es nicht möglich, mit nur einer Messfrequenz den gesamten Bereich zu erfassen. Nach der Fachgrundspezifikation für Kondensatoren, der DIN EN (IEC) 60384-1, sollen die ohmschen Verluste mit derselben Frequenz gemessen werden, die auch zur Messung der Kapazität verwendet wird, mit:

• 100 (120) Hz für Elektrolytkondensatoren und andere Kondensatoren mit C > 10 µF
• 1 kHz (Bezugsfrequenz) oder 10 kHz für andere Kondensatoren mit 1 nF ≤ C ≤ 10 µF
• 100 kHz, 1 MHz (Bezugsfrequenz) oder 10 MHz für andere Kondensatoren mit C ≤ 1 nF

Die ohmschen Verluste von Kondensatoren sind frequenz-, temperatur- und zum Teil auch zeitabhängig (Alterung). Eine Umrechnung der Einheit tan δ in ESR und umgekehrt ist möglich, erfordert aber einige Erfahrung. Sie kann nur erfolgen, wenn die Messfrequenz hinreichend weit entfernt von der Resonanzfrequenz ist. Denn bei der Resonanz ändert sich der Kondensator von einem kapazitiven in ein induktives Bauelement, dabei ändert sich der Verlustwinkel dramatisch und ist deshalb zur Umrechnung nicht mehr geeignet.

Ohmsche Verluste unterschiedlicher Klasse-1-Kondensatorarten

Die Güte und der Verlustfaktor sind charakteristische Größen der ohmschen Verluste im Dielektrikum bestimmter Kondensatoren, bei denen die Leitungsverluste vernachlässigbar sind. Diese Kondensatoren, bei den Keramikkondensatoren „Klasse-1“ genannt, werden überwiegend in Frequenz bestimmenden Schaltungen oder in Hochleistungsanwendungen als Leistungskondensatoren eingesetzt. Als Messfrequenz für den in der Elektronik üblichen Kapazitätsbereich von 30 pF bis 1 nF wird von großen Herstellern meist 1 MHz genommen. Mit dieser hohen Frequenz wird auch Bezug auf die Anwendung solcher Kondensatoren genommen, die überwiegend im höheren Frequenzbereich liegt. Die betroffenen kleinen Kapazitätswerte mit den dazu vorhandenen niedrigen ESL-Werten stellen außerdem sicher, dass der Messwert noch weit genug von der Resonanzfrequenz entfernt ist.

Die folgende Tabelle, in der die ESR-Werte rechnerisch ermittelt wurden, gibt einen Überblick über die ohmschen Verluste (Maximalwerte) unterschiedlicher Kondensatorarten (ohne Leistungskondensatoren) bei 1 MHz in für Frequenz bestimmende Anwendungen in der Elektronik:

Ohmsche Verluste unterschiedlicher Kondensatorarten
für frequenzbestimmende Schaltungen (Bezugsfrequenz 1 MHz)

Kondensatorart	Kapazität in pF	ESR 100 pF in mΩ	ESR 1000 pF in mΩ	tan δ in 10−4	Güte Q
Siliziumkondensator [29]	560	400	—	2,5	4000
Glimmerkondensator [30]	1000	650	65	4	2500
Klasse-1-Keramikkondensator (NP0) [31]	1000	1600	160	10	1000

Ohmsche Verluste unterschiedlicher Kondensatorarten im mittleren Kapazitätsbereich

Der Kapazitätsbereich von 1 nF bis 10 µF wird überwiegend von Klasse-1- und Klasse-2-Keramikkondensatoren und von Kunststoff-Folienkondensatoren abgedeckt. Elektrolytkondensatoren werden in diesem Kapazitätsbereich weniger häufig eingesetzt. Dieser Kapazitätsbereich ist durch eine Vielzahl unterschiedlicher Anwendungen mit stark unterschiedlichen Anforderungen gekennzeichnet. Die ohmschen Verluste dieser Kondensatoren in den Datenblättern der Hersteller werden überwiegend über den Verlustfaktor spezifiziert. Allerdings sind in diesem Bereich auch Wechselspannungs- und Impulskondensatoren angesiedelt, die sich über eine Strombelastung spezifizieren.

In der folgenden Tabelle sind als allgemeines Beispiel die Verlustfaktoren (Maximalwerte) bei 1 kHz, 10 kHz und 100 kHz sowie die daraus abgeleiteten ESR-Werte für einen 100 nF Kapazitätswert gelistet.

Ohmsche Verluste unterschiedlicher Kondensatorarten
mit 1 nF < C ≤ 10 µF (Bezugswert 100 nF)

Kondensatorart	ESR 1 kHz in mΩ	ESR 10 kHz in mΩ	ESR 100 kHz in mΩ	tan δ in 10−3	tan δ in 10−3	tan δ in 10−3
Klasse-1- Keramikkondensator (NP0, N750) [32]	1600	160	16	1	1	1
Klasse-2- Keramikkondensator (X7R, Y5V) [33]	4000	400	40	2,5	2,5	2,5
PP-Folienkondensator (Polypropylen) [34]	6400	800	160	4	5	10
PET-Folienkondensator (Polyester)	12700	2400	480	8	15	30
PEN-Folienkondensator (Polyethylennaphthalat)	12700	2400	480	8	15	30
PPS-Folienkondensator (Polyphenylensulfid)	24000	3200	800	15	20	50

Ohmsche Verluste unterschiedlicher Kondensatorarten im höheren Kapazitätsbereich

Kondensatoren mit Kapazitätswerten größer 10 µF werden überwiegend in Anwendungen im Bereich der Stromversorgungen, der Sieb- und der Stützschaltungen eingesetzt. Es ist der typische Kapazitätsbereich, in dem Elektrolytkondensatoren und hochkapazitive Keramik-Vielschichtkondensatoren eingesetzt werden. Nach der Fachgrundspezifikation für Kondensatoren, der DIN EN (IEC) 60384-1 sollen die ohmschen Verluste solcher Kondensatoren mit 100 Hz (bzw. 120 Hz) gemessen werden. Da in der Elektronik die Arbeitsfrequenzen in den letzten Jahrzehnten aber deutlich gestiegen sind und auch im Bereich der Schaltnetzteile mit sehr viel höheren Frequenzen gearbeitet wird, finden sich in den Datenblättern, speziell denen von Elektrolytkondensatoren, auch häufig die 100-kHz-ESR-Werte.

Die folgende Tabelle gibt einen Überblick über die ohmschen Verluste (Maximalwerte) verschiedener Kondensatorarten für Sieb- oder Stützanwendungen im Niedervoltbereich. Zur Vergleichbarkeit der Kondensatorarten miteinander ist jeweils die Kapazität von etwa 100 µF und eine Spannungsfestigkeit von 10 bis 16 V gewählt worden. Da für diesen Anwendungsbereich in der Elektronik das Bauvolumen eine große Rolle spielt, sind in der Tabelle die Abmessungen mit aufgeführt worden. Die Zeile mit der Kapazität 2200 µF ist als Beispiel dafür aufgeführt, dass mit größerer Kapazität und Baugröße auch bei der preiswertesten Kondensatorart, den „Elkos“, niedrige ESR-Werte zu erreichen sind. Im Übrigen ist der höhere ESR bei den „Elkos“ mitunter schaltungstechnisch sogar erwünscht, weil die Dämpfung über diese Verluste unerwünschte Resonanzen auf Leiterplatten verhindern kann.

Ohmsche Verluste unterschiedlicher Kondensatorarten
für Sieb- und Stützanwendungen im Niedervoltbereich

Kondensatorart	Kap./Spg in µF/V	L×B×H in mm³ bzw. D×L in mm²	ESR 100 Hz in mΩ)	tan δ 100 Hz in %	ESR 100 kHz in mΩ
Klasse-2-Keramikkondensator (X5R) [35]	100/6,3	3,2×1,6×1,6	2400	15	typ. 2
Klasse-2-Keramikkondensator (YV5)	100/6,3	3,2×1,6×1,6	3180	20	—
Tantal-Elektrolytkondensator mit Polymer-Elektrolyten [36]	100/10	7,3×4,3×2,8	1600	10	18
Tantal-Elektrolytkondensator mit Braunstein-Elektrolyten	100/10	7,3×4,3×2,8	1275	8	150
Aluminium-Elektrolytkondensator mit Polymer-Elektrolyten	100/10	7,3×4,3×1,6	960	6	15
Aluminium-Elektrolytkondensator mit TCNQ-Elektrolyten [37]	120/10	8×6,9×8,3	1600	12	35
Aluminium-Elektrolytkondensator mit flüssigem Elektrolyten [38]	150/10	6,3×5,8	2020	19	260
Aluminium-Elektrolytkondensator mit flüssigem Elektrolyten [39]	2200/10	12,5×20	130	18	90

Wechselstrombelastbarkeit

Geplatzte Elektrolytkondensatoren, die an dem geöffnetem Sollbruchventil erkennbar sind. Verursacht vermutlich durch überhöhte Wechselstrombelastung über die Kondensatoren im Schaltregler eines PC-Mainboards.

Dieser defekte Kondensator in einem Nähmaschinenpedal entwickelte nicht nur starke Wärme, sondern sorgte auch für selbstständiges Anlaufen des Maschinenmotors

Eine Wechselspannung oder eine einer Gleichspannung überlagerte Wechselspannung bewirkt Lade- und Entladevorgänge in einem Kondensator. Es fließt ein Wechselstrom, der Umgangssprachlich auch Rippelstrom genannt wird. Der Effektivwert dieses Wechselstromes bewirkt über die ohmschen Verluste des Kondensators (ESR, Verlustfaktor) eine Verlustleistung P_V, die das Bauelement von innen heraus erwärmt.

$P_\mathrm{V} = I^2 \cdot \,\mathrm{ESR}$

oder

$P_\mathrm{v} = 2\pi f \cdot C \cdot U^2 \cdot \tan \delta \,$

Die entstandene Wärme wird über Konvektion und Wärmeleitung an die Umwelt abgegeben. Die Menge der Wärme, die an die Umwelt abgegeben werden kann, hängt von den Maßen des Kondensators und den Bedingungen auf der Leiterplatte und der Umgebung ab.

Die zulässige Wechselstrombelastung von Elektrolytkondensatoren und Kunststoff-Folienkondensatoren wird allgemein so berechnet, dass maximal eine zulässige interne Temperaturerhöhung von 3 bis 10 K entsteht. Bei Keramikkondensatoren kann die Wechselstrombelastung so spezifiziert werden, dass bei einer gegebenen Umgebungstemperatur durch die im Kondensator entstehende Wärme die spezifizierte Maximaltemperatur nicht überschritten wird.

In den Datenblättern von Folienkondensatoren und Keramikkondensatoren wird anstelle eines Wechselstromes oft eine maximal zulässige effektive Wechselspannung spezifiziert, die innerhalb des Nenntemperaturbereiches am Kondensator dauernd anliegen darf. Da mit steigender Frequenz die ohmschen Verluste im Kondensator ansteigen, die interne Wärmeentwicklung bei gleichbleibender Effektivspannung also größer wird, muss bei höheren Frequenzen die Spannung reduziert werden, um die zulässige Temperaturerhöhung einzuhalten.

Besonders bei Elektrolytkondensatoren ist eine hohe Wechselstrombelastung kritisch. Da sich der Kondensator erwärmt, wird die zu erwartende Lebensdauer reduziert. Wird durch überhöhte Wechselstrombelastung die maximal zulässige Temperatur überschritten, so kann der flüssige Elektrolyt unter Umständen in den Siedebereich kommen und den Kondensator so zum Platzen bringen.

Isolationswiderstand und Selbstentladung

Ein auf eine Gleichspannung U₀ aufgeladener realer Kondensator entlädt sich mit der Zeit von selbst. Dieser Effekt kann durch einen endlichen Isolationswiderstand R_Isol des Dielektrikums beschrieben werden, der zu einem idealen Kondensator mit der Kapazität C parallel geschaltet ist ^[40]. Der fließende Strom wird als Leckstrom bezeichnet; er wird bei Baureihen häufig als Funktion der Kapazität spezifiziert. Der zeitliche Verlauf der absinkenden Kondensatorspannung hat die Form

$u(t) = U_0 \cdot \mathrm{e}^{-t/\tau_\mathrm{s}},$

wobei

$\tau_\mathrm{s} = R_\mathrm{is} \cdot C$

die Selbstentladezeitkonstante ist. Nach der Zeit $\tau_\mathrm{s}\,$ ist die Kondensatorspannung U₀ auf 37 % des Anfangswertes abgesunken. Die Selbstentladezeitkonstante ist ein Maß für die Isolation des Dielektrikums zwischen den Elektroden eines Kondensators. Diese Zeitkonstante ist beispielsweise wichtig, wenn ein Kondensator als zeitbestimmendes Glied (zum Beispiel in Zeitrelais) oder zur Speicherung eines Spannungswertes wie in einer Abtast-Halte-Schaltung oder Integrierern eingesetzt wird.

Keramikkondensatoren der Klasse-1 müssen gemäß geltender Normen einen Isolationswiderstand von mindestens 10 GΩ, die der Klasse mindestens 4 GΩ oder eine Selbstentladezeitkonstante von mindestens 100 s besitzen. Der typische Wert liegt meist darüber. Kunststoff-Folienkondensatoren haben typischerweise einen Isolationswiderstand zwischen 6 und 12 GΩ . Das entspricht für Kondensatoren im µF-Bereich einer Selbstentladezeitkonstante von 2000 bis 4000 s^[41].

Bei Elektrolytkondensatoren wird der Isolationswiderstand des Oxidschichtdielektrikums über den Reststrom des Kondensators definiert.

Der Isolationswiderstand bzw. die Selbstentladezeitkonstante ist teilweise stark temperaturabhängig und sinkt mit steigender Temperatur. Der Isolationswiderstand bzw. die Selbstentladezeitkonstante darf nicht verwechselt werden mit der Isolierung des Bauelementes gegenüber der Umgebung.

Reststrom, Leckstrom

Bei Elektrolytkondensatoren wird nicht der Isolationswiderstand definiert, sondern der Reststrom, auch „Leckstrom“, (engl. Leakage Current), genannt.

Der Reststrom eines Elektrolytkondensators ist der Gleichstrom, der durch den Kondensator fließt, wenn eine Gleichspannung an die Anschlüssen des Kondensators gelegt wird. Er entsteht aus einer Schwächung der Oxidschicht durch chemische Prozesse während Lagerzeiten und durch Strombrücken außerhalb der Kondensatorzelle. Der Reststrom ist kapazitäts-, spannungs-, zeit- und temperaturabhängig. Er ist außerdem noch abhängig von der Vorgeschichte, zum Beispiel von der Temperaturbelastung durch einen Lötprozess.

Bedingt durch Selbstheilungseffekte in Elektrolytkondensatoren wird der Reststrom normalerweise immer geringer, je länger der Kondensator an Spannung liegt. Obwohl die Größenordnung des Reststromes moderner Elektrolytkondensatoren, wenn er in einen Isolationswiderstand umgerechnet wird, deutlich kleiner ist als derjenige von Folien- oder Keramikkondensatoren, kann die Selbstentladung geladener Elektrolytkondensatoren mehrere Wochen dauern.

Dielektrische Absorption

Die Dielektrische Absorption ist eine unerwünschte Ladungsspeicherung des Dielektrikums. Wird ein Kondensator kurz entladen, entsteht an den Elektroden nach einigen Sekunden bis Minuten wieder ein Teil der vorher angelegten Spannung. Das Dielektrikum hatte einen Teil der Ladung absorbiert und gibt ihn nun nach und nach wieder frei. Dieser Nachladeeffekt ist als dielektrische Absorption oder als dielektrische Relaxation bekannt. Die Größe der Absorption wird im Verhältnis zur ursprünglich angelegten Spannung angegeben und hängt von dem verwendeten Dielektrikum ab.

Kondensatortyp	Dielektrische Absorption
Kunststoff-Folienkondensatoren, Polyesterdielektrikum	0,2 bis 0,25 %
Kunststoff-Folienkondensatoren, Polypropylendielektrikum	0,01 bis 0,05 %
Keramikkondensatoren, X7R	0,6 bis 1 %
Keramikkondensatoren, Z5U	2,0 bis 2,5 %
Aluminium-Elektrolytkondensatoren	etwa 10 bis 15 %

Abhängig vom Kondensatortyp können solche Nachladungen bis zu 15 % der vorher angelegten Spannung erreichen. Das kann unter Umständen zu relativ hohen Spannungen (sogar einige Volt) führen, die eine Gefährdung darstellen können: Es können dadurch Schäden an Halbleitern oder Funkenbildung beim Kurzschließen von Anschlüssen verursacht werden. Aber auch in Messschaltungen ist dieser Effekt eher unerwünscht, da er zu falschen Messergebnissen führt. Hochspannungs- und Leistungskondensatoren, auch größere Aluminium-Elektrolytkondensatoren werden daher kurzgeschlossen transportiert bzw. geliefert.

Streu- bzw. Parasitärkapazität

Aus physikalischen Gründen hat jedes reale elektrische Bauelement mehr oder weniger stark eine kapazitive Kopplung mit der Umgebung (Streukapazität) oder parallel zu seinem gewünschten Verhalten (Parasitärkapazität). Dieses kapazitive Verhalten kann vor allem bei hohen Frequenzen unerwünschte Auswirkungen haben.

Schaltungen, die an sich einen Kondensator benötigten, können aufgrund dieser schon vorhandenen Streukapazität zuweilen ohne einen Kondensator als separates Bauteil ausgeführt werden. Insbesondere können Kondensatoren im Picofaradbereich durch eine entsprechende Ausformung von Leiterzügen auf einer Leiterplatte ersetzt werden: Zwei gegenüberliegende Kupferflächen von 1 cm² haben bei einem Abstand von 0,2 mm beispielsweise bei Verwendung von FR4-Material (ε_r = 3,4) eine Kapazität von 15 pF. Die Realisierung solcher „Kondensatoren“ ist jedoch eine Preisfrage. Ein 15-pF-MLCC-Klasse-2-Keramikkondensator ist einschließlich der Bestückungskosten und abzüglich der von ihm benötigten Leiterplattenfläche deutlich preiswerter als 1 cm² Leiterplattenfläche.

Auch bei einem Kondensator können unerwünschte kapazitive Kopplungen entstehen. Insbesondere gewickelte Kondensatoren sind unsymmetrisch in Bezug auf die Außenfläche. An die außen liegende Schicht wird der „kalte“ Schaltungsteil (meist die Masse) angeschlossen, der das geringere oder niederohmigere Wechselspannungspotential führt, um eine Kopplung des Kondensators mit dem Umfeld zu verringern. Ähnlich verhält es sich mit Trimmkondensatoren, hier gilt das für den zur Trimmung betätigbaren Anschluss, um bei Betätigung mit einem Werkzeug dessen Störeinfluss zu verringern.

Siehe auch

• Frequenzkompensation

Literatur

• Friedhelm Schiersching: Kondensatoren verstehen und anwenden. Telekosmos-Verlag, Stuttgart 1983, ISBN 3-440-05185-4
• Otto Zinke, Hans Seither: Widerstände, Kondensatoren, Spulen und ihre Werkstoffe. Springer, Berlin 1982, ISBN 3-540-11334-7.
• Peter Volkmann, Edgar P. Vorndran: Elektrisches Feld und Kondensator. Aufgaben Elektrotechnik + Elektronik. Bd 2. VDE-Verl., Berlin 1999, ISBN 3-8007-2018-3.
• Wolfgang Just, Wolfgang Hofmann: Blindstromkompensation in der Betriebspraxis: Ausführung, Energieeinsparung, Oberschwingungen, Spannungsqualität. VDE-Verl., Berlin 2003, ISBN 3-8007-2651-3.
• Karsten Block, Block-Hölzel-Weigt-Zachert: Bauelemente der Elektronik und ihre Grundschaltungen. Einführung in die Elektronik. Teil 1. Stam, Troisdorf 1996, ISBN 3-8237-0214-9.
• H.-J. Bauckholt: Grundlagen und Bauelemente der Elektrotechnik. 3. Auflage, S. 389ff, ISBN 3-446-17047-2.
• DIN EN 60384-1
• Fritz Henze: Blindstrom und Leistungsfaktor. Fachbuchverlag Leipzig 1955

Weblinks

•  Commons: Kondensatoren – Sammlung von Bildern, Videos und Audiodateien
• Grundlagen und Funktionsweise
• Elektrisches Feld in Plattenkondensatoren (Animation)
• CapSite Technische Details zu industriell relevanten Kondensatoren (englisch)
• Technische Daten und weiterführende Informationen finden sich auf den Seiten der Hersteller, insbesondere: AVX, Cornell Dubilier, epcos,ELECTRONICON, Europe Chemi-Con, KEMET, Nichicon, Panasonic, RUBYCON, VISHAY, WIMA
• Daniel Bellan: Kondensatoren, TU Berlin Projektlabor Sommersemester 2005 (PDF-Datei; 148 kB)

Einzelnachweise

1. ↑ L. A. Vsevolozhskii, V. A. Filinov: Methods of measuring nonlinear capacity. In: Measurement Techniques. 19, Nr. 10, 1976, S. 1497–1500, doi:10.1007/BF01101215.
2. ↑ Capacitor. World of Invention, 27. Mai 2006, Abgerufen am 11. August 2009.
3. ↑ Patent DE92564: Elektrischen Flüssigkeitskondensators mit Aluminiumelektroden. Veröffentlicht am 19. Mai 1897, Erfinder: Charles Pollack (Patentnr. DRP 92564 auf DEPATISnet, abgerufen am 13. Dezember 2009).
4. ↑ Patent US2800616: Low voltage electrolytic capacitor. Veröffentlicht am 23. Juni 1957.
5. ↑ Matt Saltz: Capacitors: A Story of Dielectrics. Electronic News, 18. Januar 1999.
6. ↑ Parag Banerjee, Israel Perez, Laurent Henn-Lecordier, Sang Bok Lee, Gary W. Rubloff: Nanotubular metal-insulator-metal capacitor arrays for energy storage. In: Nature Nanotechnology. 4, Nr. 5, 2009, S. 292–296, doi:10.1038/nnano.2009.37.
7. ↑ Katherine Bourzac: Winzige Sandwiches für den großen Energiehunger. In: Telepolis. 20. Apr. 2009, abgerufen am 20. Apr. 2009. 
8. ↑ NanoCenter Improves Energy Storage Options. In: Nanotechnology Now. 23. März 2009, Abgerufen am 11. August 2009.
9. ↑ New Electrostatic Nanocapacitors Offer High Power and High Energy Density. In: Green Car Congress. 17. März 2009, Abgerufen am 11. August 2009.
10. ↑ exploding-bridgewire detonator, englische Wikipedia
11. ↑ Technische Dokumente der Fa. Jennings zu Vakuum-Kondensatoren
12. ↑ Technische Daten der Vakuum-Kondensatoren der Fa. Comet
13. ↑ Technische Übersicht über variable und feste Vakuumkondensatoren der Fa. Meiden
14. ↑ Übersicht und weiterführende Informationen der Fa. AVX zu Kondensatoren mit Glas-Dielektrikum
15. ↑ Datenblatt des „MOS Cap“ von AVX
16. ↑ [1] Technische Informationen zu SiO₂-Kondensatoren der Fa. Vishay
17. ↑ Leistungskondensatoren der Fa. EPCOS für unterschiedlichen Anwendungen
18. ↑ Produktbeschreibung von Leistungskondensatoren der Fa. ABB (englisch)
19. ↑ WVS-Technology, Vakuum-Kondensatoren
20. ↑ Ceramic Trimmer Capacitors. Murata, 27. August 2008, Abgerufen am 11. August 2009.
21. ↑ LASERtrim® SMT Tuner Capacitors. Johanson, Oktober 2008, Abgerufen am 11. August 2009 (Produktinformation).
22. ↑ Film Capacitors. General technical information. EPCOS, Mai 2009, Abgerufen am 11. August 2009 (PDF, 1,8 MB).
23. ↑ Umrechnung: 'Bandbreite in Oktaven' N in Gütefaktor Q und Gütefaktor Q in 'Bandbreite in Oktaven' N
24. ↑ Wolf-Ewald Büttner: Grundlagen der Elektrotechnik 2. Oldenbourg, 2004, ISBN 3486272969, S. 102.
25. ↑ ^{a b} S. P. Murarka, Moshe Eizenberg, A. K. Sinha: Interlayer dielectrics for semiconductor technologies. Academic Press, 2003, ISBN 9780125112215, S. 338–339.
26. ↑ K. W. Plessner: Ageing of the Dielectric Properties of Barium Titanate Ceramics. In: Proceedings of the Physical Society. Section B. 69, 1956, S. 1261–1268, doi:10.1088/0370-1301/69/12/309.
27. ↑ WIMA: Induktivität und Eigenresonanz.
28. ↑ Ludwig-Maximilians-Universität München, Fakultät für Physik: Der Kondensator.
29. ↑ Siliziumkondensator, Vishay, HPC0603A
30. ↑ Simic Electronics, Chip Mica Capacitors
31. ↑ AVX, NP0, 1000 pF 100 V, 0805, Q >= 1000 (1 MHz), [2]
32. ↑ Murata, C0G, 100 nF 50 V, 1206, Q > 1000/1 kHz, [3]
33. ↑ Holystone, HCC, X7R, Y5V, 0805, 100 nF 25 V
34. ↑ Wima,, FKP3, 100 nF 63 V, MKS4, 100 nF 50 V, SMD-PEN, 100 nF 63 V, , MKI2, 100 nF 63 V, [4]
35. ↑ Murata, X5R, 100 µF 6,3 V, 1206, Tan d 0,15/120Hz, Y5V, 100 µF 6,3 V, 1206, Tan d 0,2/100Hz, http://search.murata.co.jp/Ceramy/image/img/A18X/E0000026.pdf
36. ↑ Kemet, Produktsuche, T491, T510, T520, T530, A700, 100/10 http://www.kemet.com/kemet/web/homepage/kechome.nsf/weben/products
37. ↑ Sanyo, Os-Con, SMD-SVP, 120/10, http://www.edc.sanyo.com/pdf/e046.pdf
38. ↑ Panasonic, SMD-FP, 150/10, http://www.panasonic.com/industrial/components/capacitive/cap_smtelec.htm
39. ↑ Jianghai, CD 263 BK, 1000/10, 10x16 mm, http://xcnet.de/projekte/xnetcreate.de_v2/pics/kunden/dateimanager/5221/JE8_CD_263_BK.pdf
40. ↑ Das Elektronik-Kompendium: Kondensatoren.
41. ↑ WIMA: Isolationswiderstand.

Dieser Artikel wurde am 7. Juni 2007 in dieser Version in die Liste der exzellenten Artikel aufgenommen.