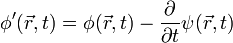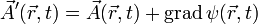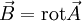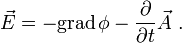Eichtransformationen

Dieser Artikel wurde aufgrund von inhaltlichen Mängeln auf der Qualitätssicherungsseite des Portals Physik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Physik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Hilf mit, die inhaltlichen Mängel dieses Artikels zu beseitigen, und beteilige dich an der Diskussion.

Als Eichtransformation bezeichnet man in der theoretischen Physik jede Transformation, in der eine frei wählbare Funktion als Transformationsparameter auftritt. Ist diese Funktion von den gewählten Koordinaten unabhängig spricht man von einer globalen andernfalls von einer lokalen Eichtransformation.

Folgen die Bewegungsgleichungen einer physikalischen Theorie aus einer Wirkung, die invariant unter Eichtransformationen ist, so spricht man von einer Eichtheorie und einer eichinvarianten Wirkung. Alle fundamentalen Wechselwirkungen, Gravitation, Elektromagnetismus, schwache Wechselwirkung (Beta-Zerfall des Neutrons) und die starke Wechselwirkung (Kernkräfte) werden durch Eichtheorien beschrieben.

Beispielsweise ist die Allgemeine Relativitätstheorie eine Eichtheorie, in der man neue Koordinaten als frei wählbare Funktionen der bisherigen Koordinaten verwenden kann.

Ebenso ist die Elektrodynamik eine Eichtheorie, deren Potentialfunktionen des elektrischen Feldes φ und des magnetischen Feldes 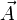$\vec{A}$ man um die partiellen Ableitungen einer beliebig wählbaren Funktion ψ abändern kann. Die Eichtransformation (in Maßsystemen mit c = 1)

$\phi'(\vec r, t) = \phi(\vec r, t) - \frac{\partial}{\partial t} \psi(\vec r, t)$

$\vec A'(\vec r, t) = \vec A(\vec r, t) + \mathrm{grad}\, \psi(\vec r, t)$

ändert weder das Magnetfeld

$\vec{B}=\mathrm{rot}\vec{A}$

noch das elektrische Feld

$\vec{E}=-\mathrm{grad}\,\phi-\frac{\partial}{\partial t} \vec{A}\ .$

Zur Definition von grad und rot siehe Gradient und Rotation.