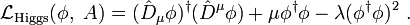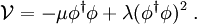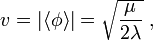- Higgs-Feld
-
Der Higgs-Mechanismus, nach dem britischen Physiker Peter Higgs benannt, ist Teil des Standardmodells der Elementarteilchenphysik. Er bietet eine Erklärung für die Beobachtung massiver Austauschteilchen, die in einer Eichtheorie wie dem Standardmodell der Elementarteilchenphysik zunächst nicht möglich scheinen.
In der relativistischen Quantenfeldtheorie versteht man unter dem Higgs-Mechanismus meist die Erzeugung der Massen der Wechselwirkungsteilchen in Eichtheorien durch spontane Brechung der Eichsymmetrie. Higgs und die anderen Entwickler dieses Mechanismus untersuchten dabei, wie bei der schwachen Wechselwirkung, vor allem den Fall nicht-abelscher Symmetriegruppen. Der Higgsmechanismus würde in diesem Fall die Massen der drei Eichbosonen Z0, W + und W − erklären.
Inhaltsverzeichnis
Vorbild in der Festkörpertheorie
Ein derartiger Mechanismus für die einfacheren abelsche Eichsymmetrien, wie bei der elektromagnetischen Wechselwirkung, wurde ursprünglich in der Festkörperphysik vorgeschlagen, um zu erklären, wie die Magnetfelder aus supraleitenden Metallen herausgedrängt werden (Meißner-Ochsenfeld-Effekt). Die endliche Eindringtiefe λ des Magnetfeldes kann so interpretiert werden, als hätte dieses Feld durch die Supraleitung eine effektive Masse Mλ bekommen, entsprechend der Beziehung λ = h / (Mλc), wobei h das Plancksche Wirkungsquantum und c die Lichtgeschwindigkeit ist.
Die 1950 veröffentlichte Ginzburg-Landau-Theorie der Supraleitung ist eine phänomenologische Theorie, die u.a. besagten Effekt vollständig beschreibt, nichttriviale weitreichende Konsequenzen hat und für die Übersetzung in die Hochenergiephysik besonders geeignet ist, obwohl sie im Unterschied zur mikroskopischen BCS-Theorie von 1957 die Existenz von Cooper-Paaren noch nicht voraussagte. (Analog ergibt der experimentelle Existenz-Nachweis des Higgs-Mechanismus noch keine mikroskopische Erklärung für die Natur des Higgs-Teilchens, d.h. für dessen Eigenschaften. Gegenwärtig, 2008, ist ja noch nicht einmal dessen Masse bekannt. Nachträglich könnte sich das Higgs-Teilchen, ähnlich wie die Cooper-Paare der Supraleitung, als „zusammengesetzt“ erweisen, etwa aus zwei schwach aneinander gebundenen W-Bosonen. Dann hätte das Higgs-Teilchen eine Masse von ungefähr 2 x 80 =160 GeV.)
Motivation in der Feldtheorie
Nach der Elementarteilchenphysik werden alle Kräfte durch den Austausch sogenannter Eichbosonen beschrieben. Dazu zählen z. B. die Photonen der Quantenelektrodynamik und die Gluonen der Quantenchromodynamik. Das Photon und die Gluonen sind masselos. Die Austauschteilchen der Schwachen Wechselwirkung, die W- und die Z-Bosonen, haben die im Vergleich zu Elektronen, Protonen und Neutronen großen Massen von ≈80 GeV/c² und ≈91 GeV/c². Diese sorgen unter anderem dafür, dass Teilchen, die gemäß der schwachen Wechselwirkung zerfallen, vergleichsweise lange Lebensdauern haben. Daher muss man in die Bewegungsgleichungen für diese Teilchen Massenterme einfügen. Da die Eichfelder, mit denen die Eichbosonen beschrieben werden, sich dann aber bei den so genannten Eichtransformationen ändern würden (es handelt sich dabei um lokale Symmetrien), geht das nicht. Denn die Eigenschaften der Grundkräfte beruhen gerade darauf, dass die Bewegungsgleichungen sich bei Eichtransformationen nicht ändern; das bezeichnet man als „Eichkovarianz“ der Bewegungsgleichung. Massenterme für die Eichfelder würden also das Kraftgesetz zerstören.
Spontane Symmetriebrechung
Man verwendet das Prinzip der so genannten spontanen Symmetriebrechung, um einerseits das Kraftgesetz zu erhalten und andererseits den Eichbosonen Masse zu geben. Dazu führt man ein zusätzliches Feld ein, nämlich das sogenannte Higgs-Feld. Dieses Feld wechselwirkt mit allen anderen Feldern und mit sich selbst, und zwar so, dass dadurch die Eichbosonen Masse erhalten.
Im Falle globaler Symmetrien hat die spontane Symmetriebrechung nach dem Goldstone-Theorem die Existenz masseloser Goldstonebosonen zur Folge. Das Goldstone-Theorem lässt sich jedoch nur auf globale Symmetrien anwenden.
Die Brechung lokaler Symmetrien wird mit dem Higgs-Mechanismus beschrieben, bei dem Goldstone-Bosonen bei den Eichfeldern nicht in Erscheinung treten. Stattdessen werden die Goldstone-Moden des Higgsfeldes zu longitudinalen Polarisationsfreiheitsgraden der Eichfelder und diese werden zugleich massiv. In der Quantenelektrodynamik (QED), die bekanntlich „nicht-massiv“ ist und bei der kein Higgsfeld auftritt, hat das Photon als masseloses Spin-1 Feld nur die zwei transversalen Polarisationsfreiheitsgrade.
Higgs-Potential (mit Veranschaulichung)
Die Lagrange-Dichte des Higgs-Feldes Φ, mit der (direkt sichtbaren) Selbstwechselwirkung und der (nur indirekt sichtbaren, weil nur in den
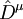 bzw.
bzw. 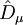 enthaltenen) Kopplung an Eichfelder A, die teilweise durch die Wechselwirkung mit dem Higgs-Feld zu massiven Austauschteilchen werden, lautet:
enthaltenen) Kopplung an Eichfelder A, die teilweise durch die Wechselwirkung mit dem Higgs-Feld zu massiven Austauschteilchen werden, lautet:Dabei sind μ und λ positive reelle Zahlen und
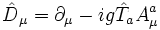 die sog. eichkovariante Ableitung, wobei die
die sog. eichkovariante Ableitung, wobei die 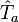 die Generatoren der Eichgruppe sind und die komplexen Funktionen
die Generatoren der Eichgruppe sind und die komplexen Funktionen 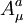 die Eichfelder.
die Eichfelder.An dieser Lagrange-Dichte ist noch nicht erkennbar, wie die Massen der Eichfelder zustande kommen. Dazu ist eine gesonderte Betrachtung des Potentials des Higgs-Feldes,
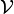 , hilfreich:
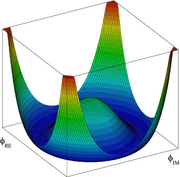
, hilfreich:Für ein reelles Feld Φ mit nur einer Komponente würde das Potential eine w-förmige Parabel vierter Ordnung beschreiben. Da Φ jedoch in allen Anwendungen komplex ist, kann man sich
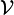 dreidimensional als Rotationsfigur dieser Parabel vorstellen, deren Form mit dem Boden einer Sektflasche vergleichbar ist (man spricht auch von Mexikanerhut-Potentialen). Wenn Φ mehr als eine komplexe Komponente hat, kann man sich die Form des Potentials nur noch bedingt so einfach anschaulich machen wie in dem nebenstehenden Bild.
dreidimensional als Rotationsfigur dieser Parabel vorstellen, deren Form mit dem Boden einer Sektflasche vergleichbar ist (man spricht auch von Mexikanerhut-Potentialen). Wenn Φ mehr als eine komplexe Komponente hat, kann man sich die Form des Potentials nur noch bedingt so einfach anschaulich machen wie in dem nebenstehenden Bild.Seine wichtigste Eigenschaft ist jedoch immer gleich: Es hat mindestens einen zweidimensionalen Kreis solcher Minima, die nicht bei Null liegen, sondern den tiefsten Zuständen des Flaschenbodens entsprechen. Die Minima des Potentials sind der günstigste Energiezustand für das Feld, weil es dort die niedrigste Energie hat. Man bezeichnet den Grundzustand als „Vakuum-Zustand“. Das Higgs-Feld hat also viele äquivalente Grundzustände, weil das Potential viele Minima mit gleicher Energie hat. Man spricht deshalb von einem „entarteten Grundzustand“.
Der Betrag von Φ im Grundzustand ist der sogenannte Vakuumerwartungswert
der sich durch Berechnen der Extremstellen des Potentials ergibt. Man kann nun das Higgs-Feld so definieren, dass genau so viele Komponenten wie man Eichfelder hat, denen man Masse geben will, von einer Nullstelle ausgehend die Nullstellenmenge nicht verlassen. Bei einem einkomponentigen komplexen Feld, bei dem man sich das Potential als unteren Teil einer Sektflasche vorstellen kann, ist diese Komponente also eine Winkelkomponente, so dass man für jeden Wert in dieser Komponente an einer anderen Stelle des Minimakreises herauskommt. Diese Komponenten ändern die Energie des Higgs-Feldes nicht; sie entsprechen bei globalen Symmetrien den Goldstone-Moden und können im Fall von Eichtheorien durch Auswahl einer Eichung festgelegt werden, so dass die Massenterme für die Eichbosonen in der Wirkung offensichtlich werden:
Der endliche Vakuumerwartungswert ergibt mit den Eichfeld-Termen aus den kovarianten Ableitungen (d.h. mit der kinetischen Energie, dem ersten Ausdruck von ) die Massenterme für die Eichfelder, nämlich Beiträge der Form
) die Massenterme für die Eichfelder, nämlich Beiträge der Form 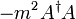 , mit
, mit 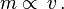
Die verbleibenden Komponenten ändern im Gegensatz zu den Goldstone-Moden des Higgs-Feldes die Energie, entsprechen also massiven Anregungen. Man fasst sie als Teilchenfelder auf, die als Higgs-Bosonen bezeichnet werden.
Weitere Auswirkungen
Eine Wechselwirkung des Higgs-Feldes Φ mit den Fermionfeldern ψ des Standardmodells verleiht möglicherweise auch den Quarks und Leptonen ihre Masse. Die Wechselwirkung des Higgs-Feldes mit den Fermionfeldern wird als Yukawa-Wechselwirkung angenommen, wodurch die Analogie zur Erzeugung der Atomkern-Eigenschaften durch Wechselwirkung der Nukleonen (Fermionen!) mit den Pionen (Bosonen) in der ursprünglichen Arbeit von Yukawa betont wird. Die Lagrangedichte für die Wechselwirkung eines Fermionfeldes ψ mit dem Higgs-Feld (und dem Eichfeld) lautet
wobei das Eichfeld A wieder nur in Dμ eingeht, γμ die Dirac-Matrizen sind und Gψ der Parameter der schon erwähnten Yukawa-Kopplung mit dem Higgs-Feld ist. Auch hier geschieht die Massenerzeugung nach dem gleichen Prinzip: die Existenz eines endlichen Vakuumerwartungswertes
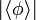 , dessen Ausbildung im vorigen Abschnitt beschrieben wurde, ist erneut das Wesentliche.
, dessen Ausbildung im vorigen Abschnitt beschrieben wurde, ist erneut das Wesentliche.Beispiele
Das Standardmodell der Elementarteilchen, insbesondere die Theorie der elektroschwachen Wechselwirkung wird durch solche Eichtheorien beschrieben. Der Vakuumerwartungswert des Higgsfeldes bricht im Standardmodell die lokale SU(2)xU(1)-Eichsymmetrie (zugehörige Erhaltungsgrößen: Schwacher Isospin und schwache Hyperladung) zur elektromagnetischen U(1)-Symmetrie (zugehörige Erhaltungsgröße: Elektrische Ladung). Drei Eichbosonen (die W- und Z-Bosonen) erhalten dabei eine Masse und einen longitudinalen Polarisationsfreiheitsgrad. Der 4. Freiheitsgrad des Higgsfeldes (welches als SU(2)-Dublett aus zwei komplexen = 4 reellen Feldern besteht) ergibt das Higgs-Boson.
Geschichte
Diese Theorie wurde 1964 von dem britischen Physiker Peter Higgs ausgearbeitet, basierend auf einem Vorschlag Philip W. Andersons. Unabhängig von Peter Higgs, haben auch Robert Brout und François Englert[1] 1964 an der Université Libre de Bruxelles schon vor Higgs sowie Gerald S. Guralnik, C. R. Hagen und T. W. Kibble[2] am Imperial College diesen Mechanismus entwickelt. Dennoch wird die Entdeckung meist allein Higgs zugeschrieben.
Ein ähnlicher Mechanismus wurde bereits 1957 von Ernst Stückelberg entwickelt.
Originalliteratur
- Peter Higgs: Broken symmetries, massless particles and gauge fields, in: Physics Letters 12, 1964, S. 132-133
- Peter Higgs: Broken symmetries and the masses of gauge bosons, in: Physical Review Letters 13, 1964, S. 508-509
Siehe auch
- Yang-Mills-Theorie, die mathematische Theorie der Eichbosonen, die durch den Higgs-Mechanismus Masse bekommen.
- Walter Greiner: Eichtheorie der schwachen Wechselwirkung. 1995, S. 133 ff..
Referenzen
- ↑ Broken Symmetry and the Mass of Gauge Vector Mesons. Physical Review Letters, Band 13, 1964, S. 321-323
- ↑ Global Conservation Laws and Massless Particles. Physical Review Letters, Band 13, 1964, S. 585-587
Weblinks
- Was ist ein Higgs-Teilchen?, Flash-Video aus der Fernsehsendung alpha-Centauri (JavaScript benötigt)
- Video aus der TU Graz über Higgs, SUSY, Strings
- A "popular" quasi-political Explanation of the Higgs Boson
- Animation zum Higgs-Mechanismus (Uni-Wuppertal)
- 'Englert-Brout-Higgs-Guralnik-Hagen-Kibble mechanism' auf Scholarpedia
Wikimedia Foundation.