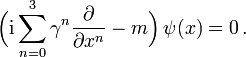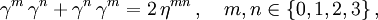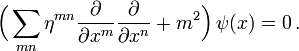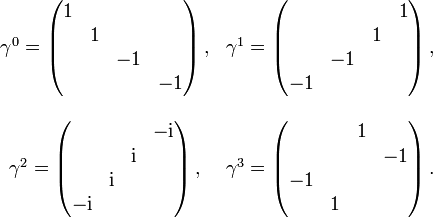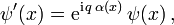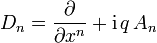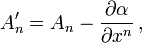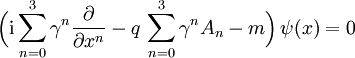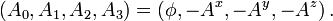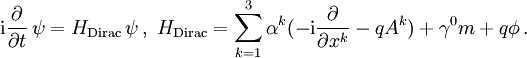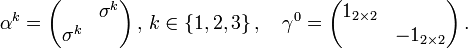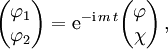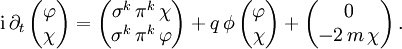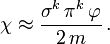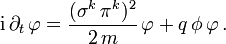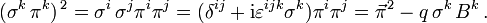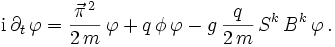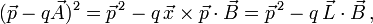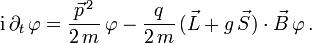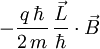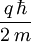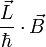- Diractheorie
-
Die Dirac-Gleichung beschreibt in der Quantenmechanik die Eigenschaften und das Verhalten des Elektrons (und anderer Spin-1/2-Teilchen) und berücksichtigt dabei die spezielle Relativitätstheorie. Sie wurde 1928 von Paul Dirac entwickelt.
Aus ihr ergibt sich die Existenz von Antiteilchen mit derselben Masse und demselben Spin, aber mit entgegengesetzter Ladung. So sagte Dirac 1931 das Antiteilchen des Elektrons, das Positron, ein Jahr vor seinem experimentellen Nachweis vorher.
Sie beschreibt die Feinstruktur des Wasserstoffspektrums.
Sie erklärt, warum sich der Spin des Elektrons wie ein kleiner Stabmagnet auswirkt, wenn beim Stern-Gerlach-Versuch ein Strahl von Silberatomen im inhomogenen Magnetfeld in zwei Teilstrahlen aufspaltet, je nach dem ob der Spin in Richtung oder Gegenrichtung des Magnetfeldes steht.
Für die Größe dieses Magneten im Vergleich zum Magnetfeld einer klassischen, kreisenden Punktladung sagt die Dirac-Gleichung den Wert g = 2 des gyromagnetischen Faktors voraus. Die theoretisch berechneten Korrekturen dieses Faktors betragen etwa ein Promille und stimmen in den ersten 10 Dezimalen mit dem gemessenen Wert überein.
Inhaltsverzeichnis
Dirac-Gleichung eines ungeladenen Teilchens
Die Dirac-Gleichung ist ein System von partiellen Differentialgleichungen für die Komponentenfunktionen
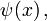 deren Zeit-und Ortsabhängigkeit in der Quantenmechanik den Zustand des Teilchens beschreiben. Die Zeit- und Ortskoordinaten (t,x,y,z) zählen wir durch oben stehende Zahlen ab und bezeichnen sie als (x0,x1,x2,x3) und zusammenfassend kurz als x.
deren Zeit-und Ortsabhängigkeit in der Quantenmechanik den Zustand des Teilchens beschreiben. Die Zeit- und Ortskoordinaten (t,x,y,z) zählen wir durch oben stehende Zahlen ab und bezeichnen sie als (x0,x1,x2,x3) und zusammenfassend kurz als x.In Maßeinheiten mit
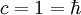 lautet die Dirac-Gleichung für ein ungeladenes Teilchen der Masse m
lautet die Dirac-Gleichung für ein ungeladenes Teilchen der Masse mHierbei sind die Gamma-Matrizen γ0,γ1,γ2 und γ3 Matrizen, die eine Clifford- oder Dirac-Algebra erzeugen. Das heißt, sie genügen den Gleichungen
wobei
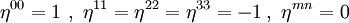 falls
falls 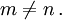
Mit der Dirac-Algebra zeigt man, dass bei Lorentztransformationen Lösungen der Dirac-Gleichungen in andere Lösungen übergehen, wenn man die Komponentenfunktionen wie die Komponentenfunktionen eines Spinors transformiert.
Wendet man
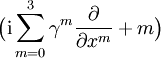 auf beide Seiten der Dirac-Gleichung an, dann zeigt sich mit der Dirac-Algebra, dass die Komponentenfunktionen ψ(x) auch der Klein-Gordon-Gleichung genügen,
auf beide Seiten der Dirac-Gleichung an, dann zeigt sich mit der Dirac-Algebra, dass die Komponentenfunktionen ψ(x) auch der Klein-Gordon-Gleichung genügen,Diese Gleichung entspricht der Energie-Impuls-Beziehung
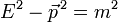 eines relativistischen Teilchens der Masse
eines relativistischen Teilchens der Masse 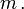
Da die Dirac-Gleichung ein Differentialgleichungssystem erster Ableitungsordnung ist, aus dem die Klein-Gordon-Gleichung mit ihren zweifachen Ableitungen folgt, wird sie auch als Wurzel der Klein-Gordon-Gleichung angesehen.
Mathematisch zeigt sich, dass jede irreduzible Darstellung der Dirac-Algebra aus
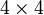 -Matrizen besteht. Es handelt sich also bei ψ um vier Komponentenfunktionen, deren Ableitungen in der Diracgleichung mit den γ-Matrizen multipliziert werden.
-Matrizen besteht. Es handelt sich also bei ψ um vier Komponentenfunktionen, deren Ableitungen in der Diracgleichung mit den γ-Matrizen multipliziert werden.In einer geeigneten Basis haben die Matrizen die folgende Form (wir schreiben verschwindende Matrixelemente nicht aus)
Diese Darstellung der γ-Matrizen heißt Dirac-Darstellung. In ihr lassen sich die Eigenschaften langsam bewegter Elektronen einfach bestimmen. In der dazu mathematisch und physikalisch äquivalenten Weyl-Darstellung ist das Spinor-Transformationsverhalten bei Lorentztransformationen einfach, in der ebenfalls äquivalenten Majorana-Darstellung ist die Dirac-Gleichung ein reelles Gleichungssystem.
Eichinvarianz und elektromagnetische Wechselwirkung
Wenn ψ(x) die Dirac-Gleichung löst, dann löst auch der mit einer Phase multiplizierte Spinor
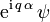 die Dirac-Gleichung. Da alle physikalisch messbaren Größen mit jedem Faktor ψ auch einen konjugiert komplexen Faktor ψ * enthalten, sind sie und die Dirac-Gleichung invariant unter dieser Phasentransformation des Dirac-Spinors ψ.
die Dirac-Gleichung. Da alle physikalisch messbaren Größen mit jedem Faktor ψ auch einen konjugiert komplexen Faktor ψ * enthalten, sind sie und die Dirac-Gleichung invariant unter dieser Phasentransformation des Dirac-Spinors ψ.Fordert man darüber hinaus die Invarianz unter allen Phasentransformationen, die stetig differenzierbar von Zeit und Ort abhängen,
dann muss man die Ableitungen in der Dirac-Gleichung zu sogenannten kovarianten Ableitungen
ergänzen. Die hier auftretenden vier Funktionen An heißen in der Physik Viererpotential oder Eichfeld, mathematisch handelt es sich um eine Konnektion oder einen Zusammenhang. Definiert man das transformierte Eichfeld durch
dann löst ψ die Dirac-Gleichung mit dem Eichfeld Am
genau dann, wenn der transformierte Dirac-Spinor die Dirac-Gleichung mit dem transformierten Eichfeld erfüllt. Transformationen, deren Parameter so wie hier die Phase α(x) beliebig von Zeit und Ort abhängen dürfen, heißen in der Physik Eichtransformationen.
Bei dem Eichfeld handelt es sich um das skalare Potential φ und das Vektorpotential
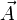 der Elektrodynamik,
der Elektrodynamik,Wenn man sie wie angegeben transformiert, bleiben die elektrische und magnetische Feldstärke,
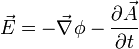 und
und 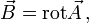
und alle anderen messbaren Größen unverändert.
Die Dirac-Gleichung mit kovarianten Ableitungen und die Elektrodynamik sind invariant unter beliebig zeit- und ortsabhängiger Transformation der Phase des Dirac-Spinors. Der Parameter q in der kovarianten Ableitung bestimmt die Stärke der Ankopplung der elektromagnetischen Potentiale an den Dirac-Spinor. Er ist die elektrische Ladung des Teilchens, das durch ψ beschrieben wird.
Die Ersetzung der partiellen Ableitungen in der Dirac-Gleichung durch kovariante Ableitungen koppelt die elektromagnetischen Potentiale an den Dirac-Spinor. Man spricht dabei von minimaler Kopplung im Gegensatz zu einem Kopplungsterm wie magnetischer Feldstärke mal Dirac-Spinor, der auch eichinvariant wäre, aber nicht zur Ergänzung einer Ableitung zu einer kovarianten Ableitung erforderlich ist.
Schrödingerform
Nach Multiplikation mit γ0 kann man wegen (γ0)2 = 1 in der Dirac-Gleichung nach der Zeitableitung auflösen und die Dirac-Gleichung in die Form einer Schrödinger-Gleichung bringen,
Die hier auftretenden Matrizen
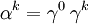 lassen sich kompakt mit Hilfe der Pauli-Matrizen mit Blöcken von
lassen sich kompakt mit Hilfe der Pauli-Matrizen mit Blöcken von 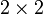 Matrizen schreiben:
Matrizen schreiben:Der Differentialoperator auf der rechten Seite der Schrödinger-Gleichung ist der zur Dirac-Gleichung gehörige Hamiltonoperator
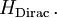 Die möglichen Energien des Teilchens sind Eigenwerte dieses Hamiltonoperators.
Die möglichen Energien des Teilchens sind Eigenwerte dieses Hamiltonoperators.Dabei zeigt die mathematische Untersuchung im Fall eines ungeladenen Teilchens (q = 0), dass das Spektrum positive und negative Werte enthält, ebenso wie man aus der Energie-Impuls-Relation der Klein-Gordon-Gleichung
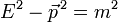 (in natürlichen Einheiten mit c = 1), die positiven und negativen Energiewerte
(in natürlichen Einheiten mit c = 1), die positiven und negativen Energiewerte 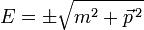 erhält.
erhält.Da Teilchen mit negativer Energie nie beobachtet wurden und da eine Welt mit Teilchen, deren Energien nach oben und nach unten unbeschränkt ist, instabil wäre, postulierte Dirac, dass das Vakuum ein Dirac-See sei, in dem jeder denkbare Zustand negativer Energie schon besetzt sei, so dass weitere Elektronen nur positive Energien annehmen könnten. Füge man diesem Dirac-See genügend Energie, mindestens die Ruheenergie zweier Elektronen, hinzu, so könne man einem See-Elektron positive Energie verleihen und das entstehende Loch verhielte sich wie ein Zustand mit der restlichen, ebenfalls positiven Energie und der fehlenden, entgegengesetzten Ladung. So sagte Dirac die Existenz von Antiteilchen und die Paarerzeugung von Elektron-Positron-Paaren voraus, die ein Jahr später beobachtet wurden.
Die Vorstellung eines Dirac-Sees gilt allerdings heute als unhaltbar [1] und ist durch die Feynman-Stückelberg-Interpretation ersetzt. Sie deutet die Dirac-Gleichung als Gleichung für ein Quantenfeld ψ(x), das ist mathematisch ein Operator, der in den quantenmechanischen Zuständen Teilchen oder Antiteilchen erzeugt oder vernichtet. Die Erzeugung und Vernichtung von Teilchen während der Wechselwirkung des Elektrons mit dem Proton führt in der Quantenelektrodynamik zu einer kleinen Verschiebung der Energien verschiedener Zuständen des Wasserstoffatoms, die ohne diese Erzeugungs-und Vernichtungsvorgänge gleiche Energie hätten. Die berechnete Größe dieser Lamb-Verschiebung stimmt innerhalb der Messgenauigkeit von sechs Stellen mit dem gemessenen Wert überein.
Die Erzeugung und Vernichtung von Teilchen während der Wechselwirkung des Elektrons mit einem Magnetfeld ändert auch den Dirac-Wert g = 2 des gyromagnetischen Faktors. Sie bewirkt ein sogenanntes anomales magnetisches Moment, von dem man auch als g − 2-Anomalie spricht. Der in der Quantenelektrodynamik berechnete Wert von g stimmt mit dem gemessenen Wert auf 10 Dezimalen überein.
Herleitung des gyromagnetischen Faktors
Wir gehen von der Schrödingerform der Dirac-Gleichung für ein Teilchen im elektromagnetischen Feld aus und spalten den Spinor in zwei Zweierspinoren auf. Dabei verwenden wir die Summationskonvention und schreiben die zu einem Indexpaar gehörige Summe nicht aus,
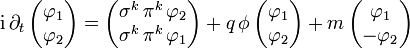 mit
mit 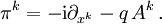
Wir unterstellen, dass sich das Teilchen nur langsam bewegt, so dass seine Energie nur wenig größer als die Ruheenergie ist. Das heißt, dass nach Abspalten der schnellen Zeitentwicklung, die von der Ruheenergie herrührt,
die Zeitableitungen der Zweierspinoren
 und χ klein sind,
und χ klein sind,In der zweiten Zeile ist nach Annahme die Zeitableitung klein und die kinetischen Energien und die elektrostatische Energie klein gegen die Ruheenenergie
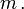 Daher ist χ klein gegen
Daher ist χ klein gegen  und ungefähr gleich
und ungefähr gleichIn die erste Zeile eingesetzt ergibt sich
Für das Produkt der Pauli-Matrizen erhält man
Der Spinor
 genügt daher der Pauli-Gleichung mit
genügt daher der Pauli-Gleichung mit 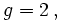
Dabei sind
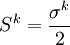 die Komponenten des Spin-Operators.
die Komponenten des Spin-Operators.Im homogenen Magnetfeld gilt
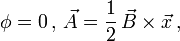 und mit
und mit 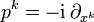
wenn man Terme vernachlässigt, die quadratisch in
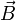 sind. Dann besagt die Pauli-Gleichung
sind. Dann besagt die Pauli-GleichungDas Magnetfeld koppelt folglich an den Bahndrehinpuls
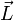 und trägt
und trägtzur Energie bei. Der Faktor
ist das Magneton des Teilchens. In Drehimpulseigenzuständen ist
ein ganzzahliges Vielfaches der Magnetfeldstärke
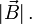
Siehe auch
Einzelnachweise
- ↑ J. Schwinger, A Report on Quantum Electrodynamics, in 'The Physicist's Conception of Nature', Reidel, Dordrecht, 1973, p. 415
Artikel
- P.A.M. Dirac: The Quantum Theory of the Electron. Proc. Roy. Soc. London A117, 610-624, 1928.
- P.A.M. Dirac: The Quantum Theory of the Electron, Part II. Proc. Roy. Soc. London A118, 351-361, 1928.
- P.A.M. Dirac: A Theory of Electrons and Protons. Proc. R. Soc. A126 360 (1930)
- C.D. Anderson: The Positive Electron. Phys. Rev. 43, 491-494 (1933)
- R. Frisch & O. Stern: Über das magnetische Moment eines rotierenden Wasserstoffmoleküls. Z. Phys. 85 4 (1933)
Bücher
- James Bjorken, Sidney Drell: Relativistische Quantenmechanik - Mannheim : Bibliographisches Institut, 1990. (BI Hochschultaschenbücher ; 98/98a) - ISBN ISBN 3-411-00098-8 -- engl. Originalausgabe: Relativistic Quantum Mechanics. McGraw-Hill, New York 1964, ISBN 0-07-005493-2
- James Bjorken, Sidney Drell: Relativistische Quantenfeldtheorie. [dt. Übers.: J. Benecke, D. Maison, E. Riedel]. - [Unveränd. Nachdr.] - Mannheim ; Zürich - BI-Wissenschaftsverlag, 1993. (BI-Hochschultaschenbuch ; 101 - ISBN 3-411-00101-1 -- engl. Originalausgabe: Relativistic Quantum Fields. McGraw-Hill, New York 1965, ISBN 0-07-005494-0
- Walter Greiner: Relativistische Quantenmechanik. Wellengleichungen. Band 6, ISBN 3-8171-1022-7
- Franz Schwabl: Quantenmechanik für Fortgeschrittene (QM II). ISBN 978-3-540-25904-6
Wikimedia Foundation.