Ellipsoidmethode

Die Ellipsoidmethode ist ein polynomialer Algorithmus zur Linearen Optimierung. Sie wurde ursprünglich in den Jahren 1976 und 1977 von David Yudin und Arkadi Nemirovski und unabhängig davon von Naum Schor zur Lösung konvexer Optimierungsprobleme entwickelt. Im Jahre 1979 wurde sie vom russischen Mathematiker Leonid Khachiyan zum ersten polynomialen Algorithmus zur Lösung linearer Programme erweitert. Damit bewies er erstmals die polynomiale Lösbarkeit linearer Optimierungsprobleme. Für praktische Zwecke ist die Ellipsoidmethode allerdings nicht geeignet.

Die Ellipsoidmethode ist ein Algorithmus zur Entscheidung, ob ein volldimensionales Polyeder der Form $P = \{x \in \mathbb{R}^n \;|\; A x \leq b\}$, wobei A eine reelle $m \times n$-Matrix und x,b dimensionskompatible Vektoren sind, leer ist oder nicht. Falls das Polyeder einen Punkt enthält, dann gibt die Methode auch einen solchen aus. Man kann zeigen, dass dieses Problem äquivalent zum Finden der Optimallösung eines linearen Programms ist.

Zwei Iterationen der Ellipsoidmethode

Der Algorithmus funktioniert folgendermaßen:

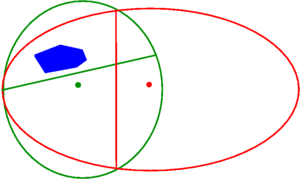
1. Es wird ein Ellipsoid (im Bild rot) bestimmt, welches – falls P (im Bild blau) nicht leer ist – einen Punkt des Polyeders enthält. Man kann dabei eine hinreichend große Kugel wählen, die alle möglichen Ecken von P enthalten muss. Deren maximale Koordinaten und damit der notwendige Radius der Kugel lässt sich durch Lösung von linearen Gleichungssystemen mit Einträgen aus A und b bestimmen.
2. Bestimmung einer maximalen Iterationsanzahl für folgende Schritte:
3. Es wird getestet, ob das Zentrum z (im Bild der rote Punkt) des Ellipsoids im Polyeder liegt (also $A z \leq b$)
4. Falls ja, wird z ausgegeben und der Algorithmus ist beendet.
5. Falls nein, sucht man eine Ungleichung (Schnittebene), die z vom Polyeder trennt. Dies kann zum Beispiel eine Zeile a_i der Matrix A sein, die a_iz > b_i erfüllt.
6. In dem Halbraum $\{x\in R^n \;|\; a_i (x-z) \leq 0\}$ liegt, falls das Polyeder nicht leer ist, ein Punkt von P. Nun sucht man ein Ellipsoid (im Bild grün), das möglichst klein ist, aber den Schnitt dieses Halbraums mit dem ursprünglichen Ellipsoid enthält.
7. Ist die maximale Iterationszahl erreicht, ohne dass ein Ellipsoidzentrum im Polyeder lag, ist dieses leer. Andernfalls macht man wieder bei 3. weiter.

Die maximale Iterationsanzahl berechnet sich polynomial aus der Länge der Binärcodierung der Matrix A und des Vektors b. Dieses Abbruchkriterium beruht darauf, dass das untersuchte Polyeder eine Mindestgröße haben muss, die von der Kodierungslänge von A und b abhängt. Wird diese Mindestgröße vom aktuellen Ellipsoid unterschritten, muss das Polyeder leer sein.

Siehe auch: Simplex-Verfahren