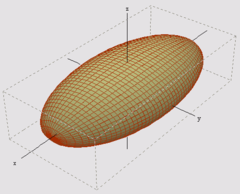
Ellipsoid

Triaxiales Ellipsoid mit (a,b,c) = (4,2,1)

Ein Ellipsoid ist die drei- oder mehrdimensionale Entsprechung einer Ellipse.

Bekannte Beispiele sind die Erde und der Rugbyball als Rotationsellipsoid.

Definition

Rugbyball als gestrecktes Rotationsellipsoid

Ein Ellipsoid im dreidimensionalen Raum kann als gestrecktes oder gestauchtes (affines) Bild einer Kugeloberfläche (Sphäre) erklärt werden. Unter Verwendung kartesischer Koordinaten und Ausrichtung der Koordinatenachsen x, y und z nach den Symmetrieachsen des Ellipsoids lautet seine Gleichung

$\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} - 1 = 0$

mit positiven reellen Zahlen a, b und c, den Längen der Halbachsen.

Im n-dimensionalen Raum ist ein Ellipsoid

$E= \left\{ x= (x_1\ldots x_n)^T\in R^n : x^T Q x = \sum_{1\le i,j\le n\ }q_{ij}x_i x_j = 1 \right\}$

die Lösungsmenge einer quadratischen Gleichung mit positiv definiter symmetrischer reeller (zu einer quadratischen Form gehörenden) Matrix Q = (q_ij).

Durch Hauptachsentransformation kann man Q auf eine Diagonalmatrix mit positiven Eigenwerten transformieren. Die Eigenvektoren dieser Matrix geben die Richtung der Hauptachsen an, die Kehrwerte der Wurzeln aus den Eigenwerten sind die Längen der zugehörigen Halbachsen.

In der Linearen Optimierung werden Ellipsoide in der Ellipsoid-Methode verwendet.

Die folgenden Erläuterungen beschränken sich wieder auf Ellipsoide im dreidimensionalen Raum. Sind alle drei Halbachsen verschieden, spricht man von triaxialen (oder dreiachsigen) Ellipsoiden. Bei Rotation einer Ellipse um eine ihrer Achsen entstehen Rotationskörper, in diesem Fall Rotationsellipsoide. Angenäherte Beispiele für Rotationsellipsoide sind rotierende Himmelskörper, etwa die Erde (vergl. Erdellipsoid) bzw. Planeten, Sonnen oder Galaxien. Elliptische Galaxien können auch triaxial sein.

Erde als Ellipsoid

Erde als gestauchtes Rotationsellipsoid

Die Erde ist nur ungefähr eine Kugel. In Wirklichkeit ist sie durch die Drehung um sich selbst an den Polen abgeflacht und auch sonst sehr unregelmäßig geformt. Um diese Unregelmäßigkeit genauer zu beschreiben, wird statt der Kugel oft ein Rotationsellipsoid verwendet. Dieses dient in der Kartografie und Geodäsie als Bezugssystem zur Konstruktion von Vermessungsnetzen und der direkten Angabe geografischer Koordinaten. Durch das Ellipsoid wird die Erdfigur als "Fläche konstanter Höhe" angenähert (siehe Geoid und Meeresspiegel).

Volumen des Ellipsoids

Das Volumen V lässt sich mit

$V = \frac{4}{3} \pi a b c$

aus dem Produkt der Halbachsen berechnen.

Oberfläche des Rotationsellipsoids

Sei $a \ge b \ge c$ und sei $\varepsilon = \sqrt{1 - \left(\frac{c}{a}\right)^2}$ die numerische Exzentrizität der Ellipse, die sich als Schnitt mit der xz-Ebene y = 0 ergibt. Dann ist für ein abgeplattetes (oblates) Ellipsoid mit a = b > c (Rotationsachse = z-Achse)

$A = 2 \pi a^2 \left( 1 + \left(\frac{c}{a}\right)^2 \,\frac{\operatorname{artanh} \,\varepsilon}{\varepsilon} \right)$

und für ein verlängertes (prolates) Ellipsoid mit a > b = c (Rotationsachse = x-Achse)

$A = 2 \pi c^2 \left( 1 + \frac{a}{c} \, \frac{\arcsin \,\varepsilon}{\varepsilon} \right).$

Oberfläche des triaxialen Ellipsoids

Die Oberfläche des triaxialen Ellipsoids lässt sich nicht mit Hilfe von Funktionen ausdrücken, die man als elementar ansieht, wie z. B. artanh oder arcsin. Die Flächenberechnung gelang Legendre mit Hilfe der elliptischen Integrale. Sei a > b > c. Schreibt man

$k=\frac ab \frac{\sqrt{b^2-c^2}}{\sqrt{a^2-c^2}}$ und $\varphi=\arcsin \frac{\sqrt{a^2-c^2}}{a}$,

so lauten die Integrale

$E(k,\varphi)=\int_0^{\sin \varphi} \sqrt{\frac{1-k^2 x^2}{1-x^2}}\ \mathrm dx$ und $F(k,\varphi)=\int_0^{\sin \varphi} \frac{1}{\sqrt{1-x^2}\sqrt{1-k^2 x^2}}\ \mathrm dx.$

Die Oberfläche hat mit E und F nach Legendre ^[1] den Wert

$A=2\pi c^2+\frac{2\pi b}{\sqrt{a^2-c^2}}\left(c^2 F(k,\varphi)+(a^2-c^2) E(k,\varphi)\right).$

Werden die Ausdrücke für k und φ sowie die Substitutionen

$u=\frac{\sqrt{a^2-c^2}}{a}$  und  $v=\frac{\sqrt{b^2-c^2}}{b}$

in die Gleichung für A eingesetzt, so ergibt sich die Schreibweise

$A=2\pi c^2+2\pi ab \int_0^1 \frac{1-u^2 v^2 x^2}{\sqrt{1-u^2 x^2} \sqrt{1-v^2 x^2}}\ \mathrm dx.$

Von Knud Thomsen stammt die (integralfreie) Näherungsformel

$A\approx 4\pi\!\left(\frac{ (a b)^{1,6}+(a c)^{1,6}+(b c)^{1,6} }{3}\right)^{0,625}\,\!.$

Die maximale Abweichung vom exakten Resultat beträgt weniger als 1,2%.

Im Grenzfall eines vollständig plattgedrückten Ellipsoids $\left( c \to 0 \right)$ streben alle drei angegebenen Formeln für A gegen 2πab, den doppelten Wert der Fläche einer Ellipse mit den Halbachsen a und b.

Herleitung der Formeln für Rotationsellipsoide

Mit den Definitionen der elliptischen Integrale E und F lassen sich die beiden rotationssymmetrischen Spezialfälle leicht aus der allgemeinen triaxialen Formel ableiten, denn E und F werden zu elementaren Funktionen.

Abgeplattetes Ellipsoid

b = a, also wird k = 1, daraus folgt $E(1,\varphi)=\int_0^{\sin \varphi} \ \mathrm dx =\sin \varphi = \frac{\sqrt{a^2-c^2}}{a}$ und $F(1,\varphi)=\int_0^{\sin \varphi} \frac{1}{1-x^2}\ \mathrm dx = \operatorname{artanh} (\sin \varphi) = \operatorname{artanh} \left(\frac{\sqrt{a^2-c^2}}{a}\right).$

Eingesetzt in Legendres Gleichung ergibt das $A = 2\pi c^2+\frac{2\pi a}{\sqrt{a^2-c^2}}\left(c^2 \operatorname{artanh}\left(\frac{\sqrt{a^2-c^2}}{a}\right) + (a^2-c^2) \frac{\sqrt{a^2-c^2}}{a}\right).$

Verlängertes Ellipsoid

b = c, also wird k = 0, daraus folgt $E(0,\varphi)= F(0,\varphi)=\int_0^{\sin \varphi} \frac{1}{\sqrt{1-x^2}}\ \mathrm dx = \arcsin (\sin \varphi) = \arcsin \left(\frac{\sqrt{a^2-c^2}}{a}\right).$

Eingesetzt in Legendres Gleichung ergibt das $A=2\pi c^2+\frac{2\pi c}{\sqrt{a^2-c^2}}\left(c^2 \arcsin \left(\frac{\sqrt{a^2-c^2}}{a}\right)+(a^2-c^2) \arcsin \left(\frac{\sqrt{a^2-c^2}}{a}\right)\right).$

Zusammenfassen und Vereinfachen führt auf die im Abschnitt Oberfläche des Rotationsellipsoids angegebenen Ausdrücke. Alternativ lassen sich die Oberflächen auch als Mantelflächen rotierender Ellipsen (Rotationsellipsoid) berechnen.

Siehe auch

• Hyperboloid
• Paraboloid
• Homöoid
• Fokaloid
• Referenzellipsoid in der Kartografie

Einzelnachweise

1. ↑ Legendre, Traite des fonctions elliptiques, Bd. 1, 1825, S. 357

Weblinks

 Wiktionary: Ellipsoid – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Online-Berechnung von Volumen und Oberfläche eines Ellipsoids (englisch)
• Herleitung der Formel für die Oberfläche eines Ellipsoids (englisch)