Endomorphismenmonoid

In der universellen Algebra ist ein Endomorphismus ein Homomorphismus 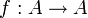$f: A \to A$ einer mathematischen Struktur A in sich selbst. Ist f zusätzlich ein Isomorphismus, dann wird f auch Automorphismus genannt.

In der Kategorientheorie heißt jeder Morphismus, dessen Quelle und Ziel übereinstimmen, ein Endomorphismus des fraglichen Objektes.

Die Gesamtheit der Endomorphismen eines Objektes A werden mit End(A) bezeichnet und bilden stets ein Monoid, in additiven Kategorien sogar einen (unitären) Ring.

Endomorphismen in der Linearen Algebra

In der linearen Algebra ist ein Endomorphismus ebenfalls ein Homomorphismus, also eine lineare Abbildung, 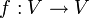$f :V \to V$. V meint hier jedoch ausschließlich K-Vektorräume. Diese Vektorraumendomorphismen haben die Eigenschaft, dass man sie als Matrixabbildung schreiben kann. Das heißt es gibt einen Vektorraumisomorphismus 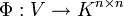$\Phi : V \to K^{n \times n}$. Dieser ist bis auf Basiswahl in 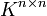$K^{n \times n}$ eindeutig bestimmt (siehe auch Basiswechsel). Es gibt also mehrere Matrizen, welche denselben Endomorphismus zu unterschiedlichen Basen beschreiben. Falls zwei Matrizen denselben Endomorphismus beschreiben, so haben sie dasselbe Minimalpolynom und damit auch dieselbe jordansche Normalform.

Beispiel

Das Differential 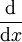$\frac{\mathrm{d}}{\mathrm{d} x}$ ist auf dem Vektorraum der Polynome R[x]₃ mit reellen Koeffizienten ein Endomorphismus. Als Basis von V wählt man die monomiale Basis {1,x,x²,x³}. Diese kann man isomorph auf die kanonische Basis des K⁴ abbilden, durch 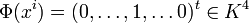$\Phi(x^i) = (0,\ldots, 1 , \ldots 0)^t \in K^4$. Die 1 steht dabei an der i-ten Stelle des 4-Tupel. Also kann man nun jedes Polynom aus R[x]₃ als 4-Tupel darstellen, so ist zum Beispiel Φ(4x³ + 2x + 5) = (4,0,2,5)^t. Nun kann man Φ mit 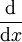$\frac{\mathrm{d}}{\mathrm{d} x}$ verketten und erhält für das Differential eine Matrixschreibweise:

$\Phi \circ \frac{\mathrm{d}}{\mathrm{d} x} \circ \Phi^{-1} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 3 & 0 & 0 & 0\\ 0 & 2 & 0 & 0 \\ 0 & 0 & 1 & 0\end{pmatrix}$.

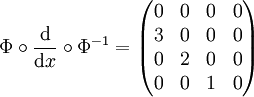Diese entspricht nun wieder dem Polynom 12x² + 2, welches man auch durch direktes Anwenden der Ableitung erhalten hätte.

Literatur

Gerd Fischer: Lineare Algebra, ISBN 3-528-03217-0