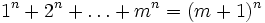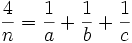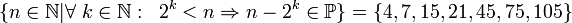Erdős-Vermutung

Der Mathematiker Paul Erdős hat in seinen Arbeiten viele Vermutungen in verschiedenen Bereichen der Mathematik aufgestellt.

Vermutungen im Gebiet der Zahlentheorie

• Erdős-Moser-Vermutung: Sie besagt, dass die Gleichung

$1^n+2^n+\ldots+m^n=(m+1)^n$

nur die Lösungen (n,m) = (0,1) und (1,2) hat.

• Erdős-Straus-Vermutung: Sie besagt, dass die Gleichung

$\frac4n=\frac1a+\frac1b+\frac1c$

für jede natürliche Zahl n > 1 eine Lösung in natürlichen Zahlen a,b,c hat.

• $\{n\in\mathbb{N}|\forall\; k\in\mathbb{N}:\;\; 2^k<n \Rightarrow n-2^k\in\mathbb{P}\} =\{4,7,15,21,45,75,105\}$

Betrachten wir die Menge S aller natürlichen Zahlen n mit folgender Eigenschaft:

Für jede natürliche Zahl k mit k>0 und 2^k < n ist n - 2^k eine Primzahl.

Dann enthält S sicherlich die Zahlen 4,7,15,21,45,75,105.

Zum Beispiel ist 45 in S, weil die Zahlen 45 − 2 = 43, 45 − 4 = 41, 45 − 8 = 37, 45 − 16 = 29, 45 − 32 = 13 alles Primzahlen sind.

Die Vermutung besagt nun, dass S nur aus diesen 7 Zahlen besteht.

Bis n = 2⁷⁷ ist diese Vermutung nachgerechnet worden, d.h. es gibt sicherlich keine Zahlen in S außer den genannten, die kleiner als 2⁷⁷ sind.

Jede Zahl n in S (außer 4) liefert automatisch einen Primzahlzwilling, nämlich (n − 2,n − 4).

Siehe auch: Folge A039669 in OEIS

Vermutungen im Gebiet der Graphentheorie

• Erdős-Faber-Lovász-Vermutung: Ein Graph, der eine Vereinigung vollständiger Graphen mit k Knoten ist, die paarweise höchstens einen Knoten gemeinsam haben, ist k-chromatisch.
• Erdős-Gyárfás-Vermutung: Jeder Graph, dessen Knoten alle mindestens Grad 3 haben, enthält einen Kreis, dessen Länge eine Zweierpotenz ist.