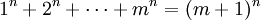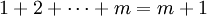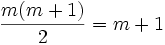Erdös-Moser-Gleichung — Die Erdős Moser Gleichung aus der Zahlentheorie ähnelt dem großen fermatschen Satz und lautet mit und . Für n = 0 ist die einzige Lösung m = 1 und für n = 1 ist die einzige Lösung m = 2. Weitere Lösungen sind nicht bekannt … Deutsch Wikipedia
Erdős-Moser-Gleichung — Die Erdős Moser Gleichung aus der Zahlentheorie ähnelt dem großen fermatschen Satz und lautet mit und . Für n = 0 ist die einzige Lösung m = 1 und für n = 1 ist die einzige Lösung m = 2. Weitere Lösungen sind nicht bekannt … Deutsch Wikipedia
Erdös-Vermutung — Der Mathematiker Paul Erdős hat in seinen Arbeiten viele Vermutungen in verschiedenen Bereichen der Mathematik aufgestellt. Vermutungen im Gebiet der Zahlentheorie Erdős Moser Vermutung: Sie besagt, dass die Gleichung nur die Lösungen (n,m) =… … Deutsch Wikipedia
Erdős-Vermutung — Der Mathematiker Paul Erdős hat in seinen Arbeiten viele Vermutungen in verschiedenen Bereichen der Mathematik aufgestellt. Vermutungen im Gebiet der Zahlentheorie Erdős Moser Vermutung: Sie besagt, dass die Gleichung nur die Lösungen (n,m) =… … Deutsch Wikipedia
Erdös — Erdős oder Erdoes ist der Familienname folgender Personen: Paul Erdős (1913–1996), österreichisch ungarischer Mathematiker Richard Erdoes (1912–2008), ungarisch österreichisch US amerikanischer Künstler Viktor Erdős (* 1987), ungarischer… … Deutsch Wikipedia
Erdős — oder Erdös ist der Name folgender Personen: Erich Erdös, österreichischer Eiskunstläufer Paul Erdős (1913–1996), österreichisch ungarischer Mathematiker Rudolf Erdös (1876−1935), österreichischer Architekt Viktor Erdős (* 1987), ungarischer… … Deutsch Wikipedia
Vermutungen von Paul Erdös — Der Mathematiker Paul Erdős hat in seinen Arbeiten viele Vermutungen in verschiedenen Bereichen der Mathematik aufgestellt. Vermutungen im Gebiet der Zahlentheorie Erdős Moser Vermutung: Sie besagt, dass die Gleichung nur die Lösungen (n,m) =… … Deutsch Wikipedia
Vermutungen von Paul Erdős — Der Mathematiker Paul Erdős hat in seinen Arbeiten viele Vermutungen in verschiedenen Bereichen der Mathematik aufgestellt. Vermutungen im Gebiet der Zahlentheorie Erdős Moser Vermutung: Sie besagt, dass die Gleichung nur die Lösungen (n,m) =… … Deutsch Wikipedia
Liste mathematischer Sätze — Inhaltsverzeichnis A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A Satz von Abel Ruffini: eine allgemeine Polynomgleichung vom … Deutsch Wikipedia
Hadwiger–Nelson-Problem — Das Hadwiger–Nelson Problem ist ein nach Hugo Hadwiger und Edward Nelson benanntes Problem der Geometrischen Graphentheorie. Gesucht wird die minimal benötigte Anzahl an Farben, um eine Ebene derart einzufärben, dass jeweils zwei Punkte mit… … Deutsch Wikipedia
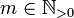 und
und 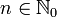 .
.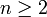 für eine Lösung der Gleichung
für eine Lösung der Gleichung  gelten muss. Er benutzte dazu Methoden der analytischen Zahlentheorie und kam ohne größere arithmetische Rechnungen aus. Durch massiven Rechnereinsatz konnten im Jahr 1999 bestimmte Zahlen genau berechnet werden, die Moser in seinem Beweis nur grob abgeschätzt hatte. Damit verbesserte sich die Schranke auf
gelten muss. Er benutzte dazu Methoden der analytischen Zahlentheorie und kam ohne größere arithmetische Rechnungen aus. Durch massiven Rechnereinsatz konnten im Jahr 1999 bestimmte Zahlen genau berechnet werden, die Moser in seinem Beweis nur grob abgeschätzt hatte. Damit verbesserte sich die Schranke auf 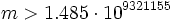 .
.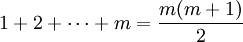 . Damit ergibt sich:
. Damit ergibt sich: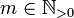 bleibt nur die zweite Lösung übrig.
bleibt nur die zweite Lösung übrig.