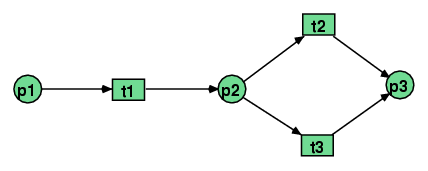
- Erreichbarkeitsgraph (Petri-Netz)
-
Ein Erreichbarkeitsgraph ist ein gerichteter Graph, der aus einem Petri-Netz und einer Anfangsmarkierung gewonnen werden kann. Er wird dadurch erzeugt, dass, mit der Anfangsmarkierung beginnend, die Menge der in der Markierung aktivierten Transitionen ermittelt und jeweils die Folgemarkierung berechnet wird. Die Markierungen werden durch Knoten im Erreichbarkeitsgraphen dargestellt und der Übergang einer Markierung zu ihrer Folgemarkierung wird als Kante im Graphen vermerkt. Für jede Folgemarkierung wird dieser Vorgang wiederholt.
Inhaltsverzeichnis
Formale Definition
Der Erreichbarkeitsgraph eines Netzes
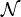 ist als
ist als 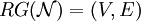 definiert, wobei V die Menge der Knoten und E die Menge der gerichteten Kanten des Graphen ist. V entspricht der Menge der von der Anfangsmarkierung aus erreichbaren Markierungen des Petri-Netzes. E besteht aus Tripeln (m,t,m'), wobei m eine von der Anfangsmarkierung aus erreichbare Markierung ist, von der durch Schalten der Transition t nach m' gelangt werden kann.
definiert, wobei V die Menge der Knoten und E die Menge der gerichteten Kanten des Graphen ist. V entspricht der Menge der von der Anfangsmarkierung aus erreichbaren Markierungen des Petri-Netzes. E besteht aus Tripeln (m,t,m'), wobei m eine von der Anfangsmarkierung aus erreichbare Markierung ist, von der durch Schalten der Transition t nach m' gelangt werden kann.Algorithmus zur Erzeugung des Erreichbarkeitsgraphen
Der folgende Algorithmus in Pseudocode erzeugt den Erreichbarkeitsgraphen eines Netzes
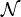 und der Anfangsmarkierung m0
und der Anfangsmarkierung m0function create_reachability_graph(N, m0) V := {} E := {} pending = {m0} while pending is not empty choose m from pending pending := pending \ {m} if m not in V V := V
 {m}
foreach transition t activated in m do
calculate m' such that
{m}
foreach transition t activated in m do
calculate m' such that 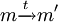 E := E
E := E  (m, t, m')
pending := pending
(m, t, m')
pending := pending  {m'}
{m'}
Analyse von Erreichbarkeitsgraphen
Mit Hilfe von Erreichbarkeitsgraphen lassen sich Petri-Netze analysieren. Beispielsweise lässt sich anhand des Erreichbarkeitsgraphen erkennen, ob ein Netz mit einer gegebenen Anfangsmarkierung lebendig ist. Ebenfalls lässt sich die Reversibilität des Netzes nachweisen oder widerlegen.
Beispiel
Betrachtet sei das folgende ungefärbte Petri-Netz mit der Anfangsmarkierung 2p1 + p2.
In der Anfangsmarkierung sind die Transitionen t1, t2 und t3 aktiviert.
1. IterationV = {2p1+p2, p1+2p2, 2p1+p3}
E = {(2p1+p2, t1, p1+2p2), (2p1+p2, t2, 2p1+p3), (2p1+p2, t3, 2p1+p3)}
2. IterationV = {2p1+p2, p1+2p2, 2p1+p3, 3p2, p1+p2+p3}
E = {(2p1+p2, t1, p1+2p2), (2p1+p2, t2, 2p1+p3), (2p1+p2, t3, 2p1+p3), (p1+2p2, t1, 3p2), (p1+2p2, t2, p1+p2+p3), (p1+2p2, t3, p1+p2+p3), (2p1+p3, t1, p1+p2+p3)}
3. IterationV = {2p1+p2, p1+2p2, 2p1+p3, 3p2, p1+p2+p3, 2p2+p3, p1+2p3}
E = {(2p1+p2, t1, p1+2p2), (2p1+p2, t2, 2p1+p3), (2p1+p2, t3, 2p1+p3), (p1+2p2, t1, 3p2), (p1+2p2, t2, p1+p2+p3), (p1+2p2, t2, p1+p2+p3), (2p1+p3, t1, p1+p2+p3), (3p2, t2, 2p2+p3), (3p2, t3, 2p2+p3), (p1+p2+p3, t1, 2p2+p3), (p1+p2+p3, t2, p1+2p3), (p1+p2+p3, t3, p1+2p3)}
4. IterationV = {2p1+p2, p1+2p2, 2p1+p3, 3p2, p1+p2+p3, 2p2+p3, p1+2p3, p2+2p3}
E = {(2p1+p2, t1, p1+2p2), (2p1+p2, t2, 2p1+p3), (2p1+p2, t3, 2p1+p3), (p1+2p2, t1, 3p2), (p1+2p2, t2, p1+p2+p3), (p1+2p2, t2, p1+p2+p3), (2p1+p3, t1, p1+p2+p3), (3p2, t2, 2p2+p3), (3p2, t3, 2p2+p3), (p1+p2+p3, t1, 2p2+p3), (p1+p2+p3, t2, p1+2p3), (p1+p2+p3, t3, p1+2p3), (2p2+p3, t2, p2+2p3), (2p2+p3, t3, p2+2p3), (p1+2p3, t1, p2+2p3)}
5. IterationV = {2p1+p2, p1+2p2, 2p1+p3, 3p2, p1+p2+p3, 2p2+p3, p1+2p3, p2+2p3, 3p3}
E = {(2p1+p2, t1, p1+2p2), (2p1+p2, t2, 2p1+p3), (2p1+p2, t3, 2p1+p3), (p1+2p2, t1, 3p2), (p1+2p2, t2, p1+p2+p3), (p1+2p2, t2, p1+p2+p3), (2p1+p3, t1, p1+p2+p3), (3p2, t2, 2p2+p3), (3p2, t3, 2p2+p3), (p1+p2+p3, t1, 2p2+p3), (p1+p2+p3, t2, p1+2p3), (p1+p2+p3, t3, p1+2p3), (2p2+p3, t2, p2+2p3), (2p2+p3, t3, p2+2p3), (p1+2p3, t1, p2+2p3), (p2+2p3, t2 3p3), (p2+2p3, t3, 3p3)}
In der letzten Markierung 3p3 ist keine Transition mehr aktiviert.Grenzen bei der Erzeugung von Erreichbarkeitsgraphen
Erreichbarkeitsgraphen lassen sich nur für beschränkte Netze vollständig berechnen. Für unbeschränkte Netze würde der Erreichbarkeitsgraph unendlich groß werden. In solchen Fällen werden häufig Überdeckungsgraphen konstruiert. Zwar lassen Überdeckungsgraphen in vielen Fällen keine Aussagen über die Reversibilität des Netzes zu, aber mit ihnen lassen sich andere Aspekte, wie zum Beispiel die Unbeschränktheit von Stellen, formal betrachten.
Siehe auch
Wikimedia Foundation.