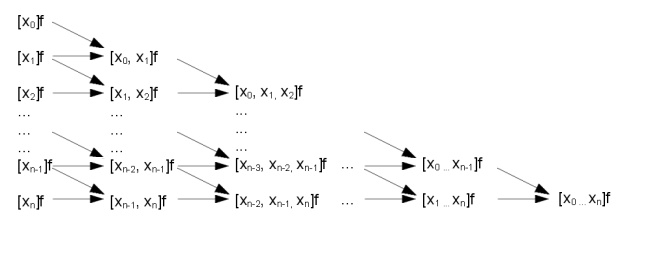
Aitken-Neville-Schema

Das Verfahren von Neville/Aitken kann zur Berechnung von Koeffizienten zur Polynominterpolation verwendet werden.

Für die numerische Berechnung ist dieser Algorithmus zu aufwändig. Das Verfahren der Dividierten Differenzen, welches weiter unten behandelt wird, ist für die numerische Berechnung deutlich besser geeignet.

Lemma von Aitken

Es bezeichne p(f | x_i...x_{i + k})(x) das eindeutig bestimmte Polynom k-ten Grades, das an den angegebenen Stellen x_j die jeweiligen Werte f_j annimmt. Dann gilt:

$p(f|x_0...x_n)(x) = \frac {(x_0 - x)\, p(f|x_1...x_n)(x) - (x_n - x) \,p(f|x_0...x_{n-1})(x)}{x_0-x_n}$

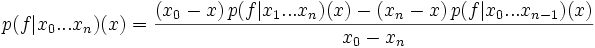
Der Beweis erfolgt durch Einsetzen von x_i, wodurch man verifiziert, dass die rechte Seite der Gleichung die Interpolationsbedingung erfüllt. Die Eindeutigkeit des Interpolationspolynoms liefert dann die Behauptung.

Schema von Neville

Da 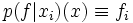$p(f|x_i)(x) \equiv f_i$ ein eindeutiges und bekanntes konstantes Polynom darstellt, lässt sich die Auswertung von p(f | x₀...x_n)(x) mit Hilfe des Lemmas von Aitken an einer Stelle x rekursiv berechnen. Dieses Schema wird als "Schema von Neville" bezeichnet.

Eine Auswertung benötigt also 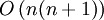$O\left({n(n+1)}\right)$ Operationen. Dies ist bei vielen Funktionsauswertungen des interpolierten Polynoms noch nicht optimal.

Dividierte Differenzen

Eine bessere Darstellung erreicht man durch sogenannte dividierte Differenzen. Es sei p(f | x_i...x_{i + k})(x) wieder das eindeutige Interpolationspolynom vom Grade k. Dann bezeichne den höchsten Koeffizienten dieses Polynoms mit [x_i...x_{i + k}]f und bezeichne ihn als "dividierte Differenz".

Mit Hilfe der Newton-Basis 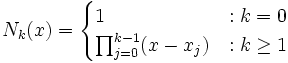$N_{k}(x) = \begin{cases} 1 & : k=0 \\ \prod_{j=0}^{k-1}(x-x_{j}) & : k\ge1 \end{cases}$ lässt sich das Interpolationspolynom eindeutig darstellen mittels

$p(f|x_{0}...x_{n})(x) = \sum_{k=0}^{n} [x_0...x_k]f \, N_k(x),$

wie man mittels vollständiger Induktion beweisen kann.

Schema der dividierten Differenzen

Die Auswertung des Polynoms dargestellt in der Newton-Basis kann sehr effizient mit dem Horner-Schema durchgeführt werden. Es bleibt, die dividierten Differenzen als Koeffizienten zu berechnen. Aus dem Lemma von Aitken folgt direkt die dazu benötigte Rekursionsformel (i > j):

$[x_i,...,x_j]f = \frac {[x_i,...,x_{j-1}]f-[x_{i+1},...,x_{j}]f}{x_i - x_j}$

Da [x_i]f = f_i gilt, lässt sich die Berechnung rekursiv durch das Schema der dividierten Differenzen durchführen:

Literatur

• Hans R. Schwarz, Norbert Köckler: Numerische Mathematik, 5. Aufl., Teubner, Stuttgart 2004, ISBN 3-519-42960-8.

Weblinks

• Anschauliches Beispiel zum Aitken und Neville Schema (pdf)