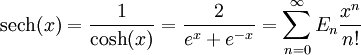Eulerzahlen

Die eulerschen Zahlen oder Euler-Zahlen (nach Leonhard Euler) sind eine Folge 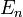$\, E_n$ ganzer Zahlen, die durch die Taylorentwicklung der Hyperbelfunktion Secans hyperbolicus

$\operatorname{sech}(x) = \frac{1}{\cosh(x)} = \frac{2}{e^x+e^{-x}} = \sum_{n=0}^{\infty} E_n \frac{x^n}{n!}$

definiert sind.

Eigenschaften

Alle eulerschen Zahlen mit ungeradem Index sind Null, während diejenigen mit geraden Index alternierende Vorzeichen haben. Die Dezimalen Endziffern von E_2n sind abwechselnd 1 und 5. Hier eine Wertetabelle der ersten Euler-Zahlen:

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
En	1	0	-1	0	5	0	-61	0	1385	0	-50521	0	2702765	0	-199360981	0	19391512145	0	-2404879675441	0

Für das asymptotische Verhalten der eulerschen Zahlen gilt $E_{2n}\sim (-1)^n\, 8\, \sqrt{\frac{n}{\pi}} \left(\frac{4n}{\pi e}\right)^{2n}$.

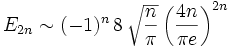Manche Autoren verschieben die Indizes so, dass E_2n zu E_n wird (da alle Euler-Zahlen mit ungeradem Index Null sind). Manchmal werden die eulerschen Zahlen auch so definiert, dass sie alle positiv sind.

Bedeutung

Die Folge der eulerschen Zahlen tritt zum Beispiel auch in der Taylorentwicklung von

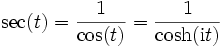$\sec(t)=\frac{1}{\cos(t)}=\frac{1}{\cosh(\mathrm{i}t)}$ auf.

Sie ist verwandt mit der Folge der Bernoullischen Zahlen.

Die eulerschen Zahlen treten daneben auch in der Kombinatorik auf. Auch in der Integralrechnung kommen sie vor; beispielsweise bei folgendem Integral

$\int\limits_0^\infty \frac{\ln^n(x)}{1+x^2}\, dx=|E_n|\left(\frac{\pi}{2}\right)^{n+1}$.

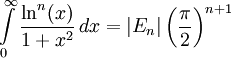Weblinks

• Eric W. Weisstein: Eulersche Zahlen auf MathWorld (englisch)
• Folge A122045 in OEIS