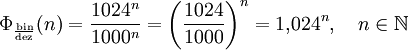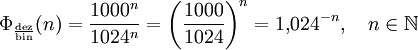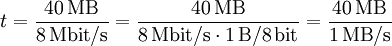Exbi

Die Artikel Binärpräfix und Byte#Präfixe für große Anzahlen von Bytes überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Carbenium 17:24, 7. Dez. 2008 (CET)

Binärpräfixe sind Vorsätze für Maßeinheiten (Einheitenvorsätze), die dazu verwendet werden, um Vielfache bestimmter Zweierpotenzen zu bezeichnen. Sie sind vorwiegend zur Verwendung mit Einheiten wie Bit (Symbol „bit“, auch „b“) oder Byte (Symbol „B“) gedacht, um Datenmengen zu bemessen, da hier aus technischen Gründen häufig Zweierpotenzen auftreten. Damit soll eine eindeutige Alternative zur mehrdeutigen Verwendung der SI-Präfixe für Zweierpotenzen zur Verfügung gestellt werden.

Definition der Binärpräfixe

Die Binärpräfixe sind gemäß der folgenden Tabelle definiert:

Name	Symbol	Wert
kibi	Ki	210 = 10241 = 1.024
mebi	Mi	220 = 10242 = 1.048.576
gibi	Gi	230 = 10243 = 1.073.741.824
tebi	Ti	240 = 10244 = 1.099.511.627.776
pebi	Pi	250 = 10245 = 1.125.899.906.842.624
exbi	Ei	260 = 10246 = 1.152.921.504.606.846.976
zebi	Zi	270 = 10247 = 1.180.591.620.717.411.303.424
yobi	Yi	280 = 10248 = 1.208.925.819.614.629.174.706.176

Beispiel: 512 MiB (Mebibyte) = 512 · 2²⁰ Byte = 536.870.912 Byte ≈ 537 MB (Megabyte).

Normen

Im Juni 1996 legte die Internationale elektrotechnische Kommission (IEC) einen Normentwurf für Binärpräfixe vor.^[1][2] Dieser Entwurf wurde im Dezember 1998 als Norm beschlossen und im Januar 1999 als Ergänzung zu IEC 60027-2 veröffentlicht.^[3] Er führte die Präfixe kibi, mebi, gibi, tebi, pebi und exbi für binäre Vielfache von Einheiten ein. In diesen Bezeichnungen wurden die ersten zwei Buchstaben der bereits genormten SI-Präfixe um „bi“ für „binär“ ergänzt. Für die Symbole der Binärpräfixe wurden die Symbole der SI-Präfixe verwendet und an diese der Kleinbuchstabe „i“ angehängt, wobei für das kibi im Gegensatz zum kilo der Großbuchstabe „K“ verwendet wurde. In der Norm wurde außerdem darauf hingewiesen, dass die SI-Präfixe nur für auf Zehnerpotenzen basierende Vielfache verwendet werden sollten. Diese Ergänzungen wurden in die im November 2000 veröffentlichte zweite Auflage der Norm IEC 60027-2 integriert. In die im August 2005 veröffentlichte dritte Ausgabe der Norm IEC 60027-2 wurden auch die Binärpräfixe zebi und yobi aufgenommen.^[4] Die Binärpräfixe werden inzwischen auch von anderen Normungsorganisationen unterstützt (z. B. IEEE 1541, BIPM/CIPM, NIST, CENELEC^[5], DIN/EN^[6][7], PTB^[8]).

Verwendung von SI-Symbolen für binäre Vielfache

In der Vergangenheit wurden mangels standardisierter Alternativen zur Bezeichnung von auf Zweierpotenzen basierenden Vielfachen häufig normwidrig SI-Präfixe verwendet, die den gewünschten Zweierpotenzen am nächsten kamen. Es sollte dann aus der Kombination mit den Einheiten Bit oder Byte oder einem anderen Kontext hervorgehen, dass eine Zweierpotenz gemeint war. Während dies bei Speicherbausteinen, die üblicherweise nur in Größen von Zweierpotenzen hergestellt werden, wenig problematisch ist, führte dies beispielsweise bei der Angabe von Festplattenkapazitäten in GB oder Datenübertragungsraten in MB/s oder Mbit/s zu Zweifeln hinsichtlich der genauen Bedeutung. Zudem wird die Abweichung bei höherwertigen Präfixen immer größer, sodass sie oft nicht mehr vernachlässigbar ist. Das für die SI-Präfixe zuständige Internationale Büro für Maß und Gewicht (BIPM) rät daher von dieser nicht normgemäßen Verwendung der SI-Präfixe ausdrücklich ab und empfiehlt für die Bezeichnung von Zweierpotenzen die Binärpräfixe gemäß IEC 60027-2.^[9] Trotzdem ist diese empfohlene Bezeichnungsweise auch heute (2008) noch nicht sehr weit verbreitet.

Die Werte der SI-Präfixe und der nächstliegenden Zweierpotenzen sind in der folgenden Tabelle dargestellt:

Name	Symbol	Wert gemäß SI	nächstliegende Zweierpotenz
Kilo	k	103 = 1.000	210 = 1.024
Mega	M	106 = 1.000.000	220 = 1.048.576
Giga	G	109 = 1.000.000.000	230 = 1.073.741.824
Tera	T	1012 = 1.000.000.000.000	240 = 1.099.511.627.776
Peta	P	1015 = 1.000.000.000.000.000	250 = 1.125.899.906.842.624
Exa	E	1018 = 1.000.000.000.000.000.000	260 = 1.152.921.504.606.846.976
Zetta	Z	1021 = 1.000.000.000.000.000.000.000	270 = 1.180.591.620.717.411.303.424
Yotta	Y	1024 = 1.000.000.000.000.000.000.000.000	280 = 1.208.925.819.614.629.174.706.176

Statt des SI-konformen Kleinbuchstabens „k“ wird auch der Großbuchstabe „K“ geschrieben (häufig nur als Ka gesprochen), um auf die beabsichtigte Abweichung von der Zehnerpotenz hinzuweisen. So kann „k“ für 1000 Einheiten verwendet werden und „K“ für 1024. Diese Konvention ist jedoch weder normiert noch wird sie konsequent angewendet. Zudem kann dieser Ansatz nicht auf die größeren Präfixe übertragen werden.

Verhältnis der binären und dezimalen Präfixe

Verhältnis bin/dez

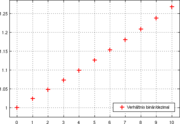
Die Werte der SI-Präfixe steigen in Zehnerpotenzen, weswegen die SI-Präfixe auch als dezimale Präfixe bezeichnet werden, während die Werte der Binärpräfixe in Zweierpotenzen ansteigen. Konkret steigen die Werte der dezimalen Präfixe – ausgehend von kilo – jeweils um den Faktor 10³ = 1000 und die Werte der binären Präfixe um den Faktor 2¹⁰ = 1024. D. h. kilo entspricht 1000¹, mega 1000², giga 1000³ usw., und kibi entspricht 1024¹, mebi 1024², gibi 1024³ usw. Beschreibt 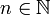$n \in\N$ die Präfixe derart, dass n = 1 für kilo und kibi steht, n = 2 für mega und mebi, n = 3 für giga und gibi usw., so ergeben sich die Werte der dezimalen Präfixe zu 1000ⁿ und die Werte der binären Präfixe zu 1024ⁿ. Aus dieser Tatsache lässt sich leicht eine Formel erstellen, welche das Verhältnis der Präfix-Werte zueinander angibt.

$\Phi_{\frac{\mathrm{bin}}{\mathrm{dez}}}(n) = \frac{1024^n}{1000^n} = \left(\frac{1024}{1000}\right)^n = 1{,}024^n, \quad n \in \N$

$\Phi_{\frac{\mathrm{dez}}{\mathrm{bin}}}(n) = \frac{1000^n}{1024^n} = \left(\frac{1000}{1024}\right)^n = 1{,}024^{-n}, \quad n \in \N$

Die folgende Tabelle gibt eine Übersicht über die sich daraus ergebenden Verhältnisse.

Name	Bin : Dez	Dez : Bin	Beispiel	Unterschied in %
Kilobyte, kibibyte	1,024	0,977	100 kB = 97,7 KiB	+2,4 % bzw. −2,3 %
Megabyte, mebibyte	1,049	0,954	100 MB = 95,4 MiB	+4,9 % bzw. −4,6 %
Gigabyte, gibibyte	1,074	0,931	100 GB = 93,1 GiB	+7,4 % bzw. −6,9 %
Terabyte, tebibyte	1,100	0,909	100 TB = 90,9 TiB	+10,0 % bzw. −9,1 %
Petabyte, pebibyte	1,126	0,888	100 PB = 88,8 PiB	+12,6 % bzw. −11,2 %
Exabyte, exbibyte	1,153	0,867	100 EB = 86,7 EiB	+15,3 % bzw. −13,3 %
Zettabyte, zebibyte	1,181	0,847	100 ZB = 84,7 ZiB	+18,1 % bzw. −15,3 %
Yottabyte, yobibyte	1,209	0,827	100 YB = 82,7 YiB	+20,9 % bzw. −17,3 %

Motivation und Geschichte

Ein wichtiger Bestandteil eines Computers ist der Arbeitsspeicher, der heute üblicherweise als Halbleiterspeicher realisiert wird. Die einzelnen Speicherzellen werden mit Hilfe von parallelen, binär arbeitenden Leitungen adressiert, die zusammengefasst als Adressbus bezeichnet werden. Mit einem Adressbus, der n Leitungen besitzt, können 2ⁿ Speicherzellen adressiert werden. Daher werden Halbleiterspeicher üblicherweise in Größen von Zweierpotenzen hergestellt. Mit zunehmender Größe der Speicher wurde es mangels standardisierter Alternativen üblich, SI-Präfixe mit den Speichereinheiten Bit und Byte zu verwenden, um Zweierpotenzen zu quantifizieren, obwohl die SI-Präfixe auf Zehnerpotenzen basieren. Bei Datenspeichern mit sequentieller Adressierung oder bei der sequentiellen Übertragung von Daten gibt es allerdings keinen Grund, mit Zweierpotenzen zu arbeiten, sodass hier die SI-Präfixe meist normgerecht verwendet werden. Dies hat zu einiger Verwirrung geführt, da teilweise auch für Fachleute nicht mehr eindeutig erkennbar ist, ob der jeweilige SI-Vorsatz normgerecht als Zehnerpotenz oder normwidrig als Zweierpotenz interpretiert werden soll.

Beispielsweise haben sich für die Bezeichnung „1 MB“ in der Praxis drei verschiedene Interpretationen eingebürgert:

• „1 MB“ = 1.000.000 B = 10⁶ B = 1000 kB – z. B. bei Festplatten und DVD-Medien;

• „1 MB“ = 1.048.576 B = 2²⁰ B = 1 MiB – z. B. bei Arbeitsspeicher (RAM, ROM, … ), Flash-Speicher, CD-Medien;

• „1 MB“ = 1.024.000 B = 1000 · 1024 B = 1024 kB = 1000 KiB – zur Kapazitätsangabe bei der klassischen 3½″-Diskette.

Außerdem findet sich noch die Bezeichnung „1 Mb“ (mit kleinem „b“ für „Bit“):

• „1 Mb“ = 1.000.000 b – bei der Datenübertragung, z. B. Telekommunikationsleitungen und Ethernet;
• „1 Mb“ = 1.048.576 b – bei Speicherbausteinen, z. B. „64-Mb-Chip“.

Diese inkonsequente Vorgehensweise kann beim Rechnen mit Einheiten zu schwer nachvollziehbaren Fehlern führen, wie an folgendem einfachen Beispiel gezeigt werden soll: Ein Computerbenutzer will eine Datei mit der angegebenen Größe von „40 MB“ aus dem Internet herunterladen und hat dazu eine Datenleitung mit einer Datenübertragungsrate von 8 Mbit/s zur Verfügung. Die zur vollständigen Übertragung dieser Datei benötigte Zeit lässt sich mit der Umrechnung 1 B = 8 bit (vereinfacht) folgendermaßen berechnen:

$t = \frac{ 40\,\mathrm{MB} }{ 8\,\mathrm{Mbit}/\mathrm{s} } = \frac{ 40\,\mathrm{MB} }{ 8\,\mathrm{Mbit}/\mathrm{s} \cdot 1\,\mathrm{B}/8\,\mathrm{bit} } = \frac{ 40\,\mathrm{MB} }{ 1\,\mathrm{MB}/\mathrm{s} }$

Hier drängt es sich auf, die „MB“ im Zähler gegen die „MB“ im Nenner zu kürzen, sodass sich ein Ergebnis von 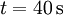$t = 40\,\mathrm s$ ergibt. Wenn jedoch mit dem „MB“ im Zähler eine Zweierpotenz gemeint ist, während im Nenner eine Zehnerpotenz gemeint ist, kann man diese Einheiten nicht gegeneinander kürzen, obwohl dies praktisch nicht mehr ersichtlich ist.

Für eine saubere Lösung dieses Problems gibt es mehrere Möglichkeiten:

1. Verzicht auf Präfixe;
2. ausschließliche und normgerechte Verwendung der SI-Präfixe;
3. (zusätzliche) Verwendung der von der IEC genormten Binärpräfixe für Zweierpotenzen.

Die Einführung der Binärpräfixe bedeutet nicht, dass sie die SI-Präfixe für die Verwendung mit Bits und Bytes ersetzen sollen. Beispielsweise kann man die Größe eines 536.870.912 Byte großen Arbeitsspeichers mit 536.870.912 B, 2²⁹ B, ca. 537 MB oder eben praktischerweise als 512 MiB angeben. Dadurch können die SI-Präfixe stets eindeutig in ihrer genormten Bedeutung verwendet werden.

Für die sehr weit verbreitete Angabe von Dateigrößen oder verfügbarem Festplattenspeicherplatz in Zweierpotenzen gibt es für die meisten Anwender keinen ersichtlichen Grund. Das Arbeiten mit Zweierpotenzen ist beispielsweise beim Addieren oder Subtrahieren von Datenmengen mit verschiedenen Binärpräfixen und beim Übergang auf größere oder kleinere Binärpräfixe ganz erheblich umständlicher als bei der Verwendung der auf das Dezimalsystem zugeschnittenen SI-Präfixe.

Akzeptanz und Verbreitung

Zumindest bis zum Januar 2002 wurden die IEC-Binärpräfixe in industrieller und wissenschaftlicher Literatur sowie in Software wenig beachtet und somit nur selten verwendet.^[10] Auch bis heute ist nur eine sehr langsam zunehmende Akzeptanz und Verbreitung festzustellen. Beispielsweise wird in den Informationen für Autoren des IEEE ausdrücklich auf die normgerechte Verwendung von SI-Präfixen hingewiesen.^[11] Das Computermagazin PC Games Hardware verwendet sie ab der Ausgabe 11/2007 (Erscheinungsdatum 2. Oktober 2007).^[12] Davon abgesehen gibt es mittlerweile einige Programme, welche die Binärpräfixe bereits unterstützen, z. B. der Linux-Kernel (und somit auch viele aktuelle Desktop-Distributionen) die GNU core utilities^[13], KDE 4, phpMyAdmin und einige BitTorrent-Programme.

Siehe auch

• Byte
• Vorsätze für Maßeinheiten
• Präfixe für große Anzahlen von Bytes

Weblinks

• BIPM: SI prefixes
• NIST: Prefixes for binary multiples
• IEC: Prefixes for binary multiples
• Alexey Chernyak: IEC prefixes and symbols for binary multiples
• Stefan Ram: Der Begriff „Kilobyte“ und ähnliche Begriffe

Einzelnachweise

1. ↑ International Electrotechnical Commission (IEC), new work item proposal 25/180/NP, Amendment of IEC 27-2: Letter symbols to be used in electrical technology, Part 2: Telecommunications and electronics – Introduction of prefixes for binary multiples, IEC/TC 25/WG 1, June 1996.
2. ↑ Markus Kuhn: Standardized units for use in information technology. 1996–12–29 [updated 1999-07-19]. [1]
3. ↑ Amendment 2 to IEC 60027-2: Letter symbols to be used in electrical technology – Part 2: Telecommunications and electronics.
4. ↑ IEC 60027-2, Ed. 3.0, (2005-08): Letter symbols to be used in electrical technology – Part 2: Telecommunications and electronics.
5. ↑ HD 60027-2:2003 Informationen zum CENELEC-Normierungsprozess.
6. ↑ prEN 60027-2:2006 Informationen zum EN-Normierungsprozess.
7. ↑ DIN EN 60027-2:2007-11 Beuth Verlag, Detailanzeige
8. ↑ Physikalisch-Technische Bundesanstalt: PTB-Mitteilungen 117 (2007), Heft 2, S. 22. „Das Internationale Einheitensystem”
9. ↑ BIPM – SI-Broschüre, 8. Auflage, März 2006, Abschnitt 3.1: SI-Präfixe. Randnotiz. [2]
10. ↑ tecCHANNEL: Von Kibibits und Gibibytes – Akzeptanz mangelhaft, 30. Januar 2002.
11. ↑ IEEE Periodicals, Transactions/Journals Department: Information for Authors. Revised: 1/06. (PDF, 943.576 B ≈ 943,6 kB ≈921,5 KiB)
12. ↑ Das Kibibyte kommt. In: PC Games Hardware Forum, 1. Oktober 2007.
13. ↑ Coreutils – GNU core utilities