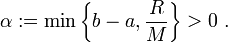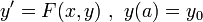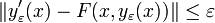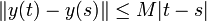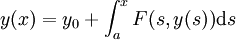- Existenzsatz von Peano
-
Der Satz von Peano ist ein Satz aus der Theorie der gewöhnlichen Differentialgleichungen. Er gibt eine einfache Voraussetzung an, unter der das Anfangswertproblem (mindestens) eine lokale Lösung besitzt. Dieser Satz wurde 1886 vom Mathematiker Giuseppe Peano mit einem fehlerhaften Beweis veröffentlicht. 1890 lieferte er einen korrekten Beweis nach.
Gegenüber dem Existenz- und Eindeutigkeitssatz von Picard-Lindelöf hat der Existenzsatz von Peano den Vorteil, dass er schwächere Voraussetzungen besitzt. Dafür macht er keine Aussage bezüglich der Eindeutigkeit der Lösung.
Besitzt man erst einmal eine (lokale) Lösung, kann man aus dieser in einem zweiten Schritt auf die Existenz einer nicht-fortsetzbaren Lösung schließen. In dieser Hinsicht ist der Satz von Peano ein erster Schritt für die Existenztheorie einer Differentialgleichung.
Formulierung
Sei
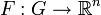 eine stetige Funktion. Ihr Definitionsbereich G sei eine
eine stetige Funktion. Ihr Definitionsbereich G sei eine ![[a,b] \times \overline{B}(y_0, R)](/pictures/dewiki/57/9e5dba8e2a1c6bd7fafdb141e8650208.png) umfassende Teilmenge von
umfassende Teilmenge von 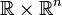 . Dabei bezeichne
. Dabei bezeichne 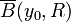 die abgeschlossene Kugel um
die abgeschlossene Kugel um 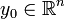 mit Radius R > 0, d.h.
mit Radius R > 0, d.h.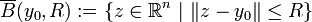 .
.
Dann gibt es zu jedem Anfangswertproblem
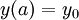 der Differentialgleichung
der Differentialgleichung 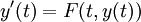 wenigstens eine lokale Lösung. Genauer heißt das, dass es ein α > 0 gibt und eine stetig differenzierbare Funktion
wenigstens eine lokale Lösung. Genauer heißt das, dass es ein α > 0 gibt und eine stetig differenzierbare Funktion ![y:[a,a+\alpha]\to \R^n](/pictures/dewiki/102/fced71a473c2800f426c10e0dabd2711.png) , die zwei Bedingungen erfüllt:
, die zwei Bedingungen erfüllt:- Für alle
![t\in[a,a+\alpha]](/pictures/dewiki/55/7b879fff3ec3ab6653c86267263b41f7.png) liegt der Punkt (t,y(t)) in G.
liegt der Punkt (t,y(t)) in G. - Für alle
![t\in[a,a+\alpha]](/pictures/dewiki/55/7b879fff3ec3ab6653c86267263b41f7.png) ist die Differentialgleichung
ist die Differentialgleichung 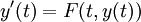 erfüllt.
erfüllt.
Ein solches α > 0 kann man genau angeben: Auf der abgeschlossenen und beschränkten Menge
![[a,b] \times \overline{B}(y_0,R)](/pictures/dewiki/57/9e5dba8e2a1c6bd7fafdb141e8650208.png) besitzt die stetige Funktion
besitzt die stetige Funktion 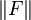 einen maximalen Wert, setze
einen maximalen Wert, setze![M := \max\{\|F(x,y)\|\ |\ (x,y) \in [a,b]\times \overline{B}(y_0,R)\}](/pictures/dewiki/100/d79348942d7f245f866b558b8e51793b.png) .
.
Diese Zahl ist eine Schranke für die Steigung einer möglichen Lösung. Man wähle nun
Dann existiert (mindestens) eine Lösung des Anfangswertproblems
auf dem Intervall
![\ [a,a+\alpha]](/pictures/dewiki/102/f0cfb5535a69748138a9434fba3a55e0.png) mit Werten in
mit Werten in 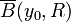 .
.Bemerkung: Analog können komplexe Differentialgleichungen betrachtet werden, indem man Real- und Imaginärteil einer komplexen Komponente als eigenständige reelle Komponente betrachtet, d.h., indem
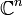 , die komplexe Multiplikation vergessend, mit dem
, die komplexe Multiplikation vergessend, mit dem 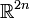 identifiziert wird.
identifiziert wird.Beweisskizze
Dieser Satz wird in zwei Teilen bewiesen. Im ersten Schritt besorgt man sich mit Hilfe des eulerschen Polygonzugverfahrens zu jedem
 spezielle
spezielle  -Näherungslösungen dieser Differentialgleichung, genauer: Man konstruiert eine stückweise stetig differenzierbare Funktion
-Näherungslösungen dieser Differentialgleichung, genauer: Man konstruiert eine stückweise stetig differenzierbare Funktion ![y_\varepsilon \in C([a,a+\alpha]; \overline{B}(y_0,R))](/pictures/dewiki/99/c26292fe651cf3f6288e01d7f1db1ce8.png) mit
mit 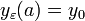 , welche
, welchein jedem Differenzierbarkeitspunkt erfüllt sowie die Gleichstetigkeitsbedingung
für alle
![s,t \in [a,a+\alpha]](/pictures/dewiki/49/1a4aa6f1a48e56fa223218da0e22da54.png) .
.Im zweiten Schritt zeigt man mit Hilfe des Satzes von Arzelà-Ascoli, dass es eine gleichmäßig konvergente Teilfolge
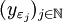 gibt. Von ihrer Grenzfunktion y zeigt man dann, dass sie die Integralgleichung
gibt. Von ihrer Grenzfunktion y zeigt man dann, dass sie die Integralgleichungerfüllt. Aus dem Fundamentalsatz der Analysis folgt dann, dass y stetig differenzierbar ist und der Differentialgleichung
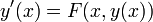 genügt.
genügt.
Literatur
- Herbert Amann: Gewöhnliche Differentialgleichungen. 2. Auflage. Gruyter - de Gruyter Lehrbücher, Berlin/New York 1995, ISBN 3-11-014582-0.
Wikimedia Foundation.