Giuseppe Peano

Giuseppe Peano

Giuseppe Peano (* 27. August 1858 in Spinetta, heute Teil von Cuneo, Piemont; † 20. April 1932 in Turin) war ein italienischer Mathematiker. Er arbeitete in Turin und befasste sich mit mathematischer Logik, mit der Axiomatik der natürlichen Zahlen (Entwicklung der Peano-Axiome) und mit Differentialgleichungen erster Ordnung.

Leben

Giuseppe Peano und seine Frau Carola Crosio im 1887

Peano war der Sohn von Bauern. Er besuchte die Schule in Cuneo und, als sein Talent erkannt wurde, ab 1870 das Gymnasium (Liceo) in Turin, wo ein Onkel Priester und Anwalt war. Ab 1876 studierte er Mathematik an der Universität Turin unter anderem bei Enrico D'Ovidio, Angelo Genocchi, Francesco Faà di Bruno und Francesco Siacci. 1880 promovierte er und wurde Assistent von D'Ovidio und danach bei Genocchi. Gleichzeitig erschien 1880 seine erste mathematische Arbeit. Er hielt die Analysis Vorlesungen von Genocchi (die auch 1884 als Buch herauskamen, herausgegeben, geschrieben und mit Zusätzen versehen von Peano). 1884 habilitierte er sich. Außer an der Universität hielt er auch Vorlesungen an der Militärakademie in Turin. 1890 wurde er Nachfolger von Genocchi als Professor an der Universität.

1891 begründete er die Zeitschrift Rivista di matematica, die sich vor allem den Grundlagen der Mathematik und der Logik widmete.

1892 begann er ein Projekt, die bekannten Sätze der Mathematik in logischer Strenge zu formulieren, das Formulario Matematico (beendet 1908), das er später auch für seine Vorlesungen benutzte, was ein pädagogischer Misserfolg wurde. 1901 wurde deshalb seine Lehrtätigkeit an der Militärakademie beendet. An der Universität konnte man ihm dagegen nicht hineinreden.

1900 fand Peano Anerkennung auf dem Internationalen Kongress für Philosophie in Paris.

Peano als Mathematiker

Vier Stufen einer Peano-Kurve

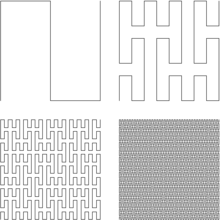
Peanos mathematisches Werk ist durch große logische Rigorosität geprägt. So hat er wiederholt Ausnahmefälle in veröffentlichten Theoremen gefunden (beispielsweise Arbeiten von Corrado Segre und Hermann Laurent). Auch die nach ihm benannte Peano-Kurve ist ein Beispiel hierfür. Sie ist eine stetige, surjektive Abbildung des Einheitsintervalls in das Einheitsquadrat, also eine raumfüllende Kurve, die definiert ist als der Grenzwert einer Folge von Kurven, die schrittweise konstruiert werden können. Vor Peano hatte man nicht mit der Möglichkeit der Existenz einer solchen Kurve gerechnet. Peano fand die Kurven 1890, wenig später gab David Hilbert weitere Beispiele.

Auch auf dem Gebiet der Analysis und der Differentialgleichungen hat Peano Wichtiges geleistet. Er fand das Restglied der Simpsonregel für die näherungsweise Berechnung von Integralen und bewies den Existenzsatz von Peano für gewöhnliche Differentialgleichungen (1886). Er fand auch unabhängig von Emile Picard dessen Näherungsverfahren zur Lösung von Systemen gewöhnlicher Differentialgleichungen (1887).

Peano hatte einen prägenden Einfluss auf die moderne Logik, Mengenlehre und Mathematik durch einige Werke, in denen er eine konsequente Formalisierung mathematischer Sachverhalte verfolgte. Peano erstellte in seinem Buch Calcolo Geometrico von 1888 erstmals ein Axiomensystem für den Vektorraum (wobei er unbeachtete Ideen von Hermann Grassmann aufgriff) und formulierte dort auch das moderne Axiomensystem für die boolesche Algebra, wobei er die Symbole $\cap$ und $\cup$ einführte. In seiner Arithmetik von 1889 stellte er - unabhängig von Dedekinds Arithmetik^[1] - die ersten formalen Axiome für die natürlichen Zahlen auf, die als Peano-Axiome berühmt wurden. Als Fundament für seine Arithmetik schuf er die erste formalisierte Klassenlogik, in der er unter anderem auch das Elementsymbol $\in$ und geordnete Paare (a, b) einführte. Die Formalisierung wichtiger logischer und mathematischer Gebiete baute er später in Formelsammlungen weiter aus; aus ihnen stammt unter anderem das Existenzquantorsymbol $\exist$.

1897 hielt er einen Plenarvortrag auf dem ersten Internationalen Mathematikerkongress in Zürich (Logica Matematica).

Peano als Linguist

Auf dem Gebiet der Linguistik machte sich Peano einen Namen, als er die Plansprache Latino sine flexione (= Latein ohne Beugung) schuf. Dies war ein Versuch, die ehemalige Weltsprache Latein wiederzubeleben, indem der weitgehend bekannte Wortschatz gewahrt wurde, die Schwierigkeiten der lateinischen Sprache aber weitgehend getilgt wurden. Dieses Latino sine flexione ging später in Interlingua auf.

Auch Teile seines Buchprojekts Formulario Matematico schrieb er in dieser Sprache.

Werke (Auswahl)

• Peano, Giuseppe: Calcolo geometrico, Torino 1888.
• Peano, Giuseppe: Geometric Calculus, translated by L. C. Kannenberg, Boston 2000.
• Peano, Giuseppe: Arithmetices principia nova methodo exposita, 1889, in: G. Peano, Opere scelte II, Rom 1958, 20-55
• Peano, Giuseppe: Logique mathematique, 1897, in: G. Peano, Opere scelte II, Rom 1958, 218-281
• Peano, Giuseppe: De latino sine flexione, 1903, in: G. Peano, Opere scelte II, Rom 1958, 439-447

Literatur

• Hubert C. Kennedy: Peano. Life and Works of Giuseppe Peano. Reidel, Dordrecht u. a. 1980, ISBN 90-277-1068-6 (Studies in the History of Modern Science 4).
• Hubert Kennedy: Giuseppe Peano. Biographie in deutscher Übersetzung von Ruth Amsler. Peremptory Publications, San Francisco CA 2002 (PDF; 241 KB).
• Hubert C. Kennedy: Giuseppe Peano. Birkhäuser, Basel u. a. 1974, ISBN 3-7643-0697-1 (Elemente der Mathematik. Beiheft 14).

Weblinks

• Literatur von und über Giuseppe Peano im Katalog der Deutschen Nationalbibliothek
• Giuseppe Peano. In: MacTutor History of Mathematics archive (englisch)
• Peano: Arithmetices principia nova methodo exposita als Online-Kopie.
• Online-Kopien verschiedener Schriften von Peano

Einzelnachweise

1. ↑ Hubert Kennedy: The origins of modern Axiomatics, in: American Mathematical monthly, 79 (1972), 133-136. Auch in: Kennedy: Giuseppe Peano, San Francisco, 2002, S. 15

Normdaten: PND: 11873976X (PICA) | LCCN: n80009883 | VIAF: 73925733 | WorldCat | WP-Personeninfo