Extremwertregelung

Der Extremwertregler ist ein Regler, der die Aufgabe hat eine oder mehrere Stellgrößen eines Systems so zu führen, dass eine Zielgröße, die aus einem oder mehreren Messwerten aus dem System gebildet wird, maximiert oder minimiert wird und dieser Optimalwert unter Einfluss von Störgrößen oder parametrischer oder struktureller Veränderungen des Systems gehalten wird.

Begriff

Im deutschsprachigen Raum hat sich der Begriff Extremwertregelung seit vielen Jahren etabliert. Im englischsprachigen Raum scheint es hingegen keine feste Begriffsdefinition zu geben. Durch ^[1] dürfte aber der Begriff extremum-seeking control der sein, der dieses Regelungsprinzip heute am häufigsten benennt. (s. jedoch auch ^{[Anm. 1]})

Einordnung in die Regelungstechnik

Auf Grund des Optimum-Charakters des Kennlinienfeldes der Strecke stellt der Extremwertregler immer ein Regler für nichtlineare Systeme dar. Er unterscheidet sich von allgemein gebräuchlichen Reglern dadurch, dass er keine Führungsgröße kennt und nur ein einziger Abtastpunktes auf der Messsignalseite keine Aussage liefert, in welche Richtung die Stellwerte verändert werden müssen, um in Richtung des Optimums zu gelangen, und wie groß die Entfernung zum Optimum ist. Um zumindest zur Richtungsinformation zu gelangen, sind immer zwei oder mehr Abtastungen auf dem Kennlinienfeld notwendig. Der Extremwertregler benötigt deshalb in seiner Struktur immer eine "suchende Komponente".

Zu beachten ist der funktionale Unterschied zur Adaptiven Regelung und zur Optimalen Regelung. Bei der Extremwertregelung werden nicht die Parameter oder die Struktur eines Reglers optimiert, um das System nach bestimmten Merkmalen optimal zu führen, sondern das System wird durch den Extremwertregeler so geführt, dass es selbst in einen Optimalpunkt seines Kennlinienfeldes fährt.^{[Anm. 1]}

Abb. 1: Allgemeinste Darstellung eines Extremwertregelkreises als Blockdiagramm

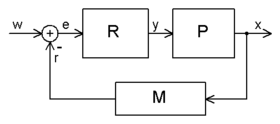
Abbildung 1 zeigt als Blockschaltbild die allgemeine Wirkungsweise eines Extremwertregelkreises. Darin bedeuten:

• R - Extremwertregler
• P - Prozess (umfasst Stelleinrichtung und zu regelndes System)
• M - Messeinrichtung (umfasst Sensorik, Signalwandlung und Signalbewertung)
• y - Stellwert
• x - Prozessgröße
• r - Rückführungsgröße

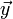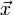Die Größen y und x können dabei allgemein auch als Vektoren $\vec y$ und $\vec x$ auftreten.

Abb. 2: Allgemeine Darstellung eines Regelkreises als Blockdiagramm

Dieses Blockschaltbild lässt sich zu der allgemeinen Darstellung eines Regelkreises (Abbildung 2) umformen, wenn die Führungsgröße w auf Null gesetzt wird. Das Summationsglied und die daraus resultierende Regelabweichung e wird bei einem Extremwertregler durch eine notwendige Struktur ersetzt, die die Lage des Extremwertes der Rückführgröße r mehr oder weniger genau abschätzt. Die Regelabweichung entspricht dabei sinngemäß der Entfernung und der Richtung vom momentanen Arbeitspunkt zum Extremwert. Im Vergleich ist bei dem allgemeinen Regelkreis eine Beschränkung auf einen skalaren Wert der Rückführgröße r nicht zwingend notwendig.

Zielgröße

Die Zielgröße der Extremwertregelung entspricht der skalaren Rückführgröße r in der allgemeinen Darstellung.^{[Anm. 2]} Die Zielgröße muss durch eine Bewertung aus den Messgrößen so bestimmt werden, dass deren Extremwert mit dem vom Anwender gewünschten optimalen Zustand des zu regelnden Systems übereinstimmt. Durch diese Bewertung ergibt sich dann der Zusammenhang

$r = f( \vec x )$

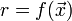
als Kennlinie bzw. -fläche mit einem Extremwert im optimalen Systemzustand.

Damit der Extremwertregler aus allen Arbeitspunkten im Stellbereich der Stellgrößen den Extremwert finden kann, darf sich in diesem Bereich nur ein lokales Extremum befinden. Im allgemeinen arbeiten die Extremwertregelungen auch bei Vorhandenseins eines Sattelpunktes, wenn im Maße der Auflösung der Messwerte und der "Suchbreite" im Arbeitspunkt der Gradient neben dem Sattelpunkt aufgelöst werden kann.^{[Anm. 3]}

Funktionsweise

Das Grundprinzip aller Extremwertregler besteht darin, dass im aktuellen Arbeitspunkt das Kennlinienfeld abgetastet wird. Dies kann kontinuierlich, quasikontinuierlich oder zeitdiskret erfolgen. Wird ein Gradient festgestellt, so wird der Arbeitspunkt "in Richtung" dieses Gradienten verschoben. Da im Optimum der Gradient genau Null ist, verharrt die Regelschleife in diesem Punkt, tastet ihn aber weiterhin ab. Verschiebt sich nun die Lage des optimalen Punktes, detektiert dies der Extremwertregler und folgt dem Optimalpunkt. Es gibt dabei Verfahren, wie der unten genannte Relais-Extremwertregler, die keinen expliziten Unterschied zwischen Gradientenabtastung und Arbeitspunkt machen und/oder auch keinen Zwischenwert bestimmen, der als Gradient interpretiert werden kann. Trotzdem beruhen diese Verfahren auf dem Gradient oder auf dessen Vorzeichen.

Bei der Auslegung eines Extremwertreglers ist zu beachten, dass die zu regelnden Systeme in der Regel dynamische Systeme sind. Weiterhin ist zwischen ein- und mehrdimensionalen Systemen zu unterscheiden. Von eindimensionalen Systemen wird gesprochen, wenn die Stellgröße ein skalarer Wert ist. Bei mehrdimensionalen Systeme hingegen ist die Stellgröße ein Vektor aus einer festen Anzahl von Stellwerten.

Abgrenzung zu Optimierungsverfahren

Durch das notwendige Verhalten der Extremwertregler, einen Optimalpunkt eines Systems zu finden und zu halten, haben sie nicht nur Ähnlichkeit mit den allgemein aus der Mathematik und anderen Wissenschaftsgebieten bekannten Optimierungsverfahren (s. Operations Research), sondern stellen selbst eine Teilmenge solcher Optimierungsverfahren dar.

Prinzipiell kann ein Extremwertregler mit vielen bekannten Optimierungsverfahren realisiert werden. (s. z.B. ^[2]) Im allgemeinen stellen jedoch die Ansprüche aus Sicht der Regelungstechnik meist Grenzen, die den Einsatz solcher Verfahren nicht zulassen oder zu Modifikationen führen, die die Effektivität dieser Verfahren stark beeinträchtigen.

Diese regelungstechnischen Ansprüche sind vor allem:

1. Kontinuierliches Verhalten
2. Stabilität im Arbeitspunkt
3. Begrenzter Stellbereich
4. Dynamisches Verhalten des zu regelnden Systems
5. Einfluss von Störsignalen auf der Zielgröße

Solche Optimierungsverfahren, die mit der Ableitung der Zielfunktion arbeiten, sind grundsätzlich nicht verwendbar, da im Falle der Extremwertregelung nur eine näherungsweise Bestimmung des Gradienten in einem Arbeitspunkt möglich ist, aber nicht die gesamte Funktion des Kennlinienfeldes als Gleichung oder Gleichungssystem bekannt ist.

Gute Optimierungsverahren sind dadurch gekennzeichnet, dass sie möglichst schnell bzw. mit möglichst geringem Rechenaufwand den Optimalpunkt finden. Aus diesem Grund arbeiten die meisten Verfahren mit einer Anpassung der Schrittweite, mit der das Kennlinienfeld abgetastet wird. Zu Beginn der Suche wird das Kennlinienfeld mit groben Schritten abgetastet und bei Annäherung an den Optimalpunkt diese Schrittweite sukzessiv verringert. In der Regel wird als Abbruchkriterium für "Optimalpunkt gefunden" eine Unterschreitung der Schrittweite durch diese Schrittweitensteuerung verwendet.

Diese Verhaltensweise steht im Widerspruch zu den oben genannten Ansprüchen 1 bis 4. Die Abtastwerte werden diskontinuierlich über einen großen Bereich des Kennlinienfeldes an den Stellen gewonnen, die das jeweilige Verfahren als sinnvollen Abtastpunkt für die schnelle Auffindung des Optimums vorausberechnet. Damit erfolgt die Abtastung nicht kontinuierlich, nicht im Bereich eines Arbeitspunktes, berücksichtigt nicht ohne spezielle Maßnahmen die Begrenzungen des Stellbereichs und kann das System, wenn es dynamisch ist, was in der Regel in technischen Systemen der Fall ist, so anregen, dass es in kritische Betriebszustände (Schwingungen, Begrenzungen) gelangt. Diesem kann zwar durch massive Begrenzung der Schrittweite entgegen gewirkt werden, jedoch verlieren dadurch diese Verfahren genau die Vorzüge, die sie zu einem schnellen Auffinden des Optimalpunktes bringen.

Viele mathematischen Verfahren sind außerdem für "glatte" Funktionsverläufe vorgesehen. Bei technischen Systemen hat man es jedoch immer mit einem Störpegel im Messsignal zu tun (Punkt 5). Vor allem im Bereich des Optimums, wo der Gradient des Kennlinienfeldes gegen Null geht, machen sich bei kleinen Abtastschritten diese Störungen erheblich bemerkbar, da sie dem Algorithmus "vorgaukeln", er befände sich nicht im Optimum. Eine Filterung der Messdaten bringt hier Abhilfe, was aber die Suchgeschwindigkeit gegenüber der theoretisch mit dem jeweiligen Verfahren möglichen Suchgeschwindigkeit weiter verringert. Allerdings stellt dies kein Unterschied zu den üblicherweise verwendeten Extremwertregelungsverfahren dar, da auch diese eine Glättung, meist durch Integration, durchführen.

Eine prinzipielle Unterscheidung in der Anwendung von Extremwertregelern gegenüber üblichen Optimierungsverfahren ist letztlich, dass es nicht nur darum geht, den Optimalpunkt zu finden (im Idealfall nur beim Einschalten des Regelkreises), sondern diesen über lange Zeit stabil zu halten.

Stabilität

Auch bei der Extremwertregelungen muss die Stabilität, wie in allen anderen Regelungssystemen auch, gewährleistet werden. Die Bedingungen sind mit Nichtlinearen Regelungen vergleichbar. Besondere Beachtung ist darauf zu richten, dass es hier aus dem Arbeitspunkt heraus nicht nur zu dem typischen "Aufschwingen" durch eine wirksame Schleifenverstärkung > 1 kommen kann, sondern dass sich der Arbeitspunkt selbst nicht stabil in den Extrempunkt bewegt bzw. dort verbleibt. Solches Verhalten kann bei falscher Auslegung auch ohne das typische Schwingungsverhalten von Regelungssystemen auftreten. Grund hierfür können Phasenverschiebungen zwischen dem Signal des Stellvektors und dem der Rückführung sein, wenn deren Verhalten zueinander zur Richtungsbestimmung (Gradientenabschätzung) im Extremwertregler verwendet wird.

Bekannte Extremwertregelungsverfahren

Wie bei den Optimierungsverfahren auch, lässt sich über die verschiedenen Formen der Extremwertregler kein umfassendes Abbild schaffen, da sich jedes Verfahren letztlich entsprechend des Anwendungsfalles in irgend einer Form weiterentwickelt lässt. In der folgenden Übersicht sollen deshalb die Grundverfahren genannt werden, auf die sich entsprechende Weiterentwicklungen zurückführen lassen.

Eindimensionale Extremwertregler

Die Dimension bezieht sich auf den Stellvektor, der bei diesen Verfahren eine skalare Größe sein muss. Alle im folgenden beschriebenen Verfahren sind für sich genommen nur auf solche eindimensionalen Probleme anwendbar. Wie diese für mehrdimensionale Probleme erweitert werden können: s. Mehrdimensionale Extremwertregler

• Relais-Extremwertregler

Mehrdimensionale Extremwertregler

Wenn der Regler gleichzeitig oder quasi gleichzeitig mehrere Stellgrößen so einstellen muss, dass eine Zielgröße in ihr Extremum geführt wird bzw. dort gehalten werden soll, handelt es sich um ein mehrdimensionales Verfahren.

Abb. 3: Mehrdimensionaler Extremwertregler mit unterlagertem eindimensionalen Extremwertregler

Wie bei den allgemeinen Optimierungsverfahren auch, gibt es für diese Aufgabe zwei prinzipiell verschiedene Lösungswege. Der erste Weg besteht darin, dass das Problem in ein eindimensionales Problem umgeformt wird, dass dann mit einem der oben genannten eindimensionalen Extremwertregler gelöst wird. Abbildung 3 zeigt ein solches Prinzip im Blockschaltbild.

Der unterlagerte eindemsionale Extremwertregler R_u wirkt dabei nicht direkt auf den Prozess, sondern wird mit einem Richtungsvector 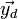$\vec {y_d}$ multipliziert. Diesen Richtungsvektor gibt der überlagerte Regler R vor, der dafür eine Bewertung von Größen aus dem unterlagerten Kreis durchführt und gegebenenfalls auch a priori Wissen über den Prozess verwendet. Vom strukturellen Aufbau abhängig, kann der überlagerte Regler R kontinuierlich oder diskontinuierlich arbeiten. Auch logische Verknüpfungen und Schrittfolgen sind möglich. Im eigentlichen Sinne der Regelungstechnik ist er damit im jeweiligen Anwendungsfall nicht immer als Regler zu bezeichnen, sondern nur die Gesamtstruktur.

Im einfachsten Anwendungsfall macht der Block R als reines Steuerglied in einer offenen Wirkungskette dabei nichts weiter, als schrittweise langsam und systematisch den Reglerausgang y_r von einer Stellgröße auf die nächste weiterzuschalten.

Der zweite Lösungsweg besteht darin, dass der Extremwertregler in seiner Struktur bereits so ausgelegt ist, dass er mehrere Stellgrößen zugleich beeinflusst. Aus der Literatur ist bisher nur ein Prinzip bekannt, das hier einzuordnen ist.^[3] Dieses Verfahren wird in ^[4] als Extremwertregler mit Synchrondetektor bezeichnet. Grundlegend beschrieben ist dieses Verfahren in ^[1].

Anwendungen

• Verbrennungsprozesse^[5][6][7]

• Strömungsprozesse^[8][9]

• Elektrotechnik^[10]

• Beschleunigertechnik^[3]

• Chemie^[11]

• Kältetechnik^[12]

Im Vergleich zur Gesamtmenge an Literatur über Regelungstechnik macht das Fachgebiet der Extremwertregelung nur einen verschwindend kleinen Anteil aus. Daraus müsste sich schlussfolgern lassen, dass auch der Anteil an Anwendungen entsprechend gering ist. Allerdings ist es wohl eher so, dass einerseits ein Teil der potentiellen Anwendungen mit Instrumenten der mathematischen Optimierung gelöst wurde oder andererseits unbewusst Verfahren der Extremwertregelung implementiert wurden, ohne dies explizit diesem Fachgebiet zuzuordnen, was wiederum eine negative Rückwirkung auf die Zahl der Veröffentlichungen hatte.

Literatur

Leider gibt es zumindest im deutsch- und englischsprachigen Raum keine Literatur, die das Fachgebiet umfassend abhandelt. Allerdings hat sich in den letzten Jahren offenbar das Verfahren durchgesetzt, dass auf einer Korrelation von Test- und Zielsignal basiert. Dieses wird von der theoretischen Seite und mit zahlreichen Anwendungsfällen und Literaturverweisen versehen in ^[1] beschrieben.

• Ariyur, Kartik B.; Krsti, Miroslav: Real-Time Optimization by Extremum-Seeking Control. 1. Auflage. Wiley, 2003, ISBN 978-0-471-46859-2
• Morossanow, I. S.: Relais-Extremwertregelungssysteme. Verlag Technik, Berlin, 1967
• Solodovnikov, W. W.: Nichtlineare und selbsteinstellende Systeme. Verlag Technik, Berlin, 1975
• Iwachnenko, A. G.: Technische Kybernetik. Einführung in die Grundlagen automatischer, adaptiver Systeme. 2. Aufl. Verlag Technik, Berlin, 1964

Einzelnachweise

1. ↑ ^{a b c} Ariyur, Kartik B.; Krsti, Miroslav: Real-Time Optimization by Extremum-Seeking Control. 1. Auflage. Wiley, 2003, ISBN 978-0-471-46859-2
2. ↑ Chunlei, Z.; Ordonez R.: Numerical optimization-based extremum seeking control with application to ABS design. vollständig veröffentlicht in IEEE transactions on automatic control, 2007, vol. 52, no3, pp. 454-467, ISSN 0018-9286
3. ↑ ^{a b} Herbrand, F.: Extremwertregler zur automatischen Strahlführung an Linearbeschleunigern für Ionen. Zeitschrift atp 8/2001
4. ↑ Schulze, K.-P. und Rehberg, K.-J.: Entwurf von adaptiven Systemen. Eine Darstellung für Ingenieure. Verlag Technik, Berlin 1988
5. ↑ Mehrskalen-asymptotische Verfahren zur Kontrolle thermoakustischer Prozesse in Brennkammern. TU Berlin
6. ↑ AIR-FUEL MIXTURE REGULATING SYSTEM IN AN INTERNAL COMBUSTION ENGINE Patent PCT/DE98/03708
7. ↑ Entwicklung eines echtzeitfähigen Indiziersystems. TU Darmstadt
8. ↑ Schulz, Jan: Aktive Geräuschminderung des Drehklangs axialer Turbomaschinen durch Strömungsbeeinflussung. Dissertation 2004, TU Berlin (PDF, 9MB)
9. ↑ Strömungsregelung stumpfer Körper. in Doktorandenkolloquium, Programm & Book of Abstracts. TU Berlin, S. 28ff (PDF 4MB)
10. ↑ Extremwertregler zur optimalen Arbeitspunkteinstellung regenerativer Energiekonverter (MPP-Regler). Patentanmeldung DE9217595U1
11. ↑ Martínez, E.: Extremum-seeking control of redox processes in wastewater chemical treatment plants. Beitrag zu 17th European Symposium on Computer Aided Process Engineering (PDF 300kB)
12. ↑ Yaoyu Li et al.: Extremum Seeking Control of a Tunable Thermoacoustic Cooler (PDF, 1,3MB) veröffentlicht auch in IEEE TRANSACTIONS ON CONTROL SYSTEMS TECHNOLOGY, VOL. 13, NO. 4, JULY 2005, pp. 527-538

Anmerkungen

1. ↑ ^{a b} Diese Tatsache ist durch die begriffliche Situation im englischen Sprachraum sehr verwirrend. Dort taucht der Begriff 'Adaptive extremum-seeking control' auf, aus dem allein nicht klar hervorgeht, ob es sich um einen reinen Extremwertregler oder einen Extremwertregler dessen Eigenschaften (Parameter) durch adaptive Verfahren beeinflusst werden handelt oder ob innerhalb eines Adaptiven Reglers ein Extremwertregler im Sinne eines Suchverfahrens zur Parameterschätzung für das Prozessmodell verwendet wird (bei Model Identification Adaptive Controllers) bzw. direkt den Parametern des Reglerblocks im Adaptiven Regler verändert (bei Model Reference Adaptive Controllers).
2. ↑ Theoretisch lässt sich hier auch ein Vektor denken, vergleichbar zu Vektoroptimierungsproblemen. Dies kann jedoch zu Problemen in der Art führen, dass entweder unbemerkt mehrere lokale Extrema entstehen oder die einzelnen Vektorelemente gegenseitig in Konkurrenz stehen. Da aber nicht der Prozess dafür zuständig ist, den optimalen Arbeitspunkt vorzugeben, sondern der Anwender, muss dieser letztlich in der Lage sein, aus den Messgrößen einen entsprechenden Zusammenhang herzustellen, der aus Sicht des Anwenders den optimalen Zustand des zu regelnden Systems widerspiegelt.
3. ↑ Diese hier dargestellte Bedingung gilt im Übrigen für alle Optimierungsverfahren, die mit der Bestimmung des Gradienten der Zielfunktion arbeiten. In der Literatur der Optimierungsverfahren spricht man bei dieser Zielgröße oft auch vom Güte- oder Qualitätswert. Teilweise wird dort in Anlehnung an Optimierungen im wirtschaftlichen Bereich auch der Begriff Kosten verwendet.