FPT

Die parametrisierte Algorithmik ist ein relativ junges Teilgebiet der theoretischen Informatik, in dem genauer untersucht wird, welche Instanzen von NP-vollständigen Problemen effizient zu lösen sind. Dabei wird untersucht, von welchen Faktoren (Parametern) die Laufzeit der Algorithmen im Wesentlichen abhängt. Zum Beispiel sind viele Graphen-Probleme schnell lösbar für Graphen mit kleiner Baumweite.

Formal ist ein Problem parametrisierbar (auch: fixed parameter tractable oder FPT), wenn ein Algorithmus existiert, der es mit einer Laufzeit aus 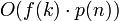$O(f(k)\cdot p(n))$ löst, wobei f eine beliebige Funktion, k der Parameter, p ein beliebiges Polynom und n die Eingabelänge (z. B. bei Graphenproblemen die Anzahl der Knoten) ist.

In der Praxis ist f oft eine unangenehme Funktion wie k^k, man geht im Allgemeinen aber davon aus, dass k sehr klein ist (weil dies bei Instanzen, die in der Praxis vorkommen, häufig der Fall ist) und n groß werden kann. Parametrisierte Algorithmen sind in der Praxis (wo k klein ist) auch für n=50–100 praktikabel, wogegen z. B. gewöhnliche Brute-Force Algorithmen mit Laufzeiten wie O(2ⁿ) schon ab etwa n=20 nicht mehr praktikabel sind.

Beschränkte Berechnungsbäume

Eine häufig benutzte Methode sind Berechnungsbäume, deren Höhe und Verzweigung durch Funktionen in k beschränkt sind. Die Verzweigung kann man häufig sogar durch Konstanten beschränken. Einen solchen Algorithmus kann man z. B. für das Knotenüberdeckungs-Problem benutzen, wobei der Parameter k die Größe einer minimalen Knotenüberdeckung ist.

Eine Methode wäre hier, eine beliebige, noch nicht überdeckte Kante e zu wählen und über die beiden zu e inzidenten Knoten zu verzweigen (in den beiden Zweigen des Berechnungsbaums wird je einer der Knoten in die Knotenüberdeckung aufgenommen). Die Verzweigung ist also 2 und da man maximal k Knoten wählt, ist die Höhe des Berechnungsbaums durch k beschränkt. Die Wahl einer noch nicht überdeckten Kante und die Aufnahme eines Knotens in die Knotenüberdeckung sind je in O(n) möglich, womit die Laufzeit insges. aus 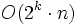$O(2^k\cdot n)$ ist.

Problemkern-Reduktion

Ein Problem ist genau dann parametrisierbar, wenn es dafür eine Problemkern-Reduktion gibt. Eine Problemkern-Reduktion verkleinert eine Instanz eines Problems auf eine Instanz, deren Größe durch eine Funktion in k beschränkt ist. 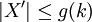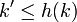Formal handelt es sich bei einer Problemkern-Reduktion um eine Funktion r, die eine Instanz X eines Problems und den Parameter k abbildet auf eine Instanz X' und einen Parameter k', wobei $|X'|\le g(k)$ und $k' \le h(k)$ für zwei Funktionen g, h.

Diese Methode lässt sich z. B. auf das Knotenüberdeckungsproblem anwenden: Wenn ein Knoten einen größeren Grad als k hat, muss er in einer minimalen Knotenüberdeckung enthalten sein, denn wenn ein Knoten v nicht enthalten ist, müssen alle seine Nachbarn enthalten sein (da alle zu v inzidenten Kanten überdeckt werden müssen), was aber mehr als k Knoten wären, obwohl k als Größe einer minimalen Knotenüberdeckung definiert war.

Nachdem auf diese Weise Knoten ausgewählt wurden, die definitiv in einer minimalen Knotenüberdeckung enthalten sein müssen, können noch maximal k² + k Knoten übrig sein (k Knoten für die Knotenüberdeckung und jeweils maximal k Nachbarn).

Interleaving

Die Interleaving Methode ist, vor jedem Rekursionsaufruf eine Problemkern-Reduktion durchzuführen. Im Allgemeinen wird die Laufzeit dadurch stark reduziert, von 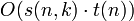$O(s(n,k)\cdot t(n))$ auf O(s(n,k) + t(n) + r(n)), wobei s(n,k) die Anzahl der Knoten im Berechnungsbaum ist, t(n) die Laufzeit der Expansion eines Knotens im Berechnungsbaum (die Generierung der Nachfolger) und r(n) die Laufzeit der Problemkernreduktion ist.

Color-Coding

Eine weitere Methode ist das Color-Coding, bei dem man die n Objekte in der Probleminstanz mit k Farben „färbt“. Wenn eine Lösung aus k Objekten aus der Instanz besteht, kann sie häufig schnell gefunden werden, wenn diese k Objekte unterschiedlich gefärbt sind. Man sagt dann, dass die Lösung farbenfroh (engl. colorful) ist. Da es perfekte Hash-Funktionen gibt, müssen höchstens 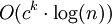$O(c^k\cdot \log(n))$ verschiedene Färbungen probiert werden, bis eine Lösung farbenfroh ist, wobei c eine Konstante ist.

Mit dieser Methode ist z. B. die Suche in einem Graphen nach einem Weg der Länge k parametrisierbar. Sind die Knoten auf einem Weg der Länge k unterschiedlich gefärbt, dann können die Farbklassen auf k! Arten angeordnet werden, alle Kanten entfernt werden, die zwischen nicht-benachbarten Farbklassen verlaufen, woraufhin z. B. mit dem Algorithmus von Floyd und Warshall in O(n³) geprüft werden kann, ob es noch einen Weg von einem Knoten der ersten Farbklasse zu einem Knoten der letzten Farbklasse gibt (falls es einen gibt, hat er mindestens Länge k). Die Laufzeit dieses Algorithmus ist in 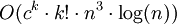$O(c^k\cdot k! \cdot n^3 \cdot \log(n))$, also ist es ein FPT Algorithmus.

Courcelles Theorem

Courcelles Theorem besagt, dass jedes Graphenproblem, welches durch eine erweiterte MS₂-logische Formel beschrieben werden kann, parametrisierbar ist mit der Baumweite als Parameter. Eine erweiterte MS₂-logische Formel ist dabei eine logische Formel mit Existenz- und Allquantor, die Mengen von Knoten oder Kanten quantifizieren können, erweitert um einen min und einen max Quantor.

Formeln aus erweiterter MS₂-Logik für folgende Probleme auf einem Graphen G=(V,E) sind z. B.:

1. Minimale Knotenüberdeckung: $\min U\subseteq V: \forall e \in E: \exists v \in U: \operatorname{inc}(v,e)$
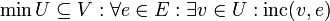
2. Minimale dominierende Knotenmenge: $\min U\subseteq V: \forall v \in V: (v \in U \vee \exists v' \in U: \operatorname{adj}(v,v'))$
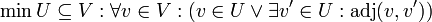
3. Maximale Clique: $\max U\subseteq V: \forall v,v' \in U: \operatorname{adj}(v,v')$

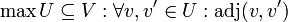
Literatur

• Rod Downey, M. Fellows: Parameterized complexity. Springer 1999, ISBN 0-387-94883-X

• Flum, J., Grohe, M.: Parameterized Complexity Theory. Springer 2006, ISBN 978-3-540-29952-3

• Rolf Niedermeier: Invitation to Fixed-Parameter Algorithms. Oxford University Press 2006, ISBN 0-19-856607-7