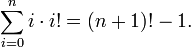Faktorielles Stellenwertsystem

In der Kombinatorik wird das fakultätsbasierte Zahlensystem verwendet, um einen eindeutigen Index für Permutationen zu erzeugen.

Definition

Das fakultätsbasierte Zahlensystem ist das Zahlensystem, das die ersten Fakultäten als Grundzahlen hat.

Stelle:	7	6	5	4	3	2	1	0
Stellenwert:	7!	6!	5!	4!	3!	2!	1!	0!
in Dezimaldarstellung:	5040	720	120	24	6	2	1	1

In diesem Zahlensystem ist die Stelle ganz rechts immer 0, die zweite Stelle von rechts 0 oder 1, die dritte 0, 1 oder 2 usw. Es gibt außerdem eine Variante des fakultätsbasierten Zahlensystems, bei dem die rechte Zahl weggelassen wird, da sie immer 0 ist.

Beispiel

Die Zahl 35 würde man in diesem Zahlensystem folgendermaßen schreiben.

35 = 1 * 4! + 1 * 3! + 2 * 2! + 1 * 1! + 0 * 0! = 1₄1₃2₂1₁0₀

Eigenschaften

Die Summe der aufeinanderfolgenden Fakultäten, multipliziert mit ihrem Index, ist immer die nächste Fakultät minus eins:

$\sum_{i=0}^{n} {i\cdot i!} = {(n+1)!} - 1.$

Daher kann jede Zahl in diesem Zahlensystem dargestellt werden und diese Darstellung ist eindeutig, d.h. keine Zahl kann auf mehr als eine Art dargestellt werden.

Allerdings benötigt man dafür eine unendliche Anzahl an Zeichen. Die einfache Verknüpfung von dezimalen Ziffern wäre mehrdeutig für Zahlen mit einer "Ziffer", die größer ist als 9 ist. Das kleinste Beispiel hierfür ist die Zahl 10×10!, ausgeschrieben 10₁₀0₉0₈0₇0₆0₅0₄0₃0₂0₁0₀ wobei 11! 1₁₁0₁₀0₉0₈0₇0₆0₅0₄0₃0₂0₁0₀ ist. Daher reicht ein einzelnes Subskript (wie im Dezimalsystem) für Zahlen mit mehr als 10 Stellen nicht aus.

Anwendung

Das fakultätsbasierte Zahlensystem wird benutzt, um eine kanonische Zuordnung zwischen den ganzen Zahlen 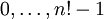$0, \dots, n!-1$ (bzw. den äquivalenten Zahlen mit n Stellen im fakultätsbasierten Zahlensystem) und Permutationen von n Elementen in lexikographischer Reihenfolge, wenn die ganzen Zahlen bezüglich dieses Zahlensystems dargestellt werden. Diese Zuordnung wird Lehmer-Code oder Lucas-Lehmer-Code genannt. Zum Beispiel ergibt sich mit n = 3 folgende Zuordnung:

dezimal	fakultätsbasiert	Permutation
010	020100	(0,1,2)
110	021100	(0,2,1)
210	120100	(1,0,2)
310	121100	(1,2,0)
410	220100	(2,0,1)
510	221100	(2,1,0)

dabei wählt die linke Ziffer 0, 1 oder 2 sich selbst als Permutationsziffer aus der sortierten Liste (0,1,2) aus und entfernt sich aus der Liste. Es entsteht eine kürzere Liste, bei der die erste Permutationsziffer fehlt. Mit der zweite Ziffer wird die zweite Permutationsziffer ausgewählt. Dabei beginnt das Abzählen mit 0. Das Element wird aus der Liste wieder entfernt. Die dritte Stelle ist "0". Da die Liste nur noch ein Element enthält, wird dieses als letzte Permutationsziffer ausgewählt.

Dieser Vorgang wird mit einem längerem Beispiel deutlicher. Im folgenden werden mit den Ziffern aus dem fakultätsbasierten Zahlensystem 4₆0₅4₄1₃0₂0₁0₀ die Ziffern aus der Permutation (4,0,6,2,1,3,5) erzeugt.

                                 46054413020100 → (4,0,6,2,1,3,5)
Fakultätsbasiert: 46         05                       44       13         02         01       00
                  |          |                        |        |          |          |        |
         (0,1,2,3,4,5,6) → (0,1,2,3,5,6) → (1,2,3,5,6) → (1,2,3,5) → (1,3,5) → (3,5) → (5)
                  |          |                        |        |          |          |        |
Permutation:     (4,         0,                       6,       2,         1,         3,       5)

Der natürliche Index für das direkte Gruppenprodukt von zwei Permutationsgruppen ist einfach die Konkatenation.

dezimal	fakultätsbasiert	Permutationspaar
010	020100020100	((0,1,2),(0,1,2))
110	020100021100	((0,1,2),(0,2,1))
...
510	020100221100	((0,1,2),(2,1,0))
610	021100020100	((0,2,1),(0,1,2))
710	021100021100	((0,2,1),(0,2,1))
...
2210	121100220100	((1,2,0),(2,0,1))
...
3410	221100220100	((2,1,0),(2,0,1))
3510	221100221100	((2,1,0),(2,1,0))

Literatur

• Donald Knuth. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89684-2. Pages 65–66 (englisch).

Weblinks

• Laisant, C.- A., Sur la numération factorielle, application aux permutations. Bulletin de la Société Mathématique de France, 16 (1888), p. 176-183 (französisch)
• "Using Permutations in .NET for Improved Systems Security", by Dr. James McCaffrey. Implementation of factoradics in C# source code
• Peter Cameron's Home Page McCaffrey acknowledges Cameron as having first suggested to him using factoradics to index permutations (englisch).
• "A permutation representation that knows what 'Eulerian' means", by Roberto Mantaci and Fanja Rakotondrajao. (PDF) Description and references for Lehmer codes (englisch)
• A Lehmer code calculator Note that their permutation digits start from 1, so mentally reduce all permutation digits by one to get results equivalent to the ones on this page (englisch).