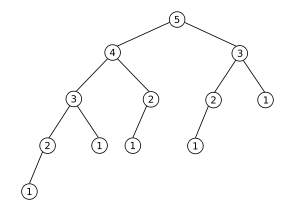
Fibonacci-Baum

Ein Fibonacci-Baum ist eine Datenstruktur in der Informatik. Er stellt einen Spezialfall eines AVL-Baums dar. Der Name deutet an, dass Fibonacci-Bäume analog zu den Fibonacci-Zahlen rekursiv definiert sind.

Entfernt man einen beliebigen Knoten eines Fibonacci-Baums, so entsteht bei den Stufen ≥ 3 ein Baum, der nicht mehr Fibonacci-Baum ist. Im Beispiel unten ist er auch nicht mehr AVL-Baum, wenn z. B. eine 1, die nicht die linkeste ist, entfernt wird.

Eine Art „Basis des Logarithmus“ ist wie bei den Fibonacci-Zahlen die Zahl  $\Phi := \tfrac{1+\sqrt 5}{2} \approx 1{,}618034$  des goldenen Schnittes. Ideal wäre für einen Binärbaum natürlich die Basis 2, das Aufrechterhalten schärferer Balancekriterien, z. B. der Höhenausgewogenheit beim vollständig balancierten Binärbaum, ist aber nach Modifikationen des Baums so aufwändig, dass im Mittel die Gesamtkosten solcher Bäume höher werden, es sei denn die Anwendung ist ganz extrem vom Suchen dominiert. Das AVL-Kriterium erscheint als attraktiver Kompromiss.

Fibonacci-Baum der Stufe 5

Rekursive Definition

Die rekursive Definition erfolgt in der Art:

• Der Fibonacci-Baum der Stufe 0 ist der leere Baum.
• Der Fibonacci-Baum der Stufe 1 ist ein Baum, der nur aus einem Knoten besteht.
• Ein Fibonacci-Baum der Stufe h (mit h ≥ 2) besteht aus einer Wurzel, deren linker Sohn ein Fibonacci-Baum der Stufe h − 1 und deren rechter Sohn ein Fibonacci-Baum der Stufe h − 2 ist.

Eigenschaften

• Alle inneren Knoten haben den Balance-Wert –1.
• Der Fibonacci-Baum der Stufe h (mit h ≥ 0) hat die Höhe h.

• Ist n_h die Anzahl der Knoten des Fibonacci-Baums der Stufe h, dann gilt

  n₀ = 0

  n₁ = 1

  n_h = 1 + n_{h − 1} + n_{h − 2} (h ≥ 2)

• Ist b_h die Anzahl der Blattknoten des Fibonacci-Baums der Stufe h, dann gilt

  b₀ = 0

  b₁ = 1

  b_h = b_{h − 1} + b_{h − 2} (h ≥ 2)

• Ist e_h die Anzahl der Einfügepunkte (Halb-Blätter; 1 Blatt = 2 Halb-Blätter) des Fibonacci-Baums der Stufe h, dann gilt

  e₀ = 1

  e₁ = 2

  e_h = e_{h − 1} + e_{h − 2} (h ≥ 2)

• Mit Hilfe der Bezeichnung f_h für die h-te Fibonacci-Zahl lassen sich diese Größen auch so ausdrücken:

  n_h = f_{h + 2} − 1

  b_h = f_h

  e_h = f_{h + 2} = n_h + 1

(Für jeden gerichteten Binärbaum gilt e = n + 1.)

• Zu einer gegebenen Höhe entspricht ein Fibonacci-Baum einem AVL-Baum mit minimaler Knotenanzahl, er ist also am schlechtesten balanciert.

• Nach der Formel von Moivre-Binet ist die Anzahl der Knoten

$n = -1+f_{h+2} = -1+\frac{1}{\sqrt{5}} \left[ \left(\frac{1+\sqrt 5}{2}\right)^{h+2} - \left(\frac{1-\sqrt 5}{2}\right)^{h+2} \right] \geqq \quad \frac{\Phi^{h+2}}{\sqrt{5}} - 2$,

wo  h  die Höhe des Fibonacci-Baums ist.

Damit lässt sich die Höhe in Abhängigkeit von der Knotenanzahl abschätzen zu

$h \leqq a \log_2 (n + 2) + b$  mit  $a:=\frac{1}{\log_2 \Phi} \approx 1{,}440420$  und  $b:=\frac{a}{2} \log_2 5 -2 \approx -0{,}327724$.

Suchtiefe

Die Suchtiefe eines Knotens ist die Anzahl der Bögen von der Wurzel bis zum Knoten. Bei einem binären Suchbaum entspricht die Anzahl der erforderlichen Vergleiche der Suchtiefe +1.

Die Summe $s_h := \sum_{k \in t} T(k)$ der Suchtiefen T(k) über alle Knoten k des Fibonacci-Baums t der Stufe h lässt sich wie folgt rekursiv berechnen:

s₀ = 0     (leerer Baum)

s₁ = 1     (Wurzel)

s_h = (1) + (s_{h − 1} + n_{h − 1}) + (s_{h − 2} + n_{h − 2})     (neue Wurzel) + [(linker Sohn) + (rechter Sohn)] jeweils eine Ebene tiefer

$\quad = n_{h}+s_{h-1}+s_{h-2} = f_{h+2}-1+s_{h-1}+s_{h-2}$   (für h = 2,3,...).

Dies wird befriedigt durch

$s_{h} = \left[ h \left( 3 f_{h+2} + f_{h+1} \right) - 2 f_{h+2} - 3 f_{h+1} + 5 \right] / 5$.

Beweis:

f_{h + 2} − 1 + s_{h − 1} + s_{h − 2}

$\quad = f_{h+2}-1 + \left[ (h-1) \left( 3 f_{h+1} + f_{h} \right) - 2 f_{h+1} - 3 f_{h}+5 + (h-2) \left( 3 f_{h} + f_{h-1} \right) - 2 f_{h} - 3 f_{h-1}+5 \right] / 5$

$\quad = \left[ 5 f_{h+2} + h \left( 3 f_{h+1} + f_{h} \right) - 3 f_{h+1} - f_{h} - 2 f_{h+1} - 5 f_{h} + h \left( 3 f_{h} + f_{h-1} \right) - 6 f_{h} - 2 f_{h-1} - 3 f_{h-1} + 5 \right] / 5$

$\quad = \left[ h \left( 3 f_{h+1} + 4 f_{h} + f_{h-1} \right) + 5 f_{h+2} - 5 f_{h+1} - 12 f_{h} - 5 f_{h-1} + 5 \right] / 5$

$\quad = \left[ h \left( 3 f_{h+1} + 4 f_{h} + f_{h+1} - f_{h} \right) + 5 f_{h+2} - 5 f_{h+1} - 12 f_{h} - 5 f_{h+1} + 5 f_{h} + 5 \right] / 5$

$\quad = \left[ h \left( 4 f_{h+1} + 3 f_{h} \right) + 5 f_{h+2} - 10 f_{h+1} - 7 f_{h} + 5 \right] / 5$

$\quad = \left[ h \left( 4 f_{h+1} + 3 f_{h+2} - 3 f_{h+1}\right) + 5 f_{h+2} - 10 f_{h+1} - 7 f_{h+2} + 7 f_{h+1} + 5 \right] / 5$

$\quad = \left[ h \left( 3 f_{h+2} + f_{h+1}\right) - 2 f_{h+2} - 3 f_{h+1} + 5 \right] / 5$.  ■

Vermöge der Formel von Moivre-Binet lässt sich hieraus über die mittlere Pfadlänge (unter der Annahme von Einheits-Zugriffswahrscheinlichkeiten) $\bar P_{h} := s_{h} / n_{h}$ der Limes der Effizienz $\varphi :=\bar P_{h} / \log_2{n_{h}}$   für   $h \to \infty$   ableiten zu:

$\varphi \to h ( 3 \Phi^{h+2} + \Phi^{h+1} ) / 5 / \Phi^{h+2} / \log_2{n_{h}}$

$\quad \to h ( 3 + \Phi^{-1} ) / 5 / \log_2{f_{h+2}}$

$\quad \to h ( 3 + \Phi - 1 ) / 5 / (h+2) / \log_2{\Phi}$

$\quad \to ( 2 + \Phi ) / 5 / \log_2{\Phi} = ( 5/2 + \sqrt{5}/2 ) / 5 / \log_2{\Phi} = \Phi / \sqrt{5} / \log_2{\Phi} \approx 1{,}042298$.

Andere dünnste AVL-Bäume

Vertauscht man an einem Knoten den linken mit dem rechten Sohn, entsteht wieder ein dünnster AVL-Baum. Damit ergibt sich für die Anzahl a_h dünnster AVL-Bäume der Höhe h

a₀ = 1

a₁ = 1

a_h = (a_h–1 · a_h–2)            · 2                               (für h ≥ 2)

[nämlich für die Höhen

(h–1 links & h–2 rechts) + umgekehrt].

Das ist in geschlossener Form

$a_h = 2^{f_{h+1}-1}$, welches sich für   $h \to \infty$ der Funktion $2^{\Phi^{h+c}-1}$ mit $c := 1-\tfrac{\log_{\Phi}5}2 \approx -0{,}672276$ annähert.

Die Anzahl A_h aller AVL-Bäume der Höhe h lässt sich wie folgt berechnen:^[1]

A₀ = 1

A₁ = 1

A_h = (A_h–1 · A_h–2)           · 2              +         (A_h–1 · A_h–1)                       (für h ≥ 2)

[nämlich für die Höhen

(h–1 links & h–2 rechts) + umgekehrt + (h–1 links & h–1 rechts)].

Es handelt sich um die Folge A029758 in OEIS, die sich für   $h \to \infty$ der Funktion

$k^{2^h} = 2^{2^{h+C}}$ mit $k := k_{\mathsf{A029758}} \approx 1{,}436873$ oder $C := \log_2{\log_2{k}} \approx -0{,}935305$ annähert.^[2]

Beide Folgen sind doppelexponentiell, allerdings mit unterschiedlichen Exponenten – mit dem Ergebnis, dass die dünnsten Bäume mit wachsender Baumhöhe anteilig rasch (doppelexponentiell) selten werden.

Anteil der unausgewogenen Knoten

Eine etwas differenziertere Rekursion gestattet Einblick in die inneren Asymmetrien der AVL-Bäume. Sei dazu U_h,u,g die Anzahl der AVL-Bäume der Höhe h mit u unausgewogenen (rechts- oder linkslastigen) und g ausgewogenen Knoten mit gleich hohen Söhnen (ohne die Blätter). Dann ist nach Überlegungen analog zu oben

U_0,0,0 = 1

U_1,0,0 = 1

$U_{h,u,g}=\sum_{\upsilon,\gamma}(U_{h-2,\upsilon,\gamma}\cdot U_{h-1,u-1-\upsilon,g-\gamma}\cdot 2 +U_{h-1,\upsilon,\gamma}\cdot U_{h-1,u-\upsilon,g-1-\gamma})$,

denn bei den ungleich hohen Söhnen kommt ein u-Knoten hinzu und bei den gleich hohen Söhnen ein g-Knoten. Für die Anzahl der unausgewogenen Knoten über alle AVL-Bäume der Höhe h ergibt sich

$U_h:=\sum_{u,g}(U_{h,u,g}\cdot u)$

und für die Anzahl der ausgewogenen Knoten minus Blätter

$G_h:=\sum_{u,g}(U_{h,u,g}\cdot g)$.

Der Anteil der unausgewogenen Knoten an allen Knoten minus Blättern über alle AVL-Bäume der Höhe h ist dann

u_h := U_h/(U_h+G_h).

Die Anzahl aller AVL-Bäume der Höhe h ist übrigens

Ah: =	∑	Uh,u,g
	u,g

. Es ist dasselbe A_h wie oben.

Mittlere Verlängerung der Pfadlänge

Nach derselben Methode lässt sich eine mittlere Suchtiefe berechnen. Sei dazu P_h,n,p die Anzahl der AVL-Bäume der Höhe h mit n Knoten und der Pfadlängensumme p. Dann ist

P_0,0,0 = 1

P_1,1,1 = 1

$P_{h,n,p}=\sum_{\nu,\pi}(P_{h-2,\nu,\pi}\cdot P_{h-1,n-1-\nu,p-n-\pi}\cdot 2+P_{h-1,\nu,\pi}\cdot P_{h-1,n-1-\nu,p-n-\pi})$,

denn bei der rekursiven Zusammensetzung zweier Bäume erhöht sich die Knotenzahl von

n_links und n_rechts      auf      n_links+n_rechts+1   =: n

und die Pfadlängensumme von

p_links und p_rechts      auf      p_links+p_rechts+n.

Die Anzahl aller AVL-Bäume der Höhe h ist

Ah: =	∑	Ph,n,p
	n,p

. Es ist dasselbe A_h wie oben.

Bei einem Baum mit Knotenzahl n und Pfadlängensumme p ist die mittlere Pfadlänge bei erwartetem Suchergebnis „gefunden“ p/n und die mittlere Pfadlänge bei erwartetem Suchergebnis „nicht gefunden“ (p+n)/(n+1). Letztere Pfadlänge sei der idealen Pfadlänge log ₂(n + 1) für den Fall „nicht gefunden“ gegenübergestellt: Die Verlängerung der Pfadlänge gegenüber der idealen Pfadlänge ist $V_{n,p}:=\tfrac{p+n}{(n+1)log_2{(n+1)}}$. Wir mitteln über alle AVL-Bäume der Höhe h

$v_h:=\sum_{n,p}(P_{h,n,p}\cdot V_{n,p})/A_h$.

h	Ah	Uh	Gh	uh	nh,min	nh,max	nh,mittel	vh	1+0,08·uh2
2	3	2	1	0,66667	2	3	2,33333	1,03436	1,036
3	15	22	17	0,56410	4	7	5,13333	1,02634	1,025
4	315	942	867	0,52073	7	15	10,46667	1,02605	1,022
5	108675	645030	682155	0,48601	12	31	21,46957	1,02277	1,019
6	11878720875	140876848350	160694844975	0,46714	20	63	43,87571	1,01940	1,017
7	141106591 466142946875	3346922044 284331668750	3958853561 927235759375	0,45812	33	127	88,75101	1,01669	1,017
8	19911 070158545297 149037891328 865229296875	944545 523266338303 258999007810 250235468750	1137151 734768897989 421320315727 595038984375	0,45374	54	255	178,50203	1,01457	1,016

Die in der Tabelle angegebenen Werte für u und v korrelieren gut mit den recht groben Abschätzungen im Artikel AVL-Baum. Dennoch müssen sie nicht mit Ergebnissen „zufälliger“ AVL-Bäume übereinstimmen, da hier jeder AVL-Baum als gleich wahrscheinlich angenommen wird, wogegen es in der Praxis AVL-Bäume geben mag, die „bevorzugt“ sind, d. h. von anderen Bäumen bei Modifikationen häufiger erreicht werden. Z. B. spricht viel dafür, dass unter den 3 Bäumen der Höhe 2 der ausgewogene Baum häufiger vorkommt als jeder der beiden anderen (mit Knotenzahl 2), da er der einzige AVL-Baum mit der Knotenzahl 3 ist.

Siehe auch

• Fibonacci-Folge
• Fibonacci-Heap

Literatur

1. ↑ Donald E. Knuth: The Art of Computer Programming, Volume 3, Sorting and Searching. Addison-Wesley, 1998, ISBN 0-201-89685-0, 6.2.3 Balanced Trees.
2. ↑ A. V. Aho and N. J. A. Sloane: Some Doubly Exponential Sequences. In: Fib. Quart., 11, Bell Laboratories Murray Hill, New Jersey. 1970, S. 429-437.