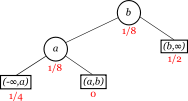
Gewichteter binärer Suchbaum

Ein binärer Suchbaum mit 2 Knoten und Gewichts-Angaben (rot)

In der Informatik ist ein gewichteter binärer Suchbaum eine Ausprägung der abstrakten Datenstruktur binärer Suchbaum, bei der jedem Knoten neben Schlüssel und anderen Daten ein Gewicht (Zugriffswahrscheinlichkeit) zukommt. (Der Vollständigkeit halber kommt ein solches auch seinen Nachbarintervallen zu.)

Zu optimieren ist die gewichtete Pfadlänge des Baums.

Das Gewicht ist an den Schlüssel gebunden, somit macht das Zulassen von mehreren Objekten („Duplikaten“) mit gleichem Schlüssel keinen Sinn.

Sind Gewichte überhaupt nicht bekannt oder sind sie untereinander praktisch gleich, dann sind höhen-balancierte Bäume eine gute Wahl. Ein Beispiel ist der AVL-Baum, der als optimiert auf die gewichtete Pfadlänge bei Einheitsgewichten angesehen werden kann.

Beispiele

Ist der Baum statisch, spielen also Einfüge- oder Entfernoperationen keine Rolle, so bietet sich der Bellman-Algorithmus an, der einen optimalen gewichteten binären Suchbaum konstruiert. Seine Effizienz ist auch dann gegeben, wenn die Gewichte nur ungefähr bekannt sind.

Geometrische Verteilung

Bei der geometrischen Gewichtsverteilung p_i = (1 − q)qⁱ  für i = 0,1,...  mit 0 < q < 1  haben wir  $\sum_{i \geqq 0}p_i = 1$ und die gewichtete Pfadlänge  $\sum_{i \geqq 0}(i+1)p_i = 1/(1-q)$ ist konstant und unabhängig von der Anzahl der Knoten. Allerdings gibt es dann sehr seltene Suchanfragen, die in nur linearer Zeit beantwortet werden.

Natürliche Vokabulare

Im Englischen ist die Wahrscheinlichkeit für das Vorkommen des i-t häufigsten Wortes ungefähr

$\alpha_i \approx i^{-1{,}12} / \sum_{i \geqq 1}i^{-1{,}12}$.

Die gewichtete Pfadlänge eines optimalen binären Suchbaums für alle englischen Wörter ergibt sich zu ungefähr 10,2.

Dynamische Gewichte

Sind Einfüge- oder Entfernoperationen wichtig, so sind im Prinzip auch die Gewichte zu pflegen. Im Grenzfall sogar beim Aufsuchen, da sich hierbei zumindest die Zugriffsstatistik ändert.

Mehlhorn beschreibt „Nahezu optimale binäre Suchbäume“. Ferner führt er BB[α]-Bäume ein, die sich ebenfalls nicht weit vom Optimum entfernen.

Bei den Splay-Bäumen werden trotz völlig anderer Vorgehensweise ebenfalls die am häufigsten angesprochenen Knoten in die Nähe der Wurzel gespült.

Zugriffsverteilung und gewichtete Pfadlänge

Sei $S = \left\{ k_1 < k_2 < ... < k_n \right\}$  eine Schlüsselmenge aus einem total geordneten Reservoir R von Schlüsseln, sei p_i  resp. q_j  die Wahrscheinlichkeit, dass auf das Element $x \in R$  zugegriffen wird, wobei x = k_i  resp. k_j < x < k_{j + 1}  für $1 \leqq i \leqq n$  resp. $0 \leqq j \leqq n$. (Dabei sind $k_0 := -\infty$  und $k_{n+1} := +\infty$  zusätzliche nicht zu R gehörende Elemente mit der üblichen Bedeutung.) Das (2n + 1)-Tupel ζ: = (q₀,p₁,q₁,...,p_n,q_n)  heißt Zugriffsverteilung für die Menge S, wenn alle $p_i, q_j \geqq 0$  und $\sum p_i + \sum q_j = 1$.

Sei nun T  ein Suchbaum für die Menge S mit obiger Zugriffsverteilung ζ, sei $a_i^T$  die Tiefe des Knotens k_i  und $b_j^T$  die Tiefe des Blattes (k_j,k_{j + 1}) (s. Abb.). Wir betrachten die Suche nach einem Element $x \in R$. Wenn x = k_i, dann vergleichen wir x  mit $a_i^T+1$  Elementen im Baum. Wenn k_j < x < k_{j + 1}, dann vergleichen wir x  mit $b_j^T$ Elementen im Baum. Also ist

$P^T := \sum_{i=1}^n p_i (a_i^T+1) + \sum_{j=0}^n q_j b_j^T$  die (mit der Zugriffsverteilung ζ) gewichtete Pfadlänge des Baumes T.

Siehe auch

• Binärer Suchbaum
• Bellman-Algorithmus (Konstruktion des optimalen gewichteten binären Suchbaums)
• Splay-Baum

Literatur

• Kurt Mehlhorn Datenstrukturen und effiziente Algorithmen Teubner Stuttgart 1988, ISBN 3-519-12255-3.