Fixpunktsatz von Kakutani
- Fixpunktsatz von Kakutani
-
Eine Korrespondenz von einer Menge A in eine Menge B ist eine Abbildung φ von A in die Potenzmenge von B. Damit handelt es sich um eine Präzisierung des in der älteren mathematischen Literatur häufiger anzutreffenden Begriffs der mehrwertigen Funktion.
Korrespondenzen als Relation
Eine Korrespondenz φ von A nach B kann mit der Relation 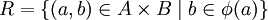 identifiziert werden, denn aus der Relation
identifiziert werden, denn aus der Relation 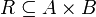 erhält man durch die Definition
erhält man durch die Definition 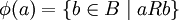 wieder die Korrespondenz zurück.
wieder die Korrespondenz zurück.
Eigenschaften von Korrespondenzen
Sind A und B topologische Räume, so lassen sich interessante Eigenschaften von Korrespondenzen φ zwischen A und B definieren.
Man nennt φ abgeschlossen (offen), wenn die zugehörige Relation im Produktraum abgeschlossen (offen) ist.
Ein Fixpunkt einer Korrespondenz φ von A nach A ist ein Punkt 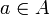 mit
mit 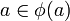 .
.
Der folgende, nicht-konstruktive Existenzsatz von Shizuo Kakutani sichert die Existenz von Fixpunkten.
Fixpunktsatz von Kakutani
Sei 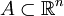 nicht leer, konvex und kompakt, und sei φ eine abgeschlossene Korrespondenz von A nach A derart, dass φ(a) für jedes a konvex und nicht leer ist. Dann besitzt φ einen Fixpunkt.
nicht leer, konvex und kompakt, und sei φ eine abgeschlossene Korrespondenz von A nach A derart, dass φ(a) für jedes a konvex und nicht leer ist. Dann besitzt φ einen Fixpunkt.
Anwendungen
Dieser Fixpunktsatz verallgemeinert den brouwerschen Fixpunktsatz, denn eine Abbildung 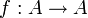 kann man als Korrespondenz φ mit φ(a) = {f(a)} auffassen, und ein Fixpunkt von φ ist ein Fixpunkt von f.
kann man als Korrespondenz φ mit φ(a) = {f(a)} auffassen, und ein Fixpunkt von φ ist ein Fixpunkt von f.
In der mathematischen Wirtschaftstheorie führt dieser Satz zu interessanten Existenzsätzen über Gleichgewichtspreise. In der mathematischen Spieltheorie hat John Forbes Nash diesen Satz verwendet, um die Existenz von Gleichgewichtspunkten in gewissen kooperativen Zweipersonenspielen zu zeigen (siehe Nash-Gleichgewicht).
Literatur
- Heinz König, Michael Neumann: Mathematische Wirtschaftstheorie. Verlag Anton Hain Meisenheim GmbH (1986)
- Burkhard Rauhut, Norbert Schmitz, Ernst-Wilhelm Zachow: Eine Einführung in die mathematische Theorie strategischer Spiele. Teubner Studienbücher (1979)
- Heuser: Lehrbuch der Analysis - Teil 2. 5-te Auflage, Teubner 1990, ISBN 3-519-42222-0, S.609
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Fixpunktsatz — Ein Fixpunktsatz ist in der Mathematik ein Satz, der einem unter gewissen Voraussetzungen die Existenz von Fixpunkten einer Abbildung garantiert. Das heißt der Satz garantiert die Existenz eines Punktes mit . Inhaltsverzeichnis 1 Überblick … Deutsch Wikipedia
Shizuo Kakutani — (1970) Shizuo Kakutani (jap. 角谷 静夫, Kakutani Shizuo; * 28. August 1911 in Ōsaka; † 17. August 2004 in New Haven, Connecticut) war ein japanisch amerikanischer Mathematiker. Kakutani besuchte die Universität Tohoku, dort war Tatsujiro Shimizu sein … Deutsch Wikipedia
Korrespondenz (Mathematik) — Eine Korrespondenz von einer Menge A in eine Menge B ist eine Abbildung ϕ von A in die Potenzmenge von B. Damit handelt es sich um eine Präzisierung des in der älteren mathematischen Literatur häufiger anzutreffenden Begriffs der mehrwertigen… … Deutsch Wikipedia
Liste mathematischer Sätze — Inhaltsverzeichnis A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A Satz von Abel Ruffini: eine allgemeine Polynomgleichung vom … Deutsch Wikipedia
Nash-Equilibrium — Das Nash Gleichgewicht, teils auch (wie im Englischen) Nash Equilibrium genannt, ist ein zentraler Begriff der mathematischen Spieltheorie. Es beschreibt in nicht kooperativen Spielen einen Zustand eines strategischen Gleichgewichts, von dem… … Deutsch Wikipedia
Nash-Program — Das Nash Gleichgewicht, teils auch (wie im Englischen) Nash Equilibrium genannt, ist ein zentraler Begriff der mathematischen Spieltheorie. Es beschreibt in nicht kooperativen Spielen einen Zustand eines strategischen Gleichgewichts, von dem… … Deutsch Wikipedia
Nash Equilibrium — Das Nash Gleichgewicht, teils auch (wie im Englischen) Nash Equilibrium genannt, ist ein zentraler Begriff der mathematischen Spieltheorie. Es beschreibt in nicht kooperativen Spielen einen Zustand eines strategischen Gleichgewichts, von dem… … Deutsch Wikipedia
Nash Gleichgewicht — Das Nash Gleichgewicht, teils auch (wie im Englischen) Nash Equilibrium genannt, ist ein zentraler Begriff der mathematischen Spieltheorie. Es beschreibt in nicht kooperativen Spielen einen Zustand eines strategischen Gleichgewichts, von dem… … Deutsch Wikipedia
Nashgleichgewicht — Das Nash Gleichgewicht, teils auch (wie im Englischen) Nash Equilibrium genannt, ist ein zentraler Begriff der mathematischen Spieltheorie. Es beschreibt in nicht kooperativen Spielen einen Zustand eines strategischen Gleichgewichts, von dem… … Deutsch Wikipedia
Théorème du point fixe de Brouwer — En 1886 Henri Poincaré démontre un résultat équivalent au théorème du point fixe de Brouwer. L énoncé exact est prouvé pour la dimension trois par Piers Bohl pour la première fois en 1904, puis par Jacques Hadamard dans le cas général en 1910.… … Wikipédia en Français
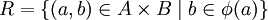 identifiziert werden, denn aus der Relation
identifiziert werden, denn aus der Relation 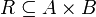 erhält man durch die Definition
erhält man durch die Definition 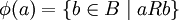 wieder die Korrespondenz zurück.
wieder die Korrespondenz zurück.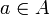 mit
mit 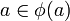 .
.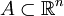 nicht leer, konvex und kompakt, und sei φ eine abgeschlossene Korrespondenz von A nach A derart, dass φ(a) für jedes a konvex und nicht leer ist. Dann besitzt φ einen Fixpunkt.
nicht leer, konvex und kompakt, und sei φ eine abgeschlossene Korrespondenz von A nach A derart, dass φ(a) für jedes a konvex und nicht leer ist. Dann besitzt φ einen Fixpunkt.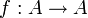 kann man als Korrespondenz φ mit φ(a) = {f(a)} auffassen, und ein Fixpunkt von φ ist ein Fixpunkt von f.
kann man als Korrespondenz φ mit φ(a) = {f(a)} auffassen, und ein Fixpunkt von φ ist ein Fixpunkt von f.