Ford-Kreis

Ford-Kreise der Farey-Reihe der fünften Ordnung

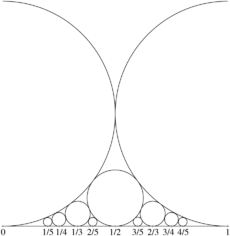
Die Ford-Kreise sind Kreise in der reellen Ebene, je einer für jede rationale Zahl und einer zum Punkt unendlich. Die Kreise sind nach dem amerikanischen Mathematiker Lester R. Ford benannt, der sie 1938 entdeckte.

Definition

Der Fordkreis zum Bruch $\textstyle\frac{p}{q}$ mit teilerfremden, ganzen Zahlen p,q und $q\geq 0$ wird meist mit C[p / q] oder C[p,q] bezeichnet. Er hat für $q\not=0$ den Radius $\textstyle\frac{1}{2q^2}$ und sein Zentrum liegt im Punkt $\textstyle\left(\frac{p}{q}, \frac{1}{2q^2}\right)$. Außerdem ist der Fordkreis C[1,0] definiert als die Gerade y = 1 (projektiv gesehen ist dies ein Kreis mit Zentrum im Unendlichen).

Eigenschaften der Fordkreise

Das Innere je zweier verschiedener Fordkreise ist disjunkt, d.h. die Kreise überlappen sich nicht. Allerdings können sie sich berühren. Außerdem wird jeder rationale Punkt der x-Achse von einem Fordkreis berührt.

Liegt der Bruch $\textstyle\frac{p}{q}$ im offenen Intervall (0;1), so entsprechen die C[p / q] berührenden Fordkreise gerade den Nachbarn von $\textstyle\frac{p}{q}$ in einer Farey-Reihe.

Siehe auch

• Stern-Brocot-Baum

Literatur

• L. R. Ford, Fractions (American Mathematical Monthly 1938, Ausgabe 45, Nummer 9, Seiten 586--601), auf englisch
• John H. Conway und Richard K. Guy, Zahlenzauber - von natürlichen, imaginären und sonstigen Zahlen, Birkhäuser Verlag 1997 (engl. Original: The Book of Numbers, New York 1996, ISBN 0-387-97993-X)