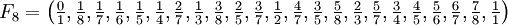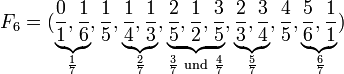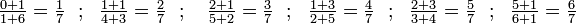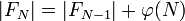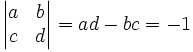Farey-Reihe

Eine Farey-Folge (mathematisch unkorrekt auch Farey-Reihe oder einfach Farey-Brüche) ist in der Zahlentheorie eine geordnete Menge der ausgekürzten Brüche zwischen 0 und 1, deren jeweiliger Nenner den Index N nicht übersteigt. Benannt sind die Farey-Folgen nach dem britischen Geologen John Farey.

Formale Definition

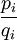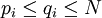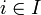Eine Farey-Folge N-ter Ordnung F_N ist eine geordnete Menge von Brüchen $\frac{p_i}{q_i}$ mit $p_i \leq q_i \leq N$, $i \in I$ mit I Indexmenge und 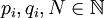$p_i, q_i, N \in \N$, so dass

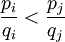$\frac{p_i}{q_i} < \frac{p_j}{q_j}$ für alle 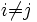$i \not= j$ gilt.

Da in obiger Bedingung Gleichheit untersagt ist, wird stets die gekürzte Form eines Bruches in eine Farey-Folge aufgenommen.

Beispiele

$F_1 = \left( \tfrac{0}{1}, \tfrac{1}{1}\right)$

$F_2 = \left( \tfrac{0}{1}, \tfrac{1}{2}, \tfrac{1}{1}\right)$

$F_3 = \left( \tfrac{0}{1}, \tfrac{1}{3}, \tfrac{1}{2}, \tfrac{2}{3}, \tfrac{1}{1}\right)$

$F_4 = \left( \tfrac{0}{1}, \tfrac{1}{4}, \tfrac{1}{3}, \tfrac{1}{2}, \tfrac{2}{3}, \tfrac{3}{4}, \tfrac{1}{1}\right)$

$F_5 = \left( \tfrac{0}{1}, \tfrac{1}{5}, \tfrac{1}{4}, \tfrac{1}{3}, \tfrac{2}{5}, \tfrac{1}{2}, \tfrac{3}{5}, \tfrac{2}{3}, \tfrac{3}{4}, \tfrac{4}{5}, \tfrac{1}{1}\right)$

$F_6 = \left( \tfrac{0}{1}, \tfrac{1}{6}, \tfrac{1}{5}, \tfrac{1}{4}, \tfrac{1}{3}, \tfrac{2}{5}, \tfrac{1}{2}, \tfrac{3}{5}, \tfrac{2}{3}, \tfrac{3}{4}, \tfrac{4}{5}, \tfrac{5}{6}, \tfrac{1}{1} \right)$.

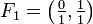
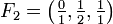
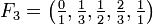
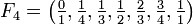
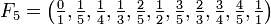
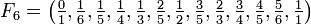Konstruktion

Es gibt wenigstens zwei Wege, eine Farey-Folge zu konstruieren.

Methode 1

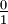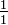Bei der ersten Methode sammelt man zunächst alle notwendigen Brüche und sortiert sie anschließend. Für eine Farey-Folge F_N werden die beiden Brüche $\tfrac{0}{1}$ und $\tfrac{1}{1}$ und alle Brüche gebraucht, deren Nenner q zwischen 2 und N liegen und deren Zähler zwischen 1 und N-1 liegen.

Die Brüche für F₈ sind 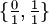$\{\tfrac{0}{1}, \tfrac{1}{1}\}$ und

$q = 2 : \{\tfrac{1}{2}\}$

$q = 3 : \{\tfrac{1}{3}, \tfrac{2}{3}\}$

$q = 4 : \{\tfrac{1}{4}, \tfrac{2}{4}, \tfrac{3}{4}\}$

$q = 5 : \{\tfrac{1}{5}, \tfrac{2}{5}, \tfrac{3}{5}, \tfrac{4}{5}\}$

$q = 6 : \{\tfrac{1}{6}, \tfrac{2}{6}, \tfrac{3}{6}, \tfrac{4}{6}, \tfrac{5}{6}\}$

$q = 7 : \{\tfrac{1}{7}, \tfrac{2}{7}, \tfrac{3}{7}, \tfrac{4}{7}, \tfrac{5}{7}, \tfrac{6}{7}\}$

$q = 8 : \{\tfrac{1}{8}, \tfrac{2}{8}, \tfrac{3}{8}, \tfrac{4}{8}, \tfrac{5}{8}, \tfrac{6}{8}, \tfrac{7}{8}\}$.

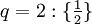
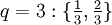
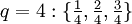
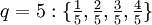
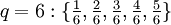
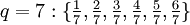
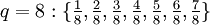Alle möglichen Brüche werden nun soweit wie möglich gekürzt, der Größe nach aufsteigend sortiert, und doppelte Elemente gestrichen:

$F_8 = \left( \tfrac{0}{1}, \tfrac{1}{8}, \tfrac{1}{7}, \tfrac{1}{6}, \tfrac{1}{5}, \tfrac{1}{4}, \tfrac{2}{7}, \tfrac{1}{3}, \tfrac{3}{8}, \tfrac{2}{5}, \tfrac{3}{7}, \tfrac{1}{2}, \tfrac{4}{7}, \tfrac{3}{5}, \tfrac{5}{8}, \tfrac{2}{3}, \tfrac{5}{7}, \tfrac{3}{4}, \tfrac{4}{5}, \tfrac{5}{6}, \tfrac{6}{7}, \tfrac{7}{8}, \tfrac{1}{1} \right)$

Methode 2

Die zweite Methode benutzt eine spezielle Form der Addition von Brüchen. Zur Konstruktion der Folge F_N muss die vorhergehende Farey-Folge F_{N − 1} bekannt sein. Man ergänzt dabei die vorhergehende Farey-Folge um Brüche, die man aus einer Operation jeweils nebeneinander liegender Brüche gewinnt, die aber folgende Bedingung erfüllen müssen: Die Summe der Nenner der beiden Brüche muss N ergeben. 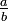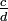Die Operation sieht wie folgt aus: Wenn die beiden, nebeneinander liegenden Brüche $\tfrac{a}{b}$ und $\tfrac{c}{d}$ sind, und die Summe der beiden Nenner b und d = N ist, dann ist der neue Bruch 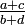$\tfrac{a+c}{b+d}$. Für diese Operation hat sich die Bezeichnung Farey-Addition etabliert. Durch die gemachte Einschränkung 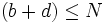$(b+d) \le N$ gilt für jede Farey-Folge, dass sie Teilmenge der Peirce-Zahlen 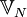$\mathbb V_N \$ ist.

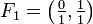Wird $F_1 = \left( \tfrac{0}{1}, \tfrac{1}{1}\right)$ angenommen, ist eine rekursive Konstruktion möglich.

Beispiel

Berechnet werden soll F₇. F₆ wird als bekannt vorausgesetzt, oder selbst erst noch erstellt werden. Mit nebeneinander liegenden Brüchen, deren Nennersumme gleich 7 ist, werden durch Addition von Zähler und Nenner die neuen Elemente gebildet:

$F_6 = ( \underbrace{ \frac{0}{1}, \frac{1}{6}}_{\frac{1}{7}}, \frac{1}{5}, \underbrace{\frac{1}{4}, \frac{1}{3}}_{\frac{2}{7}}, \underbrace{\frac{2}{5}, \frac{1}{2}, \frac{3}{5}}_{\frac{3}{7}\ \mathrm{und}\ \frac{4}{7}}, \underbrace{\frac{2}{3}, \frac{3}{4}}_{\frac{5}{7}}, \frac{4}{5}, \underbrace{\frac{5}{6}, \frac{1}{1}}_{\frac{6}{7}} )$

Die neuen Elemente sind:

$\tfrac{0+1}{1+6} = \tfrac{1}{7} \ \ ; \ \ \tfrac{1+1}{4+3} = \tfrac{2}{7} \ \ ; \ \ \ \tfrac{2+1}{5+2} = \tfrac{3}{7} \ \ ; \ \ \tfrac{1+3}{2+5} = \tfrac{4}{7} \ \ ; \ \ \tfrac{2+3}{3+4} = \tfrac{5}{7} \ \ ; \ \ \tfrac{5+1}{6+1} = \tfrac{6}{7}$

Richtig einsortiert ergibt sich nun

$F_7 = \left( \tfrac{0}{1}, \boldsymbol \tfrac{1}{7}, \tfrac{1}{6}, \tfrac{1}{5}, \tfrac{1}{4}, \boldsymbol \tfrac{2}{7}, \tfrac{1}{3}, \tfrac{2}{5}, \boldsymbol \tfrac{3}{7}, \tfrac{1}{2}, \boldsymbol \tfrac{4}{7}, \tfrac{3}{5}, \tfrac{2}{3}, \boldsymbol \tfrac{5}{7} \ \tfrac{3}{4}, \tfrac{4}{5}, \tfrac{5}{6}, \boldsymbol \tfrac{6}{7}, \tfrac{1}{1} \right)$.

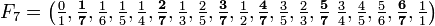Eigenschaften

Die Mächtigkeit einer Farey-Folge ist gleich der Mächtigkeit der Vorgängerfolge addiert mit dem Eulersche φ-Funktion von N:

$|F_N| = |F_{N-1}| + \varphi(N)$

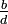Bei zwei aufeinander folgenden Brüchen $\tfrac{a}{c}$ und $\tfrac{b}{d}$ einer Farey-Folge ergeben die Produkte a·d und b·c zwei aufeinander folgende Zahlen. Man kann auch schreiben:

$\begin{vmatrix} a & b \\ c & d \end{vmatrix} = a d - b c = -1$

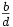Sind umgekehrt $\tfrac ac$ und $\tfrac b d$ zwei Brüche mit 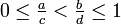$0\le\tfrac{a}{c} < \tfrac {b}{d} \le 1$ und ad − bc = − 1, so handelt es sich um Nachbarn bis zur Farey-Folge F_{c + d − 1}, mit anderen Worten: Jeder dazwischen liegende Bruch 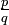$\tfrac {p}{q}$ hat einen Nenner 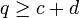$q \ge c+d$. 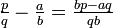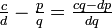In der Tat müssen nämlich die Zähler der positiven Brüche $\tfrac{p}{q} - \tfrac{a}{b} = \tfrac{bp - aq}{qb}$ und $\tfrac{c}{d}-\tfrac{p}{q} = \tfrac{cq - dp}{dq}$ positive ganze Zahlen sein, also 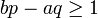$bp - aq \ge 1$ und $cq - dp \ge 1$.

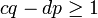Hieraus folgt

$q = (bc-ad) \cdot q = b \cdot (cq-dp) + d \cdot (bp-aq) \ge b+d$.

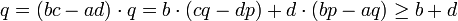Ebenso folgt

$p = (bc-ad) \cdot p = c \cdot (bp-aq) + a \cdot (cq-dp) \ge c+a$.

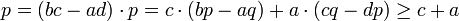Beide Ungleichungen werden scharf genau für die Farey-Summe $\tfrac{p}{q} = \tfrac{a+c}{b+d}$.

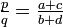Siehe auch

• Ford-Kreise
• Peirce-Zahlen
• Stern-Brocot-Baum

Literatur

• John H. Conway, Richard K. Guy: The Book of Numbers, ISBN 0-387-97993-X
• Scheid, Frommer: Zahlentheorie. 4. Auflage, Spektrum-Verlag.

Weblinks

• Eric W. Weisstein: Farey Sequence auf MathWorld (englisch)
• Farey Series auf cut-the-knot
• Skript zu Fibonacci-Zahlen, Kettenbrüchen und Farey-Folgen
• Horst Hischer 4000 jahre Mittelwertbildung
• Farey Reihen in der Encyclopedia of Mathematics(Springer)