Stern-Brocot-Baum

Die ersten Konstruktionsstufen des Stern-Brocot-Baums

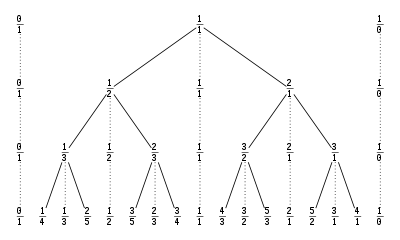
Der Stern-Brocot-Baum ist eine Anordnung aller positiven rationalen Zahlen in Form eines binären Baumes. Er wurde unabhängig voneinander 1858 vom deutschen Mathematiker Moritz Stern und 1860 vom französischen Uhrmacher Achille Brocot entdeckt.

Jeder Knoten des Stern-Brocot-Baums ist als $\tfrac{m+m^\prime}{n+n^\prime}$ definiert, wobei $\tfrac{m}{n}$ der nächste Elternknoten auf der linken und $\tfrac{m^\prime}{n^\prime}$ der nächste auf der rechten Seite ist (einer davon ist der direkte Vorfahre, der andere ein weiter oben stehender). Die Werte ganz links und rechts vom Baum sind hierbei als $\tfrac{0}{1}$ beziehungsweise $\tfrac{1}{0}$ definiert.

Beste Näherungen

Mit Hilfe einer binären Suche auf dem Stern-Brocot-Baum lassen sich beste rationale Näherungen für reelle Zahlen finden. Sie sind beste Näherungen in dem Sinne, dass jede rationale Zahl, die näher am gesuchten Wert liegt, einen größeren Nenner hat.

Die Funktion approximate in folgendem Haskell-Programm generiert die Liste aller besten Näherungen für eine positive reelle Zahl, die als Funktion gegeben ist, welche für jede rationale Zahl angibt, ob sie größer, kleiner, oder gleich der gesuchten ist.

type Ratio = (Integer, Integer)
 
type Interval = (Ratio, Ratio)
 
mediant :: Interval -> Ratio
mediant ((m, n), (m', n')) = (m+m', n+n')
 
approximate :: (Ratio -> Ordering) -> [Ratio]
approximate c = h ((0,1),(1,0)) where
    h interval@(lo, hi) = mid : case c mid of
        LT -> h (mid, hi)
        GT -> h (lo, mid)
        EQ -> []
        where mid = mediant interval

Die generierte Liste ist endlich, wenn die gesuchte Zahl rational ist.