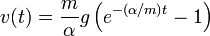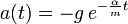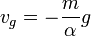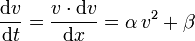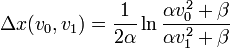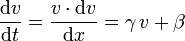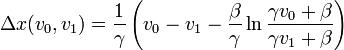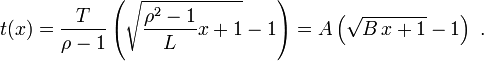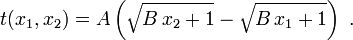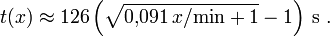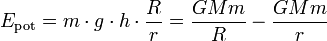- Formelsammlung Mechanik
-
Inhaltsverzeichnis
Kinematik
Geradlinige Bewegung
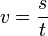
- v = Geschwindigkeit in m/s
- s = Strecke in m
- t = Zeit in s
Gleichförmige Kreisbewegung
- (v = konstant)
- b = Bogenlänge in m
- r = Radius in m
 = Winkelkoordinate rad (Radiant = keine deklarierte Einheit)
= Winkelkoordinate rad (Radiant = keine deklarierte Einheit)- ω = Winkelgeschwindigkeit in rad/s = 1/s
- f = Frequenz in 1/s = Hz
- v = Bahngeschwindigkeit in m/s
- T = Umlaufzeit in s
- az = Zentripetalbeschleunigung in m/s^2
Geradlinige gleichförmige Bewegung
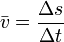
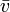 = mittlere Geschwindigkeit in m / s
= mittlere Geschwindigkeit in m / s- Δs = Strecke in m
- Δt = Zeit in s
Mittlere Geschwindigkeiten Typ m / s Schnecke 0,002 Fußgänger 1,4 Regentropfen 6 Brieftaube 20 Rennpferd bis 25 Erde bei 0° Breite 464 Gewehrkugel 870 Licht 299.792.458 Gleichmäßig beschleunigte Bewegung
mit
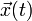 = zeitabhängige Position
= zeitabhängige Position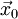 = Anfangsposition
= Anfangsposition = zeitabhängige Geschwindigkeit
= zeitabhängige Geschwindigkeit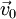 = Anfangsgeschwindigkeit
= Anfangsgeschwindigkeit = Beschleunigung
= Beschleunigung- t = Zeit
Der Spezialfall
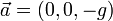 entspricht dem schrägen Wurf ohne Luftwiderstand. Die Bewegungskomponente in waagerechter Richtung ist dann gleichförmig, während die vertikale Bewegungskomponente eine gleichförmig beschleunigte ist.
entspricht dem schrägen Wurf ohne Luftwiderstand. Die Bewegungskomponente in waagerechter Richtung ist dann gleichförmig, während die vertikale Bewegungskomponente eine gleichförmig beschleunigte ist.Im weiteren Spezialfall einer gleichförmigen Beschleunigung entlang einer Linie vereinfacht sich der Ausdruck als
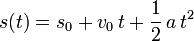
- s = Strecke
Mittlere Beschleunigung Typ m / s² Personenzug 0,15 U-Bahn 0,60 Personenaufzug 2 Rakete 30 Freier Fall ohne Reibung
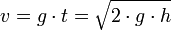
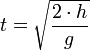
- v = Geschwindigkeit in m / s
- g = Erdbeschleunigung in m / s²
- t = Zeit in s
- h = Fallhöhe in m
Erdbeschleunigung Ort m / s² Äquator 9,78 Nord- und Südpol 9,83 Normwert 9,80665 Freier Fall mit Reibung
Gegeben: Anfangshöhe H, Schwerebeschleunigung g.
Gesucht: Zeitliche Entwicklung von Momentanhöhe h(t), Geschwindigkeit v(t) und Beschleunigung a(t), Grenzgeschwindigkeit v(∞) (negatives Vorzeichen: abwärts gerichtet)
Fall 1: Newton-Reibung
![h(t) = H-\frac{m}{\alpha}\ln\left[\cosh\left(\sqrt{\frac{\alpha g}{m}}\cdot t\right)\right]](/pictures/dewiki/97/af7f9642ab4f16ed31ed0258acf341c9.png)
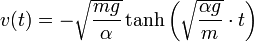
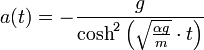
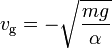 = Grenzgeschwindigkeit
= Grenzgeschwindigkeit
Im Newton-Fall ist
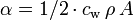 , mit
, mit- cw = Strömungswiderstandskoeffizient
- ρ = Luftdichte
- A = Stirnfläche des fallenden Körpers
Beispiel: Fallschirmspringer mit
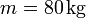 ,
,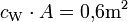 springt aus H = 4000 m aus einem Ballon (Anfangsgeschwindigkeit = 0 m/s). Mittlere Luftdichte = ca. 1 kg/m3, ergo α = 0,3kg / m. Ferner g = 9,8 m/s2.
springt aus H = 4000 m aus einem Ballon (Anfangsgeschwindigkeit = 0 m/s). Mittlere Luftdichte = ca. 1 kg/m3, ergo α = 0,3kg / m. Ferner g = 9,8 m/s2.
Nach t = 10 s:
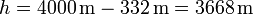 ,
,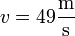 = 96% der Grenzgeschwindigkeit (51 m/s),
= 96% der Grenzgeschwindigkeit (51 m/s),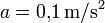 = 1% von g.
= 1% von g.
Nach t = 1 min ist:
Zur Genauigkeit: Für obiges Beispiel sind die Fehler im Vergleich zum numerisch Integrierten Modell nach Standardatmosphäre, konstantem cw und ρ = ρ(H/2) in h kleiner als 100 m (bzw. 2 s), in v kleiner als 5 m/s und in a kleiner als 0,6 m/s² = 0,06 g. Für größere H nehmen die Fehler wegen ρ(H) stark zu. Schwer quantifizierbare Fehler sind in wegen veränderlicher Körperhaltung (Fallschirmspringer) oder strömungsphysikalisch bedingter Veränderlichkeit von cw (auch z.B. bei starren Kugeln) zu erwarten.Fall 2: Stokes-Reibung
Bremsweg mit zwei Reibungskomponenten
Newton- und trockene Reibung
Gegeben sei eine Reibungsverzögerung der Form
Dabei α wie im Newton-gebremsten Fall definiert und β die konstante (trockene) Reibung. Dann ist der Bremsweg Δx von v0 auf v1 mit v0 ≥ v1 ≥ 0
Stokes- und trockene Reibung
Gegeben sei eine Reibungsverzögerung der Form
Dann ist der Bremsweg Δx von v0 auf v1 mit v0 ≥ v1 > 0
Spulzeit von Tonbändern
Problem: Auffinden einer Bandstelle (in Spielminuten) bei einem Tonband- oder Videorecorder ohne oder nur mit einfachem Zählwerk (Umdrehungszähler).
Bekannte Größen: Bandlänge L in Spielminuten, Umspulzeit bzw. Zählerdifferenz nach vollständigem Umspulen T, Verhältnis des Radius der vollen zur leeren Spule ρ = Rvoll / Rleer.
Für eine beliebige Bandstelle x in Spielminuten ist die Spulzeit (vom Bandanfang) bzw. der Zählerstand dann
Analog ist die Spulzeit oder Zählwerksdifferenz von der Position x1 zu x2 gespult werden, so gilt
Für eine typische 90-min-Audiocassette ist L = 46 min, ρ = 25/11 und T = 160 s und somit
Dynamik
Kraft
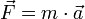
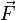 = Kraft in N
= Kraft in N- m = Masse in kg
 = Beschleunigung in m / s²
= Beschleunigung in m / s²
Gewichtskraft
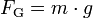
- FG = Gewichtskraft in N
- m = Masse in kg
- g = Fallbeschleunigung in m / s²
Gravitationskraft
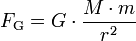
- FG = Gravitationskraftkraft in N
- m1 = Masse des einen Körpers in kg
- m2 = Masse des anderen Körpers in kg
- r = Entfernung der Schwerpunkte beider Körper voneinander in m
- G = Gravitationskonstante
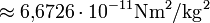
Reibung
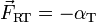 = trockene Reibung (Gleitreibung)
= trockene Reibung (Gleitreibung)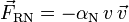 Newtonsche Reibung
Newtonsche Reibung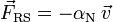 Stokessche Reibung
Stokessche Reibung
Hebelgesetz
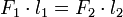
- F1 = Kraft in N
- F2 = Last in N
- l1 = Kraftarmlänge in m
- l2 = Lastarmlänge in m
Drehmoment
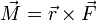
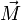 = Drehmoment in Nm
= Drehmoment in Nm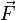 = Kraft in N
= Kraft in N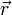 = Hebelarmlänge in m
= Hebelarmlänge in m
Arbeit
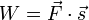
- W = Arbeit in Nm (1 Nm = 1 J = 1 Ws)
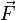 = Kraft in N
= Kraft in N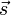 = Weg in m
= Weg in m
Potentielle Energie
Hubarbeit (Gilt nur nahe der Oberfläche eines Himmelskörpers)
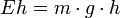
- W = Arbeit in Nm (1 Nm = 1 J = 1 Ws)
- m = Masse des Körpers in kg
- g = Fallbeschleunigung in m / s²
- h = Hubhöhe in m
Potentielle Energie in einem Gravitationsfeld
- Epot = Potentielle Energie in J
- M = Masse des Himmelskörpers in kg
- R = Radius des Himmelskörpers in m
- r = Radius des Himmelskörpers + Hubhöhe (R+h) in m
- G = Gravitationskonstante
Siehe hierzu auch: Potentielle Energie.
Maximale potentielle Energie in einem Gravitationsfeld
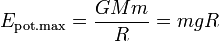 , mit GM = gR2
, mit GM = gR2
Potentielle Energie einer gespannten Feder
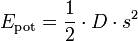
- D = Federkonstante
- s = Auslenkung der Feder aus der Ruhelage
Kinetische Energie
Beschleunigungsarbeit
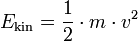
- Ekin = Arbeit in Nm (1 Nm = 1 J = 1 Ws)
- m = Masse in kg
- v = Geschwindigkeit in m / s
Leistung
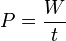
- P = Leistung in Nm / s (1 Nm / s = 1 J / s = 1 W)
- W = Arbeit in Nm (1 Nm = 1 J = 1 Ws)
- t = Zeit in s
Wikimedia Foundation.

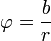
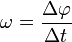
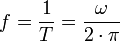
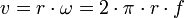
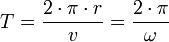
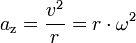
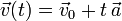
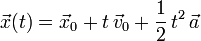
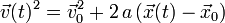
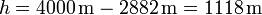
![h(t)=H+\frac{m}{\alpha}g\left[\frac{m}{\alpha}\left(1-e^{-(\alpha/m)t}\right)-t\right]](/pictures/dewiki/56/857a0eafc2e5afc07715a16f947a0739.png)