Geburtstagsangriff

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Die Artikel Geburtstagsangriff und Kollisionsangriff überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Fjellheisen 07:46, 17. Jul. 2007 (CEST)

Ein Geburtstagsangriff ist eine Methode, für eine gegebene Hash-Funktion verschiedene Dokumente mit gleichem Hash-Wert zu finden. Der Name wurde gewählt, da es sich um eine Anwendung des mathematischen Modells handelt, welches auch das Geburtstagsparadoxon zu beschreiben vermag.

Der naive Brute-Force-Angriff auf eine Hash-Funktion besteht darin, zu einem gegebenen Text einen anderen Text zu finden, der den gleichen Hash-Wert hat. Bei einem Hash-Wert von 40 Bit sind dafür etwa eine Billion Versuche nötig.

In vielen Missbrauchsszenarien können aber beide Texte variiert werden. Dabei handelt es sich dann um einen Geburtstagsangriff, und die nötige Zahl an Variationen ist nur noch etwas größer als die Quadratwurzel der benötigten Anzahl beim naiven Angriff, also für einen 40-Bit-Hash etwas über eine Million Versuche.

Vorgehensweise

Erstelle Variationen von „guten“ Texten zum Beispiel durch Festlegen von veränderlichen Inhalten, die dem Betrachter nicht auffallen. Werden beispielsweise 32 Positionen festlegt, die jeweils auf zwei Arten ausgeführt werden können, so ergeben sich 2³² (etwa 4.000.000.000) verschiedene Dokumente.

Danach wird eine große Variation von „bösen“ Texten erstellt. Der Angreifer vergleicht nun beide Mengen und hofft, auf je ein Dokument mit dem gleichen Hash-Wert zu treffen. Dieses weicht etwas vom eigentlichen Geburtstagsparadoxon ab, da es erforderlich ist, ein Paar zu finden, bei dem einer der Texte zu den „guten“ und einer zu den „bösen“ gehört und es nicht reicht, zum Beispiel zwei „gute“ Texte mit demselben Hash-Wert zu finden.

Um dem Erfolg eines Geburtstagsangriffs entgegenzuwirken, muss die Länge des Hashwertes hinreichend groß gewählt werden, so dass Überschneidungen auch mit diesem Verfahren sehr unwahrscheinlich werden. Für elektronische Unterschriften etwa sind derzeit 160 Bit gebräuchlich. Eine weitere Möglichkeit, dem Geburtstagsangriff entgegenzuwirken, ist die Veränderung des Dokumentes kurz vor der Unterschrift. Damit kann die „Vorbereitung“ der Texte ausgeschlossen werden.

Beispiel für die Anwendung

Elektronische Unterschriften beziehen sich auf den Hash-Wert der unterzeichneten Dokumente, nicht auf den tatsächlichen Inhalt. Der Angreifer erzeugt also zunächst zwei verschiedene Verträge: Einen „guten“ Vertrag mit günstigen Konditionen für das Opfer und einen „schlechten“ Vertrag mit günstigen Konditionen für den Angreifer. Durch geringfügige Veränderungen (etwa das Einfügen von Leerzeichen) werden dabei beide Verträge so lange variiert, bis sie den gleichen Hash-Wert haben, ohne dass sich ihr jeweiliger Inhalt ändert.

Dann wird dem Opfer der „gute“ Vertrag zur elektronischen Unterschrift vorgelegt. Die erstellte Signatur bezieht sich auf den gemeinsamen Hash-Wert der beiden Verträge, kann also auch missbräuchlich für den „schlechten“ Vertrag verwendet werden.

Der Unterzeichner kann dieser Attacke entgegenwirken, indem er vor dem Unterschreiben ebenfalls irrelevante Änderungen durchführt, also beispielsweise ein zusätzliches Leerzeichen einfügt. Diese Gegenmaßnahme funktioniert natürlich nur, wenn der Vertrag nicht bereits unterzeichnet ist und nur noch gegengezeichnet werden muss.

Anderenfalls wäre es besser, den Hash-Algorithmus mit einem Zufallswert (seed) zu starten und als Unterschrift sowohl seed als auch Hash-Wert zu verwenden. Übliche digitale Signaturverfahren unterstützen diese Modifikation nicht.

Bei gebräuchlichen Hash-Funktionen wie SHA-1 ist jedoch die Wahrscheinlichkeit für eine zufällig auftretende Übereinstimmung bzw. Kollision der Hash-Werte (p = 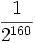${1}\over{2^{160}}$) der beiden Vertragsversionen praktisch zu vernachlässigen. Eine solche Kollision kann im Grunde nur auftreten, wenn eine absichtliche Manipulation vorliegt, wie oben beschrieben. Der Angreifer kann das gefälschte Dokument damit praktisch nicht als Beweis vorlegen, da die Kollision des Hash-Wertes mit dem Hash-Wert der tatsächlich vom Unterzeichner signierten Version die absichtliche Manipulation aufdeckt.