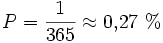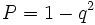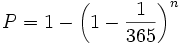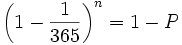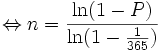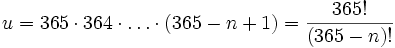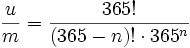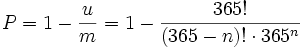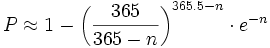Fussballerwette

Das Geburtstagsparadoxon, manchmal auch als Geburtstagsproblem bezeichnet, ist ein Beispiel dafür, dass bestimmte Wahrscheinlichkeiten (und auch Zufälle) intuitiv häufig falsch abgeschätzt werden.

Das Ergebnis der Frage

Wie hoch ist die Wahrscheinlichkeit, dass bei 23 Personen auf einem Fußballfeld (22 Spieler und ein Schiedsrichter) zwei von ihnen am selben Tag Geburtstag haben (ohne Beachtung des Jahrganges)?

ist für die meisten verblüffend und wird deshalb als paradox wahrgenommen. So schätzen die meisten Menschen die Wahrscheinlichkeit um eine Zehnerpotenz falsch ein. Sie liegt nicht zwischen 1 und 5 % (wie zumeist geschätzt), sondern über 50 %; bei 50 Personen sogar bei über 97 %.

Im Unterschied dazu steht die Wahrscheinlichkeit, dass jemand an einem ganz bestimmten Tag Geburtstag hat: wenn man sich zum Beispiel den Schiedsrichter nimmt und fordert, dass jemand mit genau ihm am selben Tag Geburtstag hat. Für diesen Fall sind 253 Personen notwendig, um eine Wahrscheinlichkeit von 50 % zu erreichen (siehe Binomialverteilung).

Der Grund für diesen großen Unterschied liegt darin, dass es bei n Personen n(n − 1) / 2 verschiedene Paare gibt, die am selben Tag Geburtstag haben könnten. Die Wahrscheinlichkeit für das Zusammentreffen beziehungsweise Kollidieren zweier Geburtstage steigt daher ungefähr mit dem Quadrat der Anzahl n an.

Dieser Effekt hat eine Bedeutung bei kryptographischen Hash-Funktionen, die einen eindeutigen Prüfwert aus einem Text ergeben sollen. Es ist dabei viel einfacher, zwei zufällige Texte zu finden, die denselben Prüfwert haben, als zu einem vorgegebenen Text einen weiteren zu finden, der denselben Prüfwert aufweist (siehe Geburtstagsangriff).

Mathematische Herleitungen

Im Folgenden wird der 29. Februar vernachlässigt und angenommen, dass die Geburtstage der n Personen unabhängig identisch verteilte Zufallsvariablen aus der diskreten Gleichverteilung auf der 365-elementigen Menge 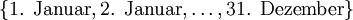$\{\mbox{1. Januar}, \mbox{2. Januar}, \dots, \mbox{31. Dezember}\}$ sind. Diese Annahme ist beispielsweise dann nicht erfüllt, wenn sich unter den n anwesenden Personen Zwillinge befinden.

Im Urnenmodell entspricht diese Annahme einer Ziehung von n Kugeln mit Zurücklegen aus einer Urne, die 365 Kugeln mit der Beschriftung „1. Januar“, „2. Januar“, bis "31. Dezember" enthält.

Wahrscheinlichkeit für einen bestimmten Tag

Unter der getroffenen Annahme ist die Wahrscheinlichkeit, an einem bestimmten Tag Geburtstag zu haben:

$P = {1\over365}\approx0{,}27\ \%$

Da die Wahrscheinlichkeit für das Gegenteil (es gibt keine zwei Leute, die am selben Tag Geburtstag haben) unter einem bestimmten Schwellwert (in diesem Fall 50 %) liegen soll, muss über das Gegenereignis gerechnet werden. Die Wahrscheinlichkeit, an einem bestimmten Tag nicht Geburtstag zu haben, ist

$q = 1-{1\over365}\approx99{,}73\ \%$.

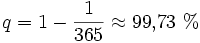Bei zwei unabhängigen Versuchen (die Geburtstage zweier Personen werden als unabhängig betrachtet) ist die Wahrscheinlichkeit, keinen Treffer zu haben (am bestimmten Tag hat keiner von beiden Geburtstag): Q = q²

Dabei mindestens einen Treffer zu haben (mindestens eine Person von zweien hat an einem bestimmten Tag Geburtstag), ist wieder die Gegenwahrscheinlichkeit, also:

$P = 1-q^2\,$

Allgemein ausgedrückt ist die Wahrscheinlichkeit P, mit der mindestens eine Person von n anwesenden Personen an einem bestimmten Tag Geburtstag hat:

$P = 1-\left(1-{1\over365}\right)^n$

Damit lässt sich ausrechnen, wie viele Personen n man braucht, um eine bestimmte Wahrscheinlichkeit zu erreichen, dass mindestens eine Person an einem bestimmten Tag Geburtstag hat:

$\left(1-{1\over365}\right)^n = 1-P$

$\Leftrightarrow n = {{\ln(1-P)}\over{\ln(1-{1\over365})}}$

Für eine Wahrscheinlichkeit von 50 % benötigt man:

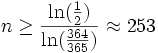$n \ge {{\ln({1\over2})}\over{\ln({364\over365})}} \approx 253$ Teilnehmer

Wahrscheinlichkeit, dass mindestens zwei Personen an einem Tag Geburtstag haben

Die Anzahl aller möglichen Fälle ist für n Personen m = 365ⁿ, wobei alle Fälle gleich wahrscheinlich sind. Zum Beispiel ergeben sich für zwei Personen 365² = 133225 mögliche Fälle von Geburtstagskombinationen.

Von diesen möglichen Fällen beinhalten

$u = 365 \cdot 364 \cdot \dots \cdot (365-n+1) = \frac{365!}{(365-n)!}$

nur unterschiedliche Geburtstage. Für die erste Person kann der Geburtstag frei gewählt werden, für die zweite gibt es dann 364 Tage, an denen die erste nicht Geburtstag hat etc.

p(n) = Wahrscheinlichkeit für mindestens einen doppelten Geburtstag
q(n) = Wahrscheinlichkeit, dass ein Geburtstag mit deinem zusammenfällt

Damit ergibt sich nach der Formel von Laplace die Wahrscheinlichkeit von

$\frac{u}{m} = \frac{365!}{(365-n)!\cdot365^n}$

dass alle n Personen an unterschiedlichen Tagen Geburtstag haben.

Die Wahrscheinlichkeit für mindestens einen doppelten Geburtstag ist somit

$P=1-\frac{u}{m}=1-\frac{365!}{(365-n)!\cdot365^n}$

Mit der Stirling-Formel lässt sich dies gut nähern zu

$P \approx 1 - \left(\frac{365}{365-n}\right)^{365.5 - n}\cdot e^{-n}$

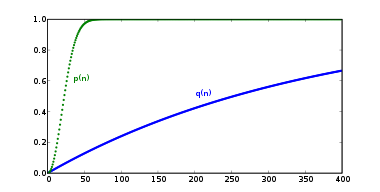
Berechnet man etwa für n=10, 11, …, bis 23 mit einem Taschenrechner P nach der oben angegebenen Formel, kommt man zu dem Ergebnis, dass für eine Wahrscheinlichkeit von mindestens 50 % nur 23 Personen benötigt werden. In Gruppen größer als 57 Personen beträgt die Wahrscheinlichkeit schon über 99 %.

Siehe auch: Lincoln-Kennedy-Mysterium

Ungleichmäßig verteilte Geburtstage

In der Realität sind nicht alle Geburtstermine gleich wahrscheinlich, so werden z. B. im Sommer mehr Kinder geboren als im Winter ^[1]. Es lässt sich aber zeigen, dass für nicht gleichmäßig verteilte Geburtstage die Wahrscheinlichkeit zunimmt, dass zwei Personen am selben Tag Geburtstag haben^[2][3]. In der Realität spielt die Abweichung von der Gleichverteilung keine besondere Rolle; Simulationen zeigen, dass auch für echte Daten die Wahrscheinlichkeiten, dass zwei Personen am gleichen Tag Geburtstag haben, nach wie vor bei 23 Personen 50 % übersteigt ^[4].

Ebenso ist die Vernachlässigung des Schalttages in der Herleitung kein Problem; würde man statt mit 365 mit 366 Tagen rechnen, erhält man dasselbe Ergebnis (ab 23 Personen eine Wahrscheinlichkeit größer als 0,5).

Geschichte

Das Geburtstagsparadoxon wird oft Richard von Mises zugeschrieben^[5]. Laut Donald Ervin Knuth ist dieser Ursprung nicht so sicher: Das Geburtstagsparadoxon wurde informell unter Mathematikern in den 1930er Jahren diskutiert, ein genauer Urheber lässt sich aber nicht nachvollziehen.^[6]

Quellen

1. ↑ Emma Hawe, Alison Macfarlane and John Bithell: Daily and seasonal variation in live births, stillbirths and infant mortality in England and Wales, 1979–96 in Health Statistics Quarterly 9 Spring 2001 S 7: There was a clear seasonal pattern in the number of daily live births throughout the entire period, with lower numbers of births in the winter than the summer months.
2. ↑ Bloom, D. (1973), A birthday problem, American Mathematical Monthly, vol. 80, S. 1141–1142 enthält einen Beweis mit Lagrange-Multiplikatoren, dass für nicht gleichmäßig verteilte Geburtstage die Wahrscheinlichkeit zunimmt, dass zwei Personen am selben Tag Geburtstag haben.
3. ↑ Stefan Kirchner in de.sci.mathematik, 3. Nov. 2005
4. ↑ Hugo Pfoertner in de.sci.mathematik, 22. Jan. 2005
5. ↑ z.B. http://www25.brinkster.com/ranmath/problems/birthday.htm
6. ↑ Donald E. Knuth: The Art of Computer Programming, Volume 3, Sorting and Searching. Second Edition, ISBN 0201896850. S. 513.

Weblinks

• http://www.im-chaos-daheim.de/geburtstag.php: Ein Applet zum Berechnen der Wahrscheinlichkeiten