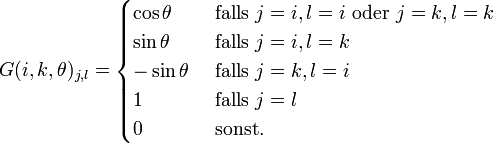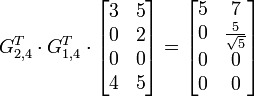Givensrotation

In der linearen Algebra ist eine Givens-Rotation (nach Wallace Givens) eine Drehung in einer Ebene, die durch zwei Koordinaten-Achsen aufgespannt wird. Manchmal wird dies auch als Jacobi-Rotation (nach Carl Gustav Jacobi) bezeichnet.

Beschreibung

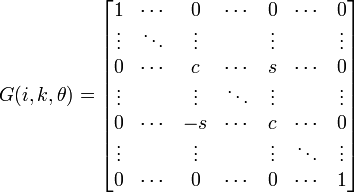
Die Transformation lässt sich durch eine Matrix der Form

$G(i, k, \theta) = \begin{bmatrix} 1 & \cdots & 0 & \cdots & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & & \vdots & & \vdots \\ 0 & \cdots & c & \cdots & s & \cdots & 0 \\ \vdots & & \vdots & \ddots & \vdots & & \vdots \\ 0 & \cdots & -s & \cdots & c & \cdots & 0 \\ \vdots & & \vdots & & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & \cdots & 0 & \cdots & 1 \end{bmatrix}$

beschreiben, wobei c = cos(θ) und s = sin(θ) in der i-ten und k-ten Zeile und Spalte erscheinen. Eine solche Matrix heißt Givens-Matrix. Formaler ausgedrückt:

$G(i, k, \theta)_{j, l} = \begin{cases} \cos\theta & \mbox{ falls } j = i, l = i \mbox{ oder } j = k, l = k \\ \sin\theta & \mbox{ falls } j = i, l = k \\ -\sin\theta & \mbox{ falls } j = k, l = i \\ 1 & \mbox{ falls } j = l \\ 0 & \mbox{ sonst. } \end{cases}$

Das Produkt G^T(i,k,θ)x stellt eine Drehung des Vektors x um einen Winkel θ in der (i,k)-Ebene dar, diese wird Givens-Rotation genannt.

Die Hauptanwendung der Givens-Rotation liegt in der numerischen linearen Algebra, um Nulleinträge in Vektoren und Matrizen zu erzeugen. Dieser Effekt kann beispielsweise bei der Berechnung der QR-Zerlegung einer Matrix ausgenutzt werden. Außerdem werden solche Drehmatrizen beim Jacobi-Verfahren benutzt.

QR-Zerlegung mittels Givens-Rotationen

• Das Verfahren ist sehr stabil. Pivotisierung ist nicht erforderlich.
• Flexible Berücksichtigung von schon vorhandenen 0-Einträgen in strukturierten (insbesondere dünnbesetzten) Matrizen.
• Die Idee besteht darin, sukzessiv die Elemente unterhalb der Hauptdiagonalen auf Null zu setzen, indem man die Matrix von links mit Givens-Rotationen multipliziert. Zunächst bearbeitet man die erste Spalte von oben nach unten und dann nacheinander die anderen Spalten ebenfalls von oben nach unten.
• Man muss also 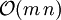$\mathcal{O}(m\,n)$ Matrixmultiplikationen durchführen. Da sich jeweils pro Multiplikation höchstens 2n Werte verändern, beträgt der Aufwand für eine QR-Zerlegung einer vollbesetzten m x n-Matrix insgesamt 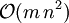$\mathcal{O}(m\,n^2)$. Für dünn besetzte Matrizen ist der Aufwand allerdings erheblich niedriger.
• Will man a_ij = 0 erreichen, so setzt man c = a_jj / ρ und s = a_ij / ρ, wobei $\rho = \sgn(a_{jj}) \sqrt{a_{jj}^2 + a_{ij}^2}$.

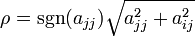Beispiel (QR-Zerlegung):

$G_{2,4}^T\cdot G_{1,4}^T\cdot \begin{bmatrix} 3 & 5\\ 0 & 2\\ 0 & 0\\ 4 & 5 \end{bmatrix} = \begin{bmatrix} 5 & 7\\ 0 & \frac{5}{\sqrt{5}}\\ 0 & 0\\ 0 & 0 \end{bmatrix}$

mit

$G_{1,4}^T = \begin{bmatrix} \frac{3}{5} & 0 & 0 & \frac{4}{5} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \frac{-4}{5} & 0 & 0 & \frac{3}{5} \end{bmatrix}$, $G_{2,4}^T = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \frac{2}{\sqrt{5}} & 0 & -\frac{1}{\sqrt{5}} \\ 0 & 0 & 1 & 0 \\ 0 & \frac{1}{\sqrt{5}} & 0 & \frac{2}{\sqrt{5}} \\ \end{bmatrix}$

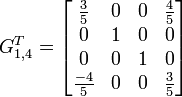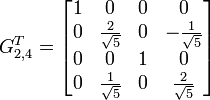
Literatur

• Gene H. Golub, Charles F. van Loan: Matrix Computations. 2nd Edition. The Johns Hopkins University Press, 1989.