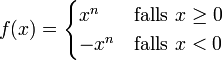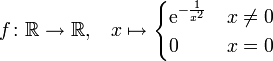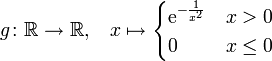Glattheit

Eine mathematische Funktion ist eine glatte Funktion, wenn sie beliebig oft differenzierbar ist. Ebenso gebräuchlich dafür ist der Begriff unendlich oft differenzierbar.

Dabei ist die Bezeichnung glatt durch die Anschaulichkeit motiviert: Der Graph einer unendlich oft differenzierbaren Funktion und somit auch die Graphen aller Ableitungen haben keine „Ecken“, also Stellen, an denen sie nicht differenzierbar sind. Damit wirkt der Graph überall „besonders glatt“.

Definition

Der reelle Fall

Für eine nichtleere, offene Teilmenge 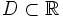$D \subset \mathbb R$ bezeichnet man die Menge der reellwertigen und auf ganz D stetigen Funktionen mit C(D), C⁰(D) oder auch 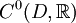$C^0(D,\mathbb R)$. Entsprechend wird die Menge der einmal bzw. für eine natürliche Zahl n die Menge der n-mal stetig differenzierbaren Funktionen mit C¹(D) bzw. Cⁿ(D) bezeichnet. Rekursiv formuliert:

$f \in C^n(D) \Leftrightarrow f\in C^1(D) \text{ und } f' \in C^{n-1}(D)$.

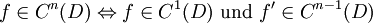Es gilt stets

$C^n(D)\subset C^{n-1}(D) \subset \cdots \subset C^1(D) \subset C^0(D)$.

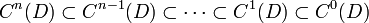Damit kann man nun folgende Definition formulieren:

Definition

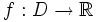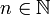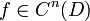Eine Funktion $f: D \to \mathbb R$ heißt unendlich oft differenzierbar, wenn sie beliebig oft differenzierbar ist, wenn also für alle $n \in \mathbb N$ gilt: $f \in C^n(D)$. Die Menge aller unendlich oft differenzierbaren Funktionen auf D wird mit 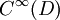$C^\infty(D)$ bezeichnet. Es gilt also:

$C^\infty(D) := \bigcap_{n \in \mathbb N} C^n(D)$.

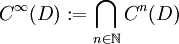Diese Beschreibung ist insbesondere für topologische Betrachtungen nützlich.

Verallgemeinerungen

Ohne Schwierigkeiten lässt sich der Begriff unendlich oft differenzierbar auf alle Fälle verallgemeineren, in denen Differenzierbarkeit definiert werden kann. Die Funktion kann ein Skalarfeld oder ein Vektorfeld sein: 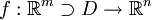$f: \mathbb R^m \supset D \to \mathbb R^n$ ist unendlich oft differenzierbar und damit glatt, wenn alle partiellen Ableitungen beliebig oft differenzierbar sind.

Ebenso werden auch glatte Funktionen zwischen differenzierbaren Mannigfaltigkeiten betrachtet.

Eigenschaften

• Notwendigerweise sind sämtliche Ableitungen stetig, da sonst die jeweils nächste Ableitung nicht gebildet werden könnte.

• Häufig findet man in mathematischen Betrachtungen den Begriff hinreichend glatt. Hiermit ist gemeint, dass die Funktion für ein hinreichend großes n in Cⁿ(D) liegt, also gerade so oft differenzierbar ist, um den aktuellen Gedankengang durchzuführen. Dies wird so formuliert, um eine zu starke (und nicht sinnvolle) Einschränkung durch „unendlich oft differenzierbar“ zu vermeiden. Theoretisch ergeben sich kaum Unterschiede, da für alle 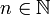$n \in \mathbb N$ die n-fach differenzierbaren und auch die unendlich oft differenzierbaren Funktionen dicht in den stetigen liegen. Ist aus dem Kontext erkennbar, dass nur hinreichend glatte Funktionen betrachtet werden (z.B. durch Angabe des Grades der Differenzierbarkeit) wird auf den Zusatz "hinreichend" gelegentlich auch verzichtet.

• Zusätzlich bezeichnet man noch mit C^ω(D) die Menge aller analytischen Funktionen, das sind die glatten Funktionen, deren Taylor-Entwicklung um jeden beliebigen Punkt in einer Umgebung gegen die gegebene Funktion konvergiert. Beachtenswert ist dann, dass jede der folgenden Inklusionen 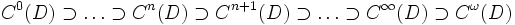$C^0(D) \supset \ldots \supset C^n(D)\supset C^{n+1}(D)\supset \ldots \supset C^\infty(D)\supset C^\omega(D)$ im reellwertigen Fall echt ist. Im Falle komplexwertiger und komplex differenzierbarer, besser gesagt holomorpher Funktionen, ist jede auf einer offenen Menge komplex differenzierbare Funktion gleich unendlich oft differenzierbar und sogar analytisch. Deswegen bezieht sich die Differenzierbarkeit bei Cⁿ(D) meist auf reellwertige Funktionen.

• Jeder Cⁿ(D) und auch 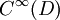$C^\infty(D)$ (sowie C^ω(D)) ist ein (unendlichdimensionaler) Vektorraum.

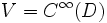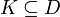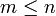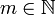• Metrisierung: Sei V = Cⁿ(D) bzw. $V=C^\infty(D)$. Ist $K\subseteq D$ kompakt und $m\leq n$ (bzw. $m\in \mathbb{N}$ beliebig im Fall 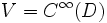$V=C^\infty(D)$), so definiert 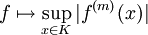$f\mapsto \sup_{x\in K} |f^{(m)}(x)|$ eine Halbnorm auf V. Hat man eine aufsteigende Folge von Kompakta, die D ausschöpfen, so definiert die entsprechende abzählbare Folge von Halbnormen auf V eine Fréchet-Metrik und macht V zu einem Fréchet-Raum.

Beispiele

• Alle Polynomfunktionen sind glatt und sogar analytisch.
• Die durch

$f(x) = \begin{cases} x^n & \text{falls } x \ge 0\\ -x^n & \text{falls } x < 0 \end{cases}$

definierte Funktion ist (n − 1)-mal stetig differenzierbar (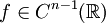$f \in C^{n-1}(\R)$), die (n − 1)-te Ableitung 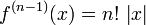$f^{(n-1)}(x) = n! \, \left| x \right|$ ist jedoch an der Stelle x = 0 nicht stetig differenzierbar, also $f \notin C^n(\R)$.

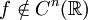• Die Funktion

$f\colon\mathbb R \to \mathbb R,\;\;\; x\mapsto \begin{cases} \mathrm e^{-\frac{1}{x^2}} & x\neq 0 \\ 0 & x=0 \end{cases}$

ist eine glatte Funktion, aber keine analytische Funktion, denn die Taylorreihe um den Nullpunkt stimmt in keiner Umgebung um 0 mit der Funktion überein, da alle Ableitungen bei 0 den Wert 0 annehmen.

• Ebenso ist aber auch

$g\colon\mathbb R \to \mathbb R,\;\;\; x\mapsto \begin{cases} \mathrm e^{-\frac{1}{x^2}} & x> 0 \\ 0 & x\leq 0 \end{cases}$

glatt. Aus lokaler Kenntnis einer glatten Funktion kann man also offensichtlich keine globalen Aussagen herleiten (hier gilt etwa f(x) = g(x) für alle positiven x, aber dennoch $f\neq g$).

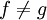Anwendung

Diese beiden letzten Beispiele sind wichtige Hilfsmittel zur Konstruktion von Beispielen von glatten Funktionen mit besonderen Eigenschaften. Auf folgende Weise kann man eine glatte Zerlegung der Eins (hier: von $\mathbb R$) konstruieren:

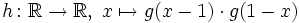• $h\colon\mathbb R \to \mathbb R,\; x\mapsto g(x-1)\cdot g(1-x)$ ist glatt mit kompaktem Träger [ − 1,1].

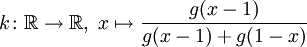• $k\colon\mathbb R \to \mathbb R,\; x\mapsto \frac{g(x-1)}{g(x-1) + g(1-x)}$ ist glatt und es gilt

$k(x)=0 \quad \mathrm{f\ddot ur} \quad x\leq -1$,

$k(x)=1 \quad \mathrm{f\ddot ur} \quad x\geq +1$,

$0<k(x)<1 \quad \mathrm{f\ddot ur} \quad -1<x<1$.

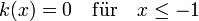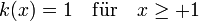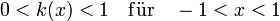Folgerung

Die Zerlegung der Eins ist ein wesentlicher Unterschied zu den analytischen Funktionen, bei denen es keine solche Zerlegung der Eins gibt: Analytische Funktionen sind global bereits durch lokale Daten festgelegt, glatte Funktionen lassen sich aus beliebigen lokalen glatten Daten zusammensetzen.