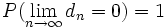Gliwenko-Cantellisches Lemma

Der Gliwenko-Cantelli-Satz, auch Hauptsatz der Statistik oder Fundamentalsatz der Statistik genannt (nach Waleri Iwanowitsch Gliwenko und Francesco Cantelli, 1933), ist ein mathematischer Satz, der besagt, dass die empirische Verteilungsfunktion einer eindimensionalen Stichprobe mit Wahrscheinlichkeit Eins gleichmäßig gegen die tatsächliche Verteilungsfunktion konvergiert.

Formal

Seien X₁,...,X_n unabhängige, identisch verteilte Zufallsvariablen mit der Verteilungsfunktion F.

Sei 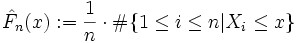$\hat F_n (x) := { 1 \over n } \cdot \# \{ 1 \le i \le n | X_i \le x \}$ die enstsprechende empirische Verteilungsfunktion (hierbei gibt wie üblich das Rautensymbol 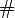$\#$ die Anzahl der Elemente der darauf folgenden Menge an).

Man definiert als größte Abweichung der empirischen Verteilung von der zu Grunde liegenden Verteilung der Zufallsvariablen bezüglich aller Ausprägungen x

$d_n=\sup_x | \hat F_n (x) - F (x) |$.

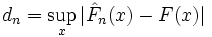Dann gilt, dass die Differenz d_n mit der Wahrscheinlichkeit 1 gegen Null konvergiert:

$P(\lim_{n \to \infty} d_n = 0) = 1$