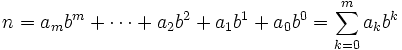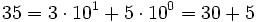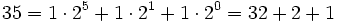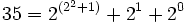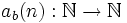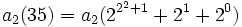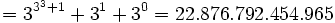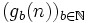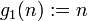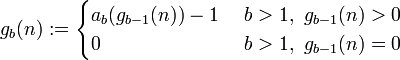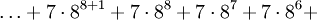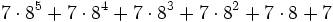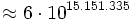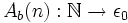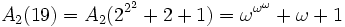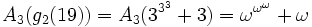Goodsteinfolgen

Goodstein-Folgen sind spezielle Folgen natürlicher Zahlen. Sie spielen eine Rolle in einem mathematischen Satz, dem Satz von Goodstein. Das Besondere an diesem Satz ist, dass er sich zwar mit den Mitteln der Peano-Arithmetik formulieren, aber nicht ausschließlich mit ihnen beweisen lässt. Dies liegt daran, dass die Peano-Arithmetik die natürlichen Zahlen nicht eindeutig modelliert, d.h., sie erlaubt auch andere Modelle als die natürlichen Zahlen, in denen der Satz von Goodstein nicht gilt. Dieser Satz ist ein Beispiel dafür, dass nicht jede unbeweisbare Aussage so kompliziert und „unvorstellbar“ sein muss wie die unbeweisbaren Aussagen im gödelschen Unvollständigkeitssatz.

Der Satz von Goodstein

Der Satz von Goodstein lautet:

Jede Goodstein-Folge mit beliebigem Anfangswert aus den natürlichen Zahlen erreicht in endlich vielen Schritten den Wert null.

Dieser Satz wurde 1944 vom englischen Logiker Reuben Louis Goodstein (1912–1985) bewiesen. Dieser Satz ist innerhalb der Mathematik vor allem deswegen interessant, weil er sich nicht mit den Peano-Axiomen herleiten lässt. Stattdessen verwendet der Beweis Mittel der Mengenlehre, speziell die Theorie der Ordinalzahlen.

Definition der Goodstein-Folgen

Jede natürliche Zahl n kann wie folgt zu einer gegebenen Basis b entwickelt werden:

$n=a_m b^m + \cdots + a_2 b^2 + a_1 b^1 + a_0 b^0 = \sum_{k=0}^{m}a_k b^k$

wobei die a_k Koeffizienten sind, die zwischen 0 und b-1 liegen (siehe Stellenwertsystem).

Zum Beispiel ist "35" die Darstellung einer natürlichen Zahl im Dezimalsystem:

$35 = 3 \cdot 10^1 + 5 \cdot 10^0 = 30 + 5$

Zur Basis 2 lautet die Darstellung

$35 = 1 \cdot 2^5 + 1 \cdot 2^1 + 1 \cdot 2^0 = 32 + 2 + 1$

Diese Darstellung zur Basis b wird nun auf die Exponenten angewendet, und dann auf die Exponenten der Exponenten, solange bis keine Zahl oberhalb der Basis mehr auftritt. Diese Darstellung nennt man die iterierte Darstellung zur Basis b (engl. hereditary base b representation). Für die Zahl 35 ergibt sich diese Darstellung:

$35 = 2^{(2^2 + 1)} + 2^1 + 2^0$

Mit dieser iterierten Darstellung wird die Goodsteinsche Operation "aufblähen" (engl. "bump the base") definiert. Diese ersetzt überall dort, wo in der iterierten Darstellung einer Zahl die Basis b steht, diese durch (b + 1). Diese Abbildung, die die Zahl n zur Basis b iteriert darstellt und dann aufbläht, wird hier als

$a_b(n): \mathbb{N} \to \mathbb{N}$

geschrieben (es gibt in der Literatur viele verschiedene Schreibweisen dafür).

$a_2(35) = a_2(2^{2^2 + 1} + 2^1 + 2^0)\;$

$= 3^{3^3 + 1} + 3^1 + 3^0 = 22.876.792.454.965\;$

Ist nun n eine natürliche Zahl, dann wird die Goodstein-Folge mit Startwert n

$(g_b(n))_{b \in \mathbb{N}}\;$

unter Verwendung dieser Abbildung a_b so definiert:

$g_1(n) := n \;$

$g_b(n) := \begin{cases} a_b(g_{b-1}(n)) - 1 & \ b>1,\ g_{b-1}(n)>0\\ 0 & \ b>1,\ g_{b-1}(n)=0 \end{cases}$

Das zweite Folgenglied wird also berechnet, indem man n zur Basis b = 2 iteriert darstellt,dann aufbläht und von der aufgeblähten Zahl 1 abzieht.

Beispiele

Die Goodstein-Folgen für n=1 bis 3 sind noch recht kurz:

n=1:

g₁(1) = 1

g₂(1) = 0

n=2:

g₁(2) = 2

g₂(2) = a₂(2¹) − 1 = 3¹ − 1 = 2

g₃(2) = a₃(2) − 1 = 2 − 1 = 1

g₄(2) = a₄(1) − 1 = 1 − 1 = 0

n=3:

g₁(3) = 3

g₂(3) = a₂(2¹ + 1) − 1 = 3¹ + 1 − 1 = 3

g₃(3) = a₃(3¹) − 1 = 4¹ − 1 = 3

$g_4(3) = a_4(3 \cdot 4^0) - 1 = 3 \cdot 5^0 - 1 = 2$

$g_5(3) = a_5(2 \cdot 5^0) - 1 = 2 \cdot 6^0 - 1 = 1$

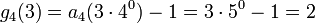
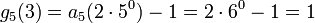
g₆(3) = a₆(6⁰) − 1 = 7⁰ − 1 = 0

Man beachte, dass hier ab b=4 die Erhöhung der Basis keine Auswirkung mehr hat, weil die Zahl dann kleiner als die Basis ist, sie ist bgzl. dieser Basis sozusagen "einstellig".

n=4:

g₁(4) = 4

g₂(4) = a₂(2²) − 1 = 3³ − 1 = 26

$g_3(4) = a_3(2 \cdot 3^2 + 2 \cdot 3^1 + 2) - 1 = 2 \cdot 4^2 + 2 \cdot 4^1 + 2 - 1 = 41$

$g_4(4), \ldots, g_{10}(4) = 60, 83, 109, 139, 173, 211, 253\;$

$g_{11}(4) = a_{11}(2 \cdot 11^2 + 11^1) - 1 = 2 \cdot 12^2 + 12^1 - 1 = 299$

$g_{12}(4) = a_{12}(2 \cdot 12^2 + 11) - 1 = 2 \cdot 13^2 + 11 - 1 = 348$

...

$g_{100}(4) = 101^2 + 21\cdot 101 + 90 = 12.412$

...

$g_{1000}(4) = 1001^2 + 18\cdot 1001 + 534 = 1.020.533$

...

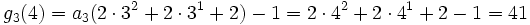
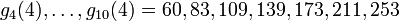
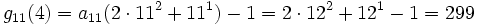
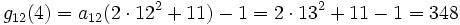
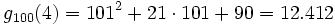
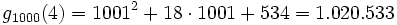
Diese Folge steigt noch recht lange an, bis zur Basis 3 · 2^402.653.209, bleibt dann noch einmal doppelt solange konstant, und fällt dann ab, bis bei der Basis 3 · 2^402.653.211 - 1 der Wert 0 erreicht wird. Die Anzahl der benötigten Schritte ist hier also selbst eine Zahl mit mehr als 121 Millionen Dezimalstellen.

Einen Eindruck davon, wie schnell Goodstein-Folgen wachsen können, liefern größere Werte von n.

n=19:

g₁(19) = 19

$g_2(19) = a_2(2^{2^2} + 2 + 1) - 1 = 3^{3^3} + 3 = 7.625.597.484.990$

$g_3(19) = 4^{4^4} + 3 \approx 1{,}3 \cdot 10^{154}$

$g_4(19) = 5^{5^5} + 2 \approx 1{,}8 \cdot 10^{2184}$

$g_5(19) = 6^{6^6} + 1 \approx 2{,}6 \cdot 10^{36.305}$

$g_6(19) = 7^{7^7} \approx 3{,}8 \cdot 10^{695.974}$

$g_7(19) = 8^{8^8} - 1 = 7\cdot 8^{(7\cdot 8^7 + 7\cdot 8^6 + 7\cdot 8^5 + 7\cdot 8^4 + 7\cdot 8^3 + 7\cdot 8^2 + 7\cdot 8 + 7)}+$

$\ldots+7\cdot 8^{8+1} + 7\cdot 8^8 + 7\cdot 8^7 + 7\cdot 8^6 +$

$7\cdot 8^5 + 7\cdot 8^4 + 7\cdot 8^3 + 7\cdot 8^2 + 7\cdot 8 + 7$

$\approx 6\cdot 10^{15.151.335}$

...

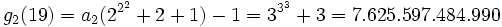
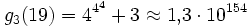
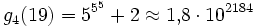
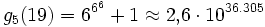
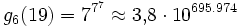
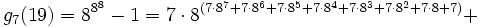
Trotz des rasanten Wachstums dieser Folgen behauptet nun der Satz von Goodstein, dass alle diese Folgen irgendwann wieder fallen und bei 0 enden.

Beweis des Satzes von Goodstein

Der Satz von Kirby und Paris besagt, dass der Satz von Goodstein nicht mit Mitteln der Peano-Arithmetik beweisbar ist, insbesondere kann man ihn nicht durch vollständige Induktion beweisen. Man benötigt also ein mächtigeres Werkzeug: die Ordinalzahlen.

Die Theorie der Ordinalzahlen erweitert die natürlichen Zahlen um Größen, die größer als alle natürlichen Zahlen sind. Die kleinste unendliche Ordinalzahl wird ω (kleiner griech. Buchstabe omega) genannt. Ordinalzahlen kann man addieren, multiplizieren und potenzieren, jedoch gelten einige Rechenregeln der natürlichen Zahlen nicht für Ordinalzahlen (z. B. ist ω+1 ≠ 1+ω = ω). Ordinalzahlen sind der Größe nach geordnet (sie haben eine totale Ordnung), die drei genannten Rechenarten sind monoton in allen Argumenten, und die Ordinalzahlen sind wohlgeordnet, d. h., es gibt keine streng monoton fallende unendliche Folge von Ordinalzahlen.

Wir ordnen nun jeder natürlichen Zahl n eine Ordinalzahl zu, indem wir n zur Basis b iteriert darstellen und dann jedes b durch ω ersetzen. Die so entstehenden Ordinalzahlen lassen sich durch eine endliche Folge von Additionen, Multiplikationen und Potenzierungen aus ω und natürlichen Zahlen gewinnen; die Menge der so darstellbaren Ordinalzahlen heißt ε₀ (diese Menge ist die kleinste Ordinalzahl, die nicht auf diese Weise darstellbar ist). Wir haben also eine Abbildung

$A_b(n): \mathbb{N} \to \epsilon_0$

(auch hier gibt es in der Literatur unterschiedliche Schreibweisen).

Es ist z. B.

$A_2(19) = A_2(2^{2^2} + 2 + 1) = \omega^{\omega^\omega} + \omega + 1$

$A_3(g_2(19)) = A_3(3^{3^3} + 3) = \omega^{\omega^\omega} + \omega$

Ist n kleiner als b, dann ist A_b(n) eine endliche Ordinalzahl, z. B. ist

A₅(3) = 3

Das Aufblähen hat keine Auswirkung auf die Ordinalzahl, denn es spielt keine Rolle, ob man in der iterierten Darstellung gleich jedes b durch ω ersetzt, oder erst jedes b durch (b + 1) und dann jedes (b + 1) durch ω, es gilt also

A_{b + 1}(a_b(n)) = A_b(n)

Die Subtraktion von 1 hat jedoch Auswirkungen auf die Ordinalzahl: Diese wird reduziert.

Beispielsweise gilt

A₅(a₄(4⁴ + 4)) = A₅(5⁵ + 5) = ω^ω + ω

A₅(a₄(4⁴ + 4) − 1) = A₅(5⁵ + 4) = ω^ω + 4

Der Goodstein-Folge 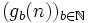$(g_b(n))_{b \in \mathbb{N}}$ ordnen wir nun eine Folge von Ordinalzahlen 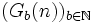$(G_b(n))_{b \in \mathbb{N}}$ so zu:

G_b(n): = A_{b + 1}(g_b(n))

Diese Folge wird oft die "Parallelfolge" (engl. "parallel sequence") genannt.

Diese Folge von Ordinalzahlen ist streng monoton fallend, muss also nach endlich vielen Schritten bei 0 enden (Ordinalzahlen haben eine Wohlordnung). Da 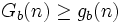$G_b(n) \geq g_b(n)$ für alle n und b gilt, endet also auch die Goodstein-Folge nach endlich vielen Schritten.

Der Satz von Goodstein macht keine Aussage darüber, nach wie vielen Schritten eine Goodstein-Folge endet; er ist also ein reiner Existenzsatz:

Zu jedem natürlichen n existiert ein b, so dass g_b(n) = 0 ist.

Unabhängigkeit von der Peano-Arithmetik

Während der Beweis des Satzes von Goodstein noch relativ einfach ist (sofern man mit der Theorie der Ordinalzahlen vertraut ist), ist die Behauptung, dass dieser Satz nicht allein mit der Peano-Arithmetik beweisbar ist, deutlich schwieriger zu beweisen. Dies gelang Laurie Kirby und Jeff Paris 1982. Der nach ihnen benannte Satz von Kirby und Paris verwendet ein so genanntes Nichtstandardmodell der Peano-Arithmetik.

Literatur

• R. Goodstein: On the restricted ordinal theorem. In: Journal of Symbolic Logic. Band 9, 1944, Seiten 33-41.
• Laurie Kirby, Jeff Paris: Accessible independence results for Peano arithemtic. In: Bulletin of the London Math. Soc. Band 14, 1982, Seiten 285-293.
• Dehornoy: Braucht die Arithmetik das Unendliche? In: Spektrum Sonderheft Das Unendliche.

Weblinks

• Eine Abhandlung über den Beweis des Satzes von Goodstein und seine Unabhängigkeit von den Peano-Axiomen (englisch)