Stellenwertsystem

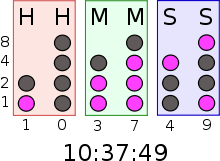Eine binäre Uhr kann Leuchtdioden benutzen, um binäre Werte darzustellen. Im obigen Bild ist jede Spalte von Leuchtdioden eine BCD-Codierung der traditionell sexagesimalen Zeitdarstellung.

Ein Stellenwertsystem, Positionssystem oder polyadisches Zahlensystem ist ein Zahlensystem, das im Vergleich zu Additionssystemen mit einem endlichen Vorrat von Symbolen (meist Ziffern oder Zahlzeichen genannt) beliebig große Zahlen darstellen kann. In diesem Zusammenhang wird auch oft von der b-adischen Darstellung von Zahlen (nicht zu verwechseln mit p-adischen Zahlen) gesprochen, wobei die Variable b für die Anzahl der Symbole steht. Der Wert von b wird auch als Basis oder Grundzahl bezeichnet. Jede ganze Zahl $b \geq 2$ ist als Basis für ein Stellenwertsystem geeignet.

Beispiele für Stellenwertsysteme sind das im Alltag gewöhnlich gebrauchte Dezimalsystem (dekadisches System mit der Grundzahl 10) oder das in der Datenverarbeitung häufig verwendete Dualsystem (dyadisches System mit der Grundzahl 2), das Oktalsystem (mit der Grundzahl 8), das Hexadezimalsystem (mit der Grundzahl 16) sowie das Sexagesimalsystem (mit der Grundzahl 60). Ein Beispiel für ein Zahlensystem, das kein Stellenwertsystem ist, ist das der römischen Ziffern. Es handelt sich dabei um ein Additionssystem.

Es gibt zwei unterschiedliche Arten, die Zifferndarstellung einer Zahl zu betrachten:

• einerseits als Folge von Symbolen, also aufgefasst als Wörter einer formalen Sprache,
• andererseits als Folge von Zahlen, die diesen Symbolen entsprechen.

Durch die Zuordnung zwischen Symbolen und Zahlen stehen die beiden Sichtweisen in enger Beziehung. Für mathematische Anwendungen wie zum Beispiel bei Teilbarkeitsregeln wird meist die zweite Möglichkeit gewählt.

Geschichte

Dieses System stammt ursprünglich aus Indien. Adam Ries verbreitete mit seinen Werken das schriftliche Rechnen mit dem Stellenwertsystem im deutschsprachigen Raum.

Grundlagen

Die b-adische Darstellung einer Zahl verwendet genau b verschiedene Ziffern. Jeder der b Ziffern wird eineindeutig (bijektiv) eine der Zahlen von 0 bis b − 1 zugeordnet. Zur Unterscheidung sind im Folgenden Ziffersymbole stets fett und ihre zugehörigen Zahlenwerte normal gedruckt.

Beispiele:

• Im Dualsystem mit b = 2 werden gewöhnlich die Ziffern 0 und 1 verwendet und ihnen die Zahlen 0 und 1 zugeordnet.
• Im Dezimalsystem ist b = 10 und es werden gewöhnlich die 10 Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9 verwendet und diesen (in dieser Reihenfolge) die Zahlen 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 zugeordnet.

Für b < 10 werden gewöhnlich die ersten b Ziffern wie im Dezimalsystem verwendet.

Für b > 10 kommen gewöhnlich zusätzlich zu den Ziffern des Dezimalsystems Buchstaben als Ziffern zum Einsatz. Beispielsweise werden im Hexadezimalsystem mit b = 16 zusätzlich die Ziffern A, B, C, D, E und F verwendet und diesen (wieder in dieser Reihenfolge) die Zahlen 10, 11, 12, 13, 14 und 15 zugeordnet.

Darstellungen verschiedener Zahlenmengen

Darstellung natürlicher Zahlen

Natürliche Zahlen werden in der b-adischen Darstellung durch eine (endliche) Folge

$a_0, a_1, a_2, \ldots, a_n$

von Ziffern a_i dargestellt. Dabei wird die Folge aber nicht wie eben gezeigt von links nach rechts und durch Komma getrennt, sondern von rechts nach links und ohne Komma dargestellt, also:

$a_n \ldots a_2 a_1 a_0$

Der Folge wird nun die Zahl

$\sum_{i=0} ^{n} a_i \cdot b^i = a_0 + a_1 \cdot b + a_2 \cdot b^2 + ... + a_n \cdot b^n$

zugeordnet.

Es lässt sich zeigen, dass zu jeder natürlichen Zahl x eine Folge von Ziffern existiert, deren zugeordneter Wert x ist. Im allgemeinen gibt es sogar mehrere Folgen. Es genügt dazu beliebig oft die Ziffer 0 =0 anzuhängen (das heißt in der üblichen Schreibweise voranstellen). Werden Folgen verboten, die mit der Ziffer 0 enden (in der üblichen Schreibweise also solche mit führender 0), so lässt sich zeigen, dass diese Zuordnung sogar eineindeutig ist, das heißt zu jeder natürlichen Zahl x existiert genau eine Folge, deren zugeordneter Wert x ist. Entgegen diesem Verbot wird der Zahl 0 nicht die leere Folge (also die endliche Folge ohne ein einziges Folgenglied) zugeordnet, sondern die Folge, die aus genau einem Folgenglied besteht, nämlich der Ziffer, der der Wert 0 zugeordnet wird (also 0), um diese Zahl überhaupt darstellen zu können.

Als Beispiel betrachten wir die Ziffernfolge 4C3 im Hexadezimalsystem (b = 16):

a₀ ist hier 3, a₁ ist hier C und a₂ ist 4. Ferner ist 3 = 3, C = 12 und 4 = 4. Also repräsentiert die Folge 4C3 die Zahl

$a_0 + a_1 \cdot b + a_2 \cdot b^2 = 3 + 12 \cdot 16 + 4 \cdot 16^2 = 3 + 192 + 1024 = 1219.$

Entsprechend repräsentiert die Folge 1010011 im Dualsystem (b = 2) die Zahl

$1 \cdot 2^0 + 1 \cdot 2^1 + 0 \cdot 2^2 + 0 \cdot 2^3 + 1 \cdot 2^4 + 0 \cdot 2^5 + 1 \cdot 2^6 = 1 + 2 + 16 + 64 = 83.$

Im Dezimalsystem (b = 10) steht 3072 für:

$2 \cdot 10^0 + 7 \cdot 10^1 + 0 \cdot 10^2 + 3 \cdot 10^3 = 3072.$

Darstellung ganzer Zahlen

Ganze Zahlen werden wie natürliche Zahlen durch endliche Ziffernfolgen dargestellt, mit dem Unterschied, dass negativen Zahlen ein Minuszeichen („-“) als Symbol vorangestellt wird. Darstellungen von Zahlen verschieden von 0, denen kein Minuszeichen vorangestellt wird, werden als positive Zahlen interpretiert. Manchmal möchte man diese Positivität jedoch besonders hervorheben. In solchen Fällen wird in der Darstellung ein Pluszeichen („+“) vorangestellt.

Darstellung rationaler Zahlen

Auch rationale Zahlen lassen sich b-adisch darstellen. Wie im Dezimalsystem wird hierbei mit einem Trennzeichen der ganzzahlige vom gebrochenen Teil abgetrennt. Im deutschsprachigen Raum (ausgenommen Schweiz) ist hierfür das Komma »,«, im englischsprachigen Raum dagegen der Punkt ».« gebräuchlich. Die Werte der Ziffern hinter dem Trennzeichen werden mit b^-i multipliziert, wobei i die Position hinter dem Komma angibt.

Zum Beispiel wird die rationale Zahl 1+3/8 = 1,375 im 2-adischen Stellenwertsystem durch die Ziffernfolge 1,011 dargestellt. In der Tat ist

$1\cdot 2^0 + 0\cdot 2^{-1} + 1\cdot 2^{-2} + 1\cdot 2^{-3} = 1 + 0/2 + 1/4 + 1/8 = 1+3/8.$

Es kann dabei vorkommen, dass zur Darstellung eine unendliche, aber periodische Folge von Nachkommastellen benötigt wird. Gewöhnlich wird diese Periode dann durch eine über die periodischen Ziffern gezogene Linie gekennzeichnet und so eine endliche Darstellung möglich.

Während die Zahl 1/5 = 0,2 im Dezimalsystem die endliche Symbolfolge 0,2 hat, ist ihre Darstellung im Dualsystem periodisch:

$0{,}00110011\ldots = 0{,}\overline{0011},$

Dagegen bezeichnet die Ziffernfolge 0,1 im 3-adischen (triadischen) System die rationale Zahl 1·3^-1 = 1/3, die im Dezimalsystem einer unendlichen periodischen Ziffernfolge 0,333... entspricht.

Allgemein gilt, dass ein gekürzter Bruch genau dann eine endliche b-adische Darstellung hat, wenn alle Primfaktoren seines Nenners auch Primfaktoren von b sind. (Für eine endliche Darstellung im Dezimalsystem muss der gekürzte Nenner also ein Produkt der Zahlen Zwei und Fünf sein.)

Man beachte, dass die Zifferndarstellung mancher rationaler Zahlen nicht mehr eindeutig ist. So bezeichnen die Ziffernfolgen 1, 1,0, 1,000... und 0,999... im Dezimalsystem dieselbe rationale (sogar natürliche) Zahl 1. Während die ersten drei Darstellungen sofort als gleichwertig erkennbar sind, wird eine geometrische Reihe benötigt, um

$0{,}999\ldots = \sum_{i=1}^\infty 9\cdot 10^{-i} = 9\cdot \sum_{i=1}^\infty 10^{-i} = 9\cdot \frac{1}{9} = 1$

nachzuweisen. Der „alltagstaugliche“ Beweis

$1 = \frac{9}{9} = 9 \cdot \frac{1}{9} = 9 \cdot 0{,}111\ldots = 0{,}999\ldots$

macht von dieser unendlichen Reihe Gebrauch. Dieses Phänomen tritt bei jeder Basis b auf, denn die Ziffernfolge

$0{,}0\mathbf{nnn}\ldots=0{,}0\overline{\mathbf{n}}$

hat den Wert $\tfrac1b$, wobei $\mathbf{n}$ die Ziffer b − 1 bezeichnet. Den Wert $\tfrac1b$ hat aber auch die Ziffernfolge

$0{,}1\mathbf{000}\ldots=0{,}1\overline{\mathbf{0}}$.

Normalerweise sind Missverständnisse nicht zu befürchten, so dass man beide Darstellungen zulassen kann. Eindeutigkeit ist jedoch z. B. bei der Z-Kurve gefordert, die $Z \colon \R^2 \to \R^1$ injektiv abbildet und bei der abwechselnd 2 b-Ziffernfolgen in 1 gepresst werden. Die Unstetigkeitsstellen der Funktion Z sind übrigens genau die Argumente, die eine endliche b-adische Darstellung haben.

Die Länge der Periode einer rationalen Zahl mit dem gekürzten Nenner $n=c \cdot d$, mit natürlichen Zahlen c,d und dem (größter gemeinsamer Teiler) $\operatorname{ggT}(b,d)=1$, in der b-adischen Darstellung ist 0 für d = 1 („endliche“ Darstellung), andernfalls der kleinste Exponent e > 0, für den d Teiler von b^e − 1 ist.

Darstellung reeller Zahlen

Die Darstellung reeller Zahlen erfolgt prinzipiell genauso wie die von rationalen Zahlen durch b-adische Entwicklung. Bei rationalen Zahlen liefert diese eine abbrechende oder eine unendliche periodische Ziffernfolge.

Die b-adische Entwicklung einer irrationalen Zahl (wie π oder $\sqrt{2}$) liefert dagegen stets eine unendliche nichtperiodische Ziffernfolge. Durch Verlängerung des Nachkommaanteils ist eine beliebig genaue Annäherung an die irrationale Zahl möglich.

Wie bei den rationalen Zahlen mit unendlich periodischer Ziffernfolge ist eine endliche Darstellung für irrationale Zahlen durch Einführung neuer Symbole möglich, so wie dies hier für die Beispiele π und $\sqrt{2}$ geschehen ist.

Trotzdem kann selbst mit beliebig, aber endlich vielen zusätzlichen Zeichen nicht jede reelle Zahl als endliche Zeichenfolge dargestellt werden. Dies liegt daran, dass die Menge der reellen Zahlen überabzählbar, die Menge aller endlichen Darstellungen mit endlichem Zeichenvorrat aber nur abzählbar ist.

Wenn aber unter der „Darstellung“ einer reellen Zahl die bei der b-adischen Entwicklung entstehende Ziffernfolge verstanden wird, dann ist jede reelle Zahl als (ggf. unendlicher) b-adischer Bruch darstellbar, auch wenn nicht jeder solche Bruch tatsächlich aufschreibbar ist.

Formelsammlung für Ziffern und Operationen mit Ziffern

Die letzte Ziffer der b-adischen Darstellung einer natürlichen Zahl n ist der Rest von n bei Division durch b. Dieser Rest ist auch durch den Ausdruck

$n-b\left\lfloor\frac nb\right\rfloor$

gegeben; dabei bezeichnet $\lfloor{\cdot}\rfloor$ die Gaußklammer. Allgemeiner ist die durch die letzten k Ziffern von n gebildete Zahl der Rest von n bei Division durch b^k.

Die k-te Ziffer (von rechts mit null beginnend gezählt) einer positiven reellen Zahl x ist

$\left\lfloor\frac x{b^k}\right\rfloor-b\left\lfloor\frac x{b^{k+1}}\right\rfloor;$

für negative k ergibt sich die entsprechende Nachkommastelle.

Die Anzahl der Ziffern der b-adischen Darstellung einer natürlichen Zahl n ist

$\lfloor\log_bn\rfloor+1.$

Hängt man an eine Zahl n in b-adischer Darstellung eine Ziffer z an, so erhält man die b-adische Darstellung der Zahl bn + z.

Gebräuchliche Basen

• Das bekannteste und verbreitetste Stellenwertsystem ist das Dezimalsystem (oder Zehner-System) mit Basis 10 und den Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9. Das Dezimalsystem stammt ursprünglich aus Indien. Der persische Mathematiker Muhammad ibn Musa al-Chwarizmi verwendete es in seinem Arithmetikbuch, das er im 8. Jahrhundert schrieb. Bereits im 10. Jahrhundert wurde das System in Europa eingeführt, damals noch ohne Null. Durchsetzen konnte es sich jedoch erst im 12. Jahrhundert mit der Übersetzung des genannten Arithmetikbuchs ins Lateinische.
• Im 17. Jahrhundert führte der Mathematiker Gottfried Wilhelm Leibniz mit der Dyadik das Dualsystem (ein binäres Zahlensystem) ein, also das Stellenwertsystem mit der Basis 2 und den Ziffern 0 und 1. Dieses wird vor allem in der Informationstechnik verwendet, da deren Logik allein auf Bits, welche entweder wahr oder falsch bzw. 1 oder 0 sind, ausgerichtet ist.
• Da Binärdarstellungen großer Zahlen unübersichtlich lang sind, wird an ihrer Stelle oft das Hexadezimal- oder Sedezimalsystem verwendet, das mit der Basis 16 (und den Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E und F) arbeitet. Hexadezimale und binäre Darstellung lassen sich leicht ineinander umwandeln, da 4 Stellen (= 1 Nibble) einer binären Zahl gerade einer Stelle einer hexadezimalen Zahl entsprechen.
• Mit BCD-Zahlen hat man ein System der Computertechnik, das bei 16-wertigen Gruppen nur 10 Werte tatsächlich nutzt. Es handelt sich somit um ein Dezimalsystem, das aber an das Binärsystem durch Nutzung der vom hexadezimalen her bekannten Stellen-Gliederung angepasst wurde.
• In der Computertechnik wird neben dem Binär- und Hexadezimalsystem auch das Oktalsystem zur Basis 8 (Ziffern 0–7, 3 Binärstellen = 1 Oktalstelle) verwendet. Diese Verwendung nimmt aber immer mehr ab, da sich die heute üblichen Wortlängen von 8 Bit nicht in eine ganze Anzahl von Stellen im Oktalsystem umwandeln lassen.
• Ebenfalls Verwendung findet die Basis 64 bei Base64 (mit ungewohnter Symbolreihenfolge), sowie gelegentlich die Basis 32 mit den Ziffern 0..9 und a..v unter der Bezeichnung Radix32.
• Das Vigesimalsystem verwendet als Basis die Zahl Zwanzig. Es dürfte entstanden sein, weil zum Zählen neben den Fingern auch die Zehen benutzt wurden und war u.a. in fast allen mesoamerikanischen Kulturen gebräuchlich. Das am weitesten entwickelte System dieser Art wurde von den Mayas in der Klassischen Periode für astronomische Berechnungen sowie zur Darstellung von Kalenderdaten verwendet. Es handelte sich um ein Positionssystem »mit einem Sprung«, weil an der dritten Position nur die Ziffern von 1 bis 18 auftreten, um so als maximale Zahl 360 (annähernde Länge des Sonnenjahres) zu erreichen. Die Mayas kannten und benutzten die Null und verwendeten anders als die meisten ihrer mesoamerikanischen Nachbarn neben dem in der Region allgemein üblichen zyklischen Ritual- sowie einem ebenfalls zyklischen Sonnenkalender auch eine lineare »Lange Zählung (Long Count)«, mit dem die Anzahl der Tage, die seit einem mythischen Anfang vergangen waren, angegeben wurden.
• Das Duodezimalsystem hat als Basis die 12. Wir finden es in der Rechnung mit Dutzend und Gros und im angelsächsischen Maßsystem (1 Shilling = 12 Pence) (siehe auch Alte Maße und Gewichte). Auch die Stundenzählung hat in diesem System ihren Ursprung. In vielen polytheistischen Religionen gab es 12 Hauptgötter, die sich z. B. im alten Ägypten in drei oberste Götter und 3*3 zugeordnete Götter aufteilten. (Die Drei galt als perfekte Zahl; siehe auch Dreifaltigkeit).
• Die Babylonier benutzten ein Zahlensystem mit der Basis 60 (Sexagesimalsystem; siehe auch Geschichte von Maßen und Gewichten).
• In Bantusprachen sind die Namen der Zahlen 6, 7, 8 und 9 oft Fremdwörter oder als 5+1, 5+2, 5+3, 5+4 verstehbar, was auf ein Zahlensystem zur Basis 5 hinweist.

  Zum Beispiel:
  Swahili: 1=moja, 2=mbili, 3=tatu, 4=nne, 5=tano, 6=sita, 7=saba, 8=nane, 9=kenda (Arabisch: 6=sitta, 7=saba'a)
  Tshitschewa: 1=modzi, 2=wiri, 3=tatu, 4=nai, 5=sanu, 6=sanu ndi-modzi, 7=sanu ndi-wiri, 8=sanu ndi-tatu, 9=sanu ndi-nai
  

Besonders ausgeprägt ist das Quinärsystem bei den südamerikanischen Betoya: 1=tey, 2=cayapa, 3=tozumba, 4=cajezea, 5=teente, 10=caya ente, 15=tozumba-ente, 20=caesea ente.^[1]

• Das Senärsystem eignet sich zum Zählen bis fünfunddreißig mit 2·5 Fingern. Sprachliche Spuren eines solchen Systems sind sehr selten (beispielsweise Bretonisch 18 = triouec'h, etwa „3 6er“)^[1]
• Die Indianer Südamerikas verwendeten Zahlensysteme zur Basis 4, 8 oder 16, da sie mit Händen und Füßen rechneten, jedoch die Daumen dabei nicht einbezogen.
• Die frühere Vermutung, die Maori benützten ein System zur Basis 11, gilt mittlerweile als überholt.^[1] Einige Völker benutzen das System zur Basis 18.
• Ein zu erwartendes Zahlensystem zur Basis fünf bei Völkern, die nur eine Hand zum Zählen benutzen, wurde bisher nirgendwo entdeckt. Allerdings wurden ab ca. 1100 v. Chr. im indo-chinesischen Raum Rechentafeln Abakus (Rechentafel) benutzt, die dem Unärsystem zugrunde liegen. Aber siehe oben zum Unärsystem in Fünfer-Blöcken, das allerdings ein Additionsystem darstellt.

Konvertierungen

Manchmal benötigt man Konvertierungen zwischen Stellenwertsystemen. Ist das Dezimalsystem nicht beteiligt, kann man es als Zwischenwert verwenden. Die nachfolgenden Berechnungen können auch mit Hilfe eines Taschenrechners durchgeführt werden, bei dem in der Regel die Zahlenein- und ausgabe nur im Dezimalsystem geschieht.

Beispiel 1: Umwandlung einer Darstellung zur Basis 10 in eine Darstellung zur Basis 5

Bezüglich des Zehnersystems habe eine Zahl die Darstellung 47. Gesucht ist die Darstellung dieser Zahl im Fünfersystem.

Um diese Darstellung zu erhalten, dividiert man die gegebene Darstellung schrittweise durch die neue Basis 5. Die verbleibenden Reste liefern die Darstellung zur Basis 5. Dabei entspricht der erste Rest der niedrigstwertigen Ziffer der gesuchten neuen Darstellung (in unserem Fall also der Stelle 5⁰), der zweite Rest entspricht der zweitniedrigstwertigen Ziffer (also der Stelle 5¹) usw. Die zugehörige Rechnung dazu lautet demnach:

• 47 geteilt durch 5 ergibt 9 Rest 2 (entspricht der Ziffer zur Stelle 5⁰ im Ergebnis)
•   9 geteilt durch 5 ergibt 1 Rest 4 (entspricht der Ziffer zur Stelle 5¹ im Ergebnis)
•   1 geteilt durch 5 ergibt 0 Rest 1 (entspricht der Ziffer zur Stelle 5² im Ergebnis)

Als Darstellung der gegebenen Zahl im Fünfersystem erhalten wir somit 142. Die Umwandlung in andere Stellenwertsysteme erfolgt analog.

Beispiel 2: Umwandlung einer Darstellung zur Basis 5 in eine Darstellung zur Basis 10

Bezüglich des Fünfersystems habe eine Zahl die Darstellung 142. Gesucht ist die Darstellung dieser Zahl im Zehnersystem.

Um diese Darstellung zu erhalten, multipliziert man die Ziffern der gegebene Darstellung jeweils mit der jeweiligen „Wertigkeit“ der Stelle und addiert die Ergebnisse auf. Die zugehörige Rechnung dazu lautet demnach:

• 2 mal 5⁰ ergibt 2
• 4 mal 5¹ ergibt 20
• 1 mal 5² ergibt 25

Als Darstellung der gegebenen Zahl im Dezimalsystem erhalten wir somit 2 + 20 + 25 = 47, was auch der Ausgangsdarstellung entspricht. Die Umwandlung in andere Stellenwertsysteme erfolgt analog.

Beispiel 3: Nachkommastellen

Bezüglich des Zehnersystems habe eine Zahl die Darstellung 0,1. Gesucht ist die Darstellung dieser Zahl im Dualsystem.

Hierzu wird der Nachkommaanteil wiederholt mit der Basis des Zielsystems multipliziert. Tritt dabei ein Wert größer 1 auf, wird dessen ganzzahliger Anteil der Reihe der Nachkommastellen hinzugefügt, andernfalls wird eine 0 den Nachkommastellen hinzugefügt. Tritt eine ganze Zahl als Multiplikationsergebnis auf, ist der Nachkommabetrag vollständig bestimmt, oft wird jedoch auch eine Periode auftreten.

Die zugehörige Rechnung dazu lautet demnach:

• 0,1 mal 2 ergibt 0,2 , die erste Nachkommastelle ist also die 0
• 0,2 mal 2 ergibt 0,4 , die zweite Nachkommastelle ist also die 0
• 0,4 mal 2 ergibt 0,8 , die dritte Nachkommastelle ist also die 0
• 0,8 mal 2 ergibt 1,6 , die vierte Nachkommastelle ist also die 1
• 0,6 mal 2 ergibt 1,2 , die fünfte Nachkommastelle ist also die 1
• 0,2 mal 2 (muss nicht mehr ausgeführt werden, da eine Periode aufgetreten ist)

Als Ergebnis erhalten wird somit 0,0001100110011 ...

Verallgemeinerungen

Die Basis b muss nicht notwendigerweise eine natürliche Zahl sein. Sämtliche komplexen Zahlen mit Betrag größer 1 können als Basis eines Stellenwertsystems verwendet werden. Ebenso sind Zahlensysteme mit gemischten Grundzahlen möglich, so zum Beispiel ein fakultätsbasiertes Zahlensystem.

Für solche verallgemeinerten Stellenwertsysteme gelten einige der hier gemachten Aussagen über die endliche Darstellbarkeit rationaler und reeller Zahlen nicht. Wird zum Beispiel der Goldene Schnitt τ = (1+√5)/2 als Basis verwendet, dann stellt eine endliche Ziffernfolge stets eine ganze Zahl oder eine irrationale Zahl der Form r+s√5 mit rationalen r, s dar (dagegen hat nicht jede solche Zahl eine endliche Darstellung).

Die hier vorgestellten Stellenwertsysteme für die rationalen Zahlen beruhen auf der Konvergenz in bezug auf die Metrik des gewöhnlichen archimedischen Absolutbetrags. Die unendlichen Reihen – die hier immer, und zwar rechts bei den kleinen Potenzen, konvergieren – sind dann reelle Zahlen. Es gibt aber für die rationalen Zahlen auch Metriken, die auf nichtarchimedischen Betragsfunktionen basieren und eine ganz ähnliche Notation mit Basis und Ziffernvorrat gestatten. Die unendlichen Reihen – die auch dort immer, und zwar links bei den großen Potenzen, konvergieren – sind p-adische Zahlen.

Weiterführende Texte

Der Artikel Zahlbasiswechsel beschäftigt sich mit der Umrechnung der Darstellung von Zahlen in verschiedenen Zahlensystemen. Eine Einführung zum Rechnen in Stellenwertsystemen befindet sich im Artikel Arithmetik in Stellenwertsystemen. Der Artikel Teilbarkeit erläutert, wie in der Darstellung von Stellenwertsystemen in bestimmten Fällen erkannt werden kann, ob eine Zahl Teiler einer anderen ist.

Literatur

• Donald Knuth. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89684-2. Pages 65–66 (englisch).

Weblinks

• Online-Umrechner für verschiedene Zahlensysteme (JavaScript)
• Kleines und großes 1x1 in Stellenwertsystemen

Einzelnachweise

1. ↑ ^{a b c} Levi Leonard Conant, The Number Concept (Etext im Project Gutenberg, engl.)

Dieser Artikel wurde in die Liste der lesenswerten Artikel aufgenommen. Vorlage:Lesenswert/Wartung/ohne DatumVorlage:Lesenswert/Wartung/ohne Version