- Graphersetzung
-
Graphersetzungssysteme dienen der formalen Beschreibung der Veränderung von Graphen.
Ein Graphersetzungssystem ist eine Menge M von Graphersetzungsregeln
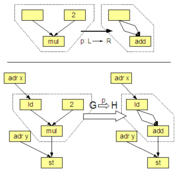
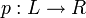 . Eine Graphersetzungsregel p besteht aus dem Mustergraphen L der linken Seite sowie dem Ersetzungsgraphen R der rechten Seite. (zu den möglichen Varianten von Graphen, die in einer Regel auftreten können, siehe Typen von Graphen in der Graphentheorie)
. Eine Graphersetzungsregel p besteht aus dem Mustergraphen L der linken Seite sowie dem Ersetzungsgraphen R der rechten Seite. (zu den möglichen Varianten von Graphen, die in einer Regel auftreten können, siehe Typen von Graphen in der Graphentheorie)Eine Regel p wird in einer direkten Ableitung
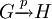 angewandt, G ist der Arbeitsgraph vor der Regelanwendung, H der modifizierte Arbeitsgraph danach. Eine Regelanwendung besteht aus dem Finden einer Instanz von L in G (Pattern Matching, hier: Teilgraphen-Isomorphie) und dem Ersetzen der gefundenen Instanz durch eine Instanz der rechten Seite R. Eine Ableitung ist eine Folge von Regelanwendungen, die einen Ausgangsgraph in einen resultierenden Graphen überführt.
angewandt, G ist der Arbeitsgraph vor der Regelanwendung, H der modifizierte Arbeitsgraph danach. Eine Regelanwendung besteht aus dem Finden einer Instanz von L in G (Pattern Matching, hier: Teilgraphen-Isomorphie) und dem Ersetzen der gefundenen Instanz durch eine Instanz der rechten Seite R. Eine Ableitung ist eine Folge von Regelanwendungen, die einen Ausgangsgraph in einen resultierenden Graphen überführt.Verschiebt sich der Fokus vom Verändern eines gegebenen Graphen hin zum Erzeugen aller, aus einem Startgraphen ableitbarer Graphen, wird von einer Graphgrammatik anstelle eines Graphersetzungssystems und von Produktionen anstelle von Regeln gesprochen. Die Vereinigung der beim systematischen Aufzählen entstehenden Graphen ist die Sprache der Graphgrammatik. Meist werden zudem die Graphelemente in Nichtterminale und Terminale unterschieden, und nur die Nichtterminale ersetzt; unter der Sprache werden dann nur die ableitbaren terminalen Graphen verstanden.
Wohlgeformtheit von Graphen wird häufig über das Enthaltensein in der Sprache einer kontextfreien Graphgrammatik definiert. Ein gegebener Graph kann dann mit einem Graphparser, der berechnet, ob er in der Sprache der Graphgrammatik enthalten ist, auf Wohlgeformtheit geprüft werden, im Erfolgsfall erhält man zudem seine Ableitung(en).
Graphersetzungssysteme können (auch) als eine Verallgemeinerung der Termersetzungssysteme von (Grund-)Termen / deren Bäumen auf Graphen angesehen werden.
Inhaltsverzeichnis
Algebraischer Ansatz
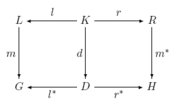
Am meisten Bedeutung bei der Spezifikation von Graphersetzungssystemen hat der algebraische Ansatz erlangt, der mit dem Ziel entwickelt wurde, Chomsky-Grammatiken von Zeichenketten auf Graphen zu verallgemeinern. Das Finden einer Instanz wird durch das Bestimmen eines Passungs-Graphhomomorphismus m von L in G definiert. Bei der Definition des Ersetzens wird das Vorgehen der Konstruktion eines einfachen Pushouts von der Konstruktion eines doppelten Pushouts unterschieden, zu Pushout siehe Kategorientheorie.
Der Zusammenhang zwischen L und R im DPO wird durch einen Klebegraphen K und zwei Graphhomomorphismen
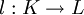 und
und 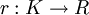 hergestellt. Im Ersetzungsschritt bleiben die Elemente aus K erhalten, die aus
hergestellt. Im Ersetzungsschritt bleiben die Elemente aus K erhalten, die aus 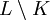 werden gelöscht, die aus
werden gelöscht, die aus 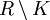 hinzugefügt.
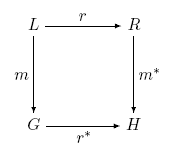
hinzugefügt.Im SPO hingegen wird der Zusammenhang zwischen L und R durch einen partiellen Graphhomomorphismus
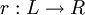 hergestellt. Im Ersetzungsschritt bleiben durch r in Beziehung gesetzte Elemente erhalten, die nicht in Beziehung stehenden aus L werden gelöscht, die nicht in Beziehung stehenden aus R werden hinzufügt.
hergestellt. Im Ersetzungsschritt bleiben durch r in Beziehung gesetzte Elemente erhalten, die nicht in Beziehung stehenden aus L werden gelöscht, die nicht in Beziehung stehenden aus R werden hinzufügt.Beim Ersetzen können zwei Konfliktfälle auftreten:
- Ein zu löschender und ein zu erhaltender Musterknoten werden auf den gleichen Arbeitsgraphknoten abgebildet, es ist nicht klar ob gelöscht oder erhalten werden soll. (Hinweis: Graphhomomorphismus, nicht Graphisomorphismus)
- Ein zu löschender Knoten ist mit nicht im Mustergraphen angegebenen Kanten mit dem restlichen Arbeitsgraphen verbunden, nach alleinigem Löschen des Knotens würden Arbeitsgraphkanten in der Luft hängen.
Die Regelanwendung im DPO wird durch die Konstruktion von zwei Pushouts beschrieben, was in den beiden Konfliktfällen nicht möglich ist, womit die Regel in diesen Fällen nicht angewendet werden kann.
Die Regelanwendung im SPO wird durch die Konstruktion eines Pushouts beschrieben, was bewirkt, dass im 1.Fall Löschen Vorrang vor Erhalten hat, und im 2. Fall in der Luft hängende Kanten gelöscht werden.
Weitere Vorgehensweisen innerhalb des algebraischen Ansatzes stellen der Sesqui-Pushout- sowie der Pullback-Ansatz dar.
Weniger mächtige, kontextfreie Formulierungen von Graphersetzung (außerhalb des algebraischen Ansatzes) sind die Knotenersetzung und die Hyperkantenersetzung. Bei der Knotenersetzung besteht das Muster jeweils nur aus einem Knoten n, der Ersetzungsgraph wird anhand von Verbindungsinstruktionen mit den, vor der Regelanwendung zu der Instanz von n benachbarten(adjazenten) Knoten verbunden. Bei der Hyperkantenersetzung besteht das Muster jeweils nur aus einer Hyperkante e, der Ersetzungsgraph wird mit den, vor der Regelanwendung an der Instanz von e anliegenden(inzidenten) Knoten verklebt.
Anwendung der Graphersetzung
Während die Graphentheorie in der Mathematik Graphen und deren Eigenschaften (wie z.B. Färbbarkeit) betrachtet, und die Graphentheorie in der Theoretischen Informatik ihre Aufmerksamkeit auf Graphersetzungssysteme und deren Eigenschaften (z.B. Konfluenz) richtet, steht für die Praktische Informatik die Bereitstellung von effizienten Graphersetzungssystemen im Vordergrund, die im Rahmen der Angewandten Informatik zum Modellieren von Daten in Form von Graphen und der Spezifikation von Berechnungen auf den Graphen durch Graphersetzungsregeln benutzt werden.
Graphen bieten sich als anschaulicher, mathematisch präziser und ausdrucksstarker Formalismus zur Modellierung von in Beziehung stehender Objekte (Entitäten) an, die Objekte werden dabei in Knoten codiert und die Beziehungen durch Kanten dargestellt. Unterschiedliche Objekte und Beziehungen werden durch unterschiedliche Knoten- und Kantentypen ausgedrückt, in Abhängigkeit von den Typen können die Graphelemente darüber hinaus noch mit Attributen versehen werden. Berechnungen werden in diesem Modell durch Veränderung der Beziehungen zwischen den Objekten dargestellt, aber auch der Veränderung der Attribute. Sie werden durch Graphersetzungsregeln beschrieben.
In der Praxis erfolgt eine, gegenüber dem indeterministischen Konzept des reinen Graphersetzungssystems stärkere, algorithmischere Kontrolle der Regelanwendung, die den Indeterminismus der Regel (welche Regel aus der Regelmenge wird angewendet?) und den Indeterminismus des Ortes (an welcher Stelle im Arbeitsgraphen wird die Regel angewendet?) einschränkt. Dabei kann über Steuerkonstrukte wie Abfolge, Alternative oder Iteration die nächste anzuwendende Regel bestimmt werden (in Abhängigkeit von Erfolg oder Fehlschlag der vorherigen Regelanwendung), oder durch Parameterübergabe zwischen den Regeln das Bearbeiten eines gemeinsamen Ansatzes sichergestellt werden. Es wird dann von "Programmierter Graphersetzung" gesprochen.
Graphen sind in Form von verzeigerten Strukturen (Objekte=Knoten, Referenzen/Zeiger=gerichtete Kanten) in jedem größerem Programm implizit anzutreffen. Sind Objekte, insbesondere Muster von miteinander verbundenen Objekten zu suchen und zu ersetzen, ist ein explizit machen durch die Nutzung eines Graphersetzungssystems lohnend; es kann dann mit kurzen, deklarativen Graphersetzungsregeln gearbeitet werden, anstelle von umfangreichen, handprogrammierten Such- und Ersetzungsunterprogrammen.
Anwendungsbeispiele
- Softwaretechnik: Modellgetriebene Softwareentwicklung mit UML-Graphen, z.B. mit FUJABA
- Übersetzerbau: Optimierungen auf graphbasierten Zwischensprachen, z.B. mit GrGen/Firm
Verfügbare Graphersetzungssysteme
Weblinks
- Algebraic Approaches to Graph Transformation, Part I: Basic Concepts and Double Pushout Approach
- Computing with Graphs and Graph Rewriting
- Graph Transformation in a Nutshell
- Vorlesung Graphersetzungssysteme
- Vorlesung Graphersetzungssysteme
Literatur
- Handbook of Graph Grammars and Computing by Graph Transformations. Volume 1-3. World Scientific Publishing
Wikimedia Foundation.